1. BD-01
ЛАПЛАСЫН ШУУД БА УРВУУ ХУВИРГАЛТ,
ШУГАМАН ДИФФЕРЕНЦИАЛ ТЭГШИТГЭЛИЙН БОДОЛТ

2. Шийдэх асуудал
Анхны нөхцөл нь өгөгдсөн дараах
дифференциал тэгшитгэлийг бод.
Анхны нөхцөл:

3. Шийдэлт
Хэрэглэгдэх илэрхийлэлүүд:

4. Шийдэлт

Шийдэл №1
Өгөгдсөн тэгшитгэлийн хоёр талаас Лапласын хувиргалт
авна:
Анхны
эсвэл
нөхцөлийг орлуулбал:

5. Шийдэлт

Шийдэл №2
дүрс функцийг олно:
эсвэл

6. Шийдэлт

Бие даалт №1
Шийдэл №3
дүрс функцийг энгийн функцүүдийн нийлбэр болгон
задална. Иймд дараах хэлбэрт хувиргаж бичнэ:
энд
эсвэл

7. Шийдэлт

Шийдэл №4
зэрэгтүүдийн коэффициентуудыг харьцуулан бичиж a,
b, c, d үл мэдэгдэх коэффициентуудыг олж
функцийг
нийлбэр хэлбэрт илэрхийлнэ :
эндээс

8. Шийдэлт

Бие даалт №1
Шийдэл №5
функцээс Лапласын урвуу хувиргалт авч
функцийг олно:

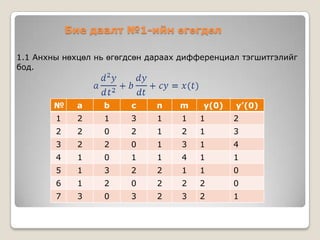
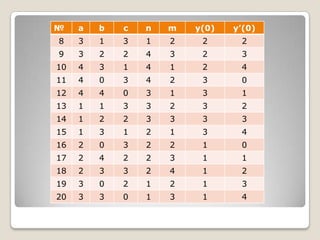
9. Бие даалт №1-ийн өгөгдөл
1.1 Анхны нөхцөл нь өгөгдсөн дараах дифференциал тэгшитгэлийг
бод.
№
a
b
c
n
m
y(0)
y’(0)
1
2
1
3
1
1
1
2
2
2
0
2
1
2
1
3
3
2
2
0
1
3
1
4
4
1
0
1
1
4
1
1
5
1
3
2
2
1
1
0
6
1
2
0
2
2
2
0
7
3
0
3
2
3
2
1

10. №
a
b
c
n
m
y(0)
y’(0)
8
3
1
3
1
2
2
2
9
3
2
2
4
3
2
3
10
4
3
1
4
1
2
4
11
4
0
3
4
2
3
0
12
4
4
0
3
1
3
1
13
1
1
3
3
2
3
2
14
1
2
2
3
3
3
3
15
1
3
1
2
1
3
4
16
2
0
3
2
2
1
0
17
2
4
2
2
3
1
1
18
2
3
3
2
4
1
2
19
3
0
2
1
2
1
3
20
3
3
0
1
3
1
4