1. ОЛОНЛОГ, ЛОГИКИЙН
ЭЛЕМЕНТҮҮД

2. ОЛОНЛОГ БА ТҮҮНИЙ ЭЛЕМЕНТҮҮД









Олонлог гэдэг нь нэгэн ижил шинж тэмдэгтэй юмны
бөөгнөрөл ба олон байхыг шаарддаггүй, ганц обьекттой
олонлог бас нэг ч обьектгүй олонлог байж болдог.
Нэг ч элемент агуулаагүй олонлогийг хоосон олонлог гэж
нэрлээд Ǿ гэж тэмдэглэдэг.
Олонлогийг бүрдүүлж байгаа обьектийг түүний элемент
гэж нэрлээд латин цагаан толгойн жижиг үсгээр
тэмдэглэнэ. Жишээ нь:a,b,c,d…z
Мөн олонлогт ямар нэгэн юм харьяалагдана эсвэл
харьяалагдахгүй гэдгийг тэмдэглэдэг.
Бодлого: 24 гэсэн тоо натурал тоонд харьяалагдах уу?
Бодолт: 24€N
Бодолт: Таван хошуу малын олонлогийн элементүүдийг
нэрлэн бич.
Бодолт: A={таван хошуу малын олонлог}
A={хонь,ямаа,үхэр,адуу,тэмээ}

3. ОЛОНЛОГИЙГ ӨГӨХ АРГУУД





Олонлогийн элемент бүрийн хувьд биелдэг, түүнд
харьяалагдахгүй нэг ч элементийн хувьд биелдэггүй
чанарыг олонлогийн элементийг тодорхойлох шинж чанар
гэнэ. Тухайн олонлогийг элементүүдийнх нь шинж
чанараар өгсөн үед тэмдэглэгээ ашиглан бичдэг. Жишээ
нь:K нь 24 өөс бага натурал тоон олонлог бол K={x/xN ба
x‹24 } гэж бичнэ.
Бодлого: Дараах бичлэгийг уншиж,олонлогийн
элементүүдийг бич.
Бодолт:K={x|2x=x+3} x=3 K={3}
Бодлого: “X олонлог нь нэг оронтой натурал тооны
олонлог” гэсэн шинж чанараар өгсөн олонлогийн
элементийг бич.
Бодолт: X={1,2,3,4,5,6,7,8,9}

4. ОЛОНЛОГ ХООРОНДЫН ХАРЬЦАА
Хэрэв B олонлогийн бүх элемент A олонлогийн
элемент болж байвал B-г A олонлогийн дэд олонлог
гэнэ. Хоосон олонлогийг дурын олонлогийн дэд
олонлог гэж үзнэ. Дурын олонлог өөрийнхөө дэд
олонлог болно.
 A€B ба B€A бол A,B олонлогуудыг тэнцүү
олонлогууд гээд A=B гэж тэмдэглэнэ.
 Хэрэв A олонлог n ширхэг элементтэй бол 2n ширхэг
ялгаатай дэд олонлогтойг баталдаг.
 Бодлого:X={89,67,12,9,79,51}, Y={12,79,9} хоѐр
олонлог өгөгдөв.X,Y олонлогийн огтлолцлыг ол.
Олонлогууд ямар харьцаанд байна вэ?
 Бодолт: X∩Y={12,9} Y€X


5. ОЛОНЛОГУУДЫН ОГТЛОЛЦОЛ

A олонлогт ч B олонлогт ч харьяалагдах элементүүдээс бүрдэх
олонлогийг A ба B олонлогийн огтлолцол гэнэ.A ба B олонлогуудын
огтлолцлыг A∩B гэж тэмдэглэдэг.

A ба B олонлогууд ерөнхий элементгүй үед тэдгээрийн огтлолцлыг
хоосон гээд A∩B=Ǿ

A ба B олонлогийг Эйлерийн дугуйгаар дүрсэлбэл

6. K={16,20,51,62} L={44,88,22,20,16} F={16,44,89,88}
олонлогууд өгөв.Тэдгээрийн хос бүрийн огтлолцлыг
олж, Эйлерийн дугуй ашиглан дүсэл.
 Бодолт: K∩L={16,20} K∩F={16}
L∩F={16,44,88}

K
F
L

7. ОЛОНЛОГУУДЫН НЭГДЭЛ

Зөвхөн A, эсвэл B олонлогт харьяалагдах
элементүүдээс бүрдэх олонлогийг A ба B
олонлогийн нэгдэл гэнэ. A ба B олонлогийн
нэгдлийг AυB гэж тэмдэглэнэ. A ба B олонлогийг
Эйлерийн дугуйгаар дүрсэлбэл:
C
P

8. Бодлого: P,C олонлогуудын нэгдэл M олонлог байг.
M={11,22,33,44,55,66,77,88,99} P={11,33,55,77,99} C
олонлогийн элементүүдийг тоочин бич.
 Бодолт: P∩C=M C={22,44,66,88}
 Олонлогийн нэгдэл ба огтлолцлын чанарууд



Дурын
A
ба
B
олонлогуудын
хувьд:
AυB=BυA, A∩B=B∩A биелнэ. Үүнийг “байр солих’’
чанар гэнэ.Эдгээр чанарыг Эйлерийн дугуйгаар
дүрсэлье. A,B,C олонлогууд хос хосоороо огтлолцсон
A
C
B

9. 










(A∩B)∩C илэрхийлэлд хаалт нь эхлээд A,B олонлогийн
огтлолцол гүйцэтгэхийг илэрхийлнэ.
A,B,C олонлогийн хувьд (AυB)υC=Aυ(BυC) батлагдана.
Олонлогуудын огтлолцол, нэгдлийн хоорондын хамаарлыг
хаалт нээх буюу дистрибутив чанар илэрхийлдэг.Дараах 2
чанарыг авч үзье. Үүнд:
1.Олонлогуудын нэгдлийг олонлогтой огтлолцуулахад хаалт
нээх хууль буюу дистрибутив чанар биелнэ. Өөрөөр хэлбэл
A,B,C дурын олонлогын хувьд (AυB)∩C=(A∩C)υ(B∩C) биелнэ.
2.Олонлогуудын огтлолцлыг олонлогтой нэгтгэхэд хаалт нээх
хууль буюу дистрибутив чанар биелнэ. Өөрөөр хэлбэл A,B,C
дурын олонлогын хувьд (A∩B)υC=(AυC)∩(BυC) биелнэ.
Бодлого:A={а,э,г,л,т,м} B={а,т,з,г,д,ө,ч}
C={т,д,э,х,ц,о,м}
олонлогууд өгөв.Дараах олонлогийн элементүүдийг бич. 1.AυB
2.BυC 3.AυC 4.(AυB)∩C 5.AυBυC 6.(B∩C)υA
Бодолт:1.AυB={а,э,г,л,т,м,з,д,ө,ч}
2.BυC={а,т,з,г,д,ө,ч,э,х,ц,о,м}
3.AυC={а,э,г,л,т,м,д,х,ц,о,}
4.(AυB)∩C={т,д,э,м}
5.AυBυC.={а,э,г,л,т,м,з,д,ө,ч,х,ц,о}
6.(B∩C)υA={т,д,а,э,г,л,т,м}

10. ОЛОНЛОГУУДЫН ЯЛГАВАР, ГҮЙЦЭЭЛТ
олонлогт харьяалагддаг боловч, B олонлогт
харьяалагдаггүй элементүүдээс зөвхөн бүрдэх
олонлогийг A ба B олонлогуудын ялгавар
гэнэ. Үүнийг AB гэж тэмдэглэнэ. B£A байг.
A-д харьяалагддаг ба B-д харьяалагддаггүй
элементүүдээс зөвхөн бүрдэх олонлогийг B
олонлогийн A олонлог хүртэлх гүйцээлт гэнэ.
B олонлогийн A олонлог хүртэлх гүйцээлт
гэдгийг BA Эйлерийн дугуйгаар дүрсэлбэл
A

11. A
B
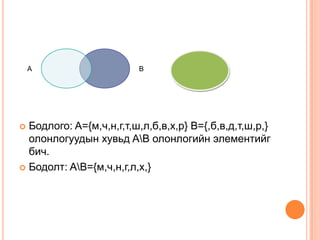
Бодлого: A={м,ч,н,г,т,ш,л,б,в,х,р} B={,б,в,д,т,ш,р,}
олонлогуудын хувьд AB олонлогийн элементийг
бич.
 Бодолт: AB={м,ч,н,г,л,х,}


12. ОЛОНЛОГИЙГ АНГИУДАД ХУВААХ НЬ







Олонлогийн ямарч хуваалт нь тухайн олонлогийн
элементүүдийг дэд олонлогуудад хуваах замаар үүсэж бий
болно. Энэ үед дараах нөхцөлийг хангаж байвал X
олонлогийг X1, X2, X3….Xn ангиудад хуваасан хуваалт
гэнэ. Үүнд:
1.X1,X2,X3….Xn олонлогууд хоорондоо үл огтлолцоно.
2.X1,X2,X3…Xn дэд олонлогуудын нэгдэл X олонлог
байна.
Бодлого: X={1,2,3,4,5,6,7,8,9,10,11,12,13} олонлогоос
дараах дэд олонлогуудад ялга.1.K нь тэгш тоонууд, L нь
сондгой тоонууд
2.A нь нэг оронтой тоонууд B нь хоѐр оронтой
тоонууд
Бодолт: 1. K={2,4,6,8,10,12} L={1,3,5,7,9,11,13}
2.A={1,2,3,3,4,5,6,7,8,9} B={10,11,12,13}

13. ОЛОНЛОГУУДЫН ДЕКАРТ ҮРЖВЭР
A ба B олонлогуудын декарт үржвэр гэж эхний
координат нь A олонлогт харьяалагдах, хоѐр дахь
координат нь B олонлогт харьяалагдах бүх хосоос
бүрдэх олонлогийг хэлнэ. Үүнийг AxB гэж
тэмдэглэнэ.
 1.(AυB)xC=(AxC)υ(BxC)
 2.(AB)xC=(AxB)(BxC)
 Бодлого:A={2,4,7} B={1,3} C={9} олонлогуудын
хувьд 1.A ба B 2.B ба C 3.A ба C олонлогуудын
декарт үржвэрийг ол.
 Бодолт:1.AxB={(2,1);(4,1);(7,1);(2,3);(4,3);(7,3)}
 2.BxC={(1,9);(3,9)}
 3.AxC={(2,9);(4,9);(7,9)}


14. ТӨГСГӨЛӨГ ОЛОНЛОГИЙН НЭГДЭЛ БА
ОГТЛОЛЦЛЫН ЭЛЕМЕНТИЙН ТОО










A олонлог a ширхэг элементтэй, B олонлог b ширхэг элементтэй ба
A,B олонлогууд огтлолцохгүй байвал A ба B олонлогуудын нэгдэл
олонлогийн элементийн тоо a+b байхыг баталдаг. Томьѐолбол:
n(AυB)=n(A)+n(B)=a+b
Харин A ба B олонлог огтлолцож байвал n(AυB)=n(A)+n(B)n(A∩B)
3н элементтэй үед n(AυBυC)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)n(A∩C)
Бодлого:Ангийн 38н оюутнаас 15 нь англи хэл, 13 нь математикийн
сонгонд явдаг. Хоѐр дугуйланд зэрэг явдаг оюутны тоо, болон
зөвхөн нэг дугуйланд явдаг оюутны тоо хэд байж болох вэ?
Бодолт: A-{англи хэлний сонгонд явдаг оюутан}
B-{математикийн сонгонд явдаг оюутан}
n(AυB)=38 n(A)=15 n(B)=13 n(AυB)= n(A)+ n(B)-n(A∩B)
n(A∩B)=10 (хоѐр дугуйланд зэрэг явдаг оюутан)
Зөвхөн англи хэлний дугуйланд явдаг оюутан: 15-10=5 оюутан
Зөвхөн математикийн дугуйланд явдаг оюутан: 13-10=3 оюутан

15. ТӨГСГӨЛӨГ ОЛОНЛОГУУДЫН ДЕКАРТ
ҮРЖВЭРИЙН ЭЛЕМЕНТИЙН ТОО

A олонлогийн элементийн тоо-а, B олонлогийн
элементийн тоо-b, байвал A ба B олонлогуудын
декарт үржвэрийн элементийн тоо axb болно.
n(AxB)=n(A).n(B)=axb

16. УХАГДАХУУНЫ АГУУЛГА БА БАГТААМЖ
,УХАГДАХУУН ХООРОНДЫН ХАРЬЦАА

Нэг нэр томьёогоор тэмдэглэгдэх обьектуудын
олонлогийг ухагдахууны багтаамж гэнэ. Тухайн
ухагдахуунд хамаарагдах обьектын бодит бүх
шинж чанарын олонлогийг ухагдахууны агуулга
гэнэ. Хэрэв A‹B (A≠B) байвал а ухагдахууныг b
ухагдахуунтай хэлбэрийн харьцаанд, харин bухагдахууныг а-ухагдахуунтай төрлийн
харьцаанд оршиж байна гэнэ.

17. УХАГДАХУУНЫ ТОДОРХОЙЛОЛТ
Шинэ нэр томьѐо (эсвэл тэмдэглэгээ)-ний мөн
чанарыг тайлбарласан өгүүлбэрийг тодорхойлолт
гэнэ.
 Тодорхойлогдогч ухагдахуун=Төрөл
ухагдахуун+Хэлбэрийн ялгаа


18. ХЭЛЛЭГ БА ХЭЛЛЭГЖИХ ХЭЛБЭР
Математикт үнэн эсвэл худал утга санааг
илэрхийлсэн хүүрнэх өгүүлбэрийг хэллэг гэнэ.
Хэллэгийг латин цагаан толгойн том үсгээр
тэмдэглэдэг. Үүнд:A,B,C…Z
 Үнэн ба худал байх боломжийг хэллэгийн үнэний
утга гэдэг. Хэллэг бүр эсвэл үнэн, эсвэл худал байх ба
нэгэн зэрэг үнэн, худал байж болохгүй.
 Хувьсагч нь X олонлогоос утгаа авахад хэллэг болох
хувьсагчтай өгүүлбэрийг X олонлогт өгөгдсөн нэг
байрт хэллэгжих хэлбэр гэнэ.
 Логикд <ба>,<эсвэл>,<үг болон ..гүй>,<...гэдэг нь
худал> холбоо үгийг логикийн холбоос гэнэ


19. ХЭЛЛЭГИЙН КОНЪЮНКЦ БА ДИЗЪЮНКЦ
A ба B хэллэг нэгэн зэрэг үнэн үед үнэн, ядаж нэг нь
худал байхад худал байдаг хэллэгийг A ба B
хэллэгийн конъюнкц гээд AB гэж тэмдэглэдэг.
Ба, бөгөөд гэсэн холбоосоор холбогдоно.
 A ба B хэллэгүүдийн ядаж нэг нь үнэн байхад
үнэн, хоѐулаа нэгэн зэрэг худал үед худал байдаг
хэллэгийг A ба B хэллэгийн дизъюнкц гээд AB гэж
тэмдэглэдэг. Эсвэл гэсэн холбоосоор холбогдоно


20. АНХААРАЛ ХАНДУУЛСАН
ТА БҮХЭНД БАЯРЛАЛАА