Introduction to Crystal Plasticity Modelling

Introduction to Crystal Plasticity Modelling

• 1.
  Crystal Plasticity FiniteElement Modelling Crystal Plasticity Finite Element Modelling CDT Lecture – Nov 2018 Suchandrima Das suchandrima90@gmail.com
• 2.
  Crystal Plasticity FiniteElement Modelling Recap of important concepts
• 3.
  Crystal Plasticity FiniteElement Modelling Crystalline solids: Quick Recap Crystal: Highly regular arrangement of atoms • how do we describe them ? - lattices • how can we study their structures ? many ways, for example x-ray diffraction. 1-D Lattice Crystal structures repeat in 3D Motif  Single atom OR groups of atoms (unit cell) Space Lattice + Motif = Crystal Structure https://www.seas.upenn.edu/~chem101/sschem/solidstatechem.html/
• 4.
  Crystal Plasticity FiniteElement Modelling Crystalline solids: Quick Recap 7 Crystal Systems: 7 unique unit-cell shapes 14 Bravais Lattices https://www.seas.upenn.edu/~chem101/sschem/solidstatechem.html/
• 5.
  Crystal Plasticity FiniteElement Modelling Plasticity Linear elastic – return to original shape upon removal of load Plastic  Beyond yield point Permanent deformation Energy dissipated Path dependent Due to dislocation generation and movement
• 6.
  Crystal Plasticity FiniteElement Modelling How does plastic deformation occur? Not a rigid body slip phenomenon Part slipped Part not yet slipped Dislocation Line: Line defect
• 7.
  Crystal Plasticity FiniteElement Modelling 1 plane of atoms slides over adjacent plane by defect motion (dislocations). Adapted from Fig. 7.1, Callister 7e. Note: Process is isochoric Dislocations: Key Points
• 8.
  Crystal Plasticity FiniteElement Modelling Plastic deformation G. Dieter, Mechanical Metallurgy, 3rd Edition, McGraw-Hill, 1986. Energy barrier ΔE minimized  growing slipped area by advancing DISLOCATION Dislocations: Key Points Caterpillar hump  extra half plane of atoms Subsequent bond breaking and bond forming Note: Process is isochoric
• 9.
  Crystal Plasticity FiniteElement Modelling Dislocation Recap Material displaces by ‘b’ Key points to remember: • Dislocations are line defects • Plastic deformation occurs by dislocation glide • No volume change involved
• 10.
  Crystal Plasticity FiniteElement Modelling ** https://www.mm.ethz.ch/teaching.html ** Micro Meso Macro Bulk  Many single crystals + GB Multiscale Modelling CPFE lies in meso-scale region
• 11.
  Crystal Plasticity FiniteElement Modelling Polycrystalline Grain Structure CPFE needs information about the orientation of the crystal Electron Backscatter Diffraction Orientation  Sample relative to the crystal Electrons diffracted from samples create diffraction patterns. Positions of bands  orientation
• 12.
  Crystal Plasticity FiniteElement Modelling Crystallographic Orientation: EBSD Intro Important to acquire information about the orientation of each grain in the polycrystal Electron Backscatter Diffraction Electrons leaving sample Some exit at Bragg condition Bragg condition  spacing of lattice planes Electrons diffract  Kikuchi bands Bands  phase & orientation
• 13.
  Crystal Plasticity FiniteElement Modelling Crystallographic Orientation: EBSD Intro EBSD gives us the Euler angles Euler Angles  3 angles through which the crystal must be rotated in order to relate the crystallographic axes with the sheet reference axes 1 2 3 4
• 14.
  Crystal Plasticity FiniteElement Modelling Why do we need CPFE?
• 15.
  Crystal Plasticity FiniteElement Modelling Crystal plasticity Crystalline materials Thermal & Mechanical Behavior Microstructure Critical Role played by:  Texture & orientation of Single crystals  Total area of GBs EXAMPLE  Hall-Petch relationship  Smaller the grain  Stronger the polycrystal. Why?  Effect cannot be captured by macroscopic continuum model.
• 16.
  Crystal Plasticity FiniteElement Modelling Hall-Petch effect & Dislocations: Key Points So how does Hall-Petch effect come by? GB offer resistance to dislocation motion. Why? https://en.wikipedia.org/wiki/Grain_bo undary_strengthening#/ pileup_force> GB_Repulsive force ; deformation continues Pile-up increases, pileup_force increases. Dislocations pile-up. Orientation mismatch : hinders dislocation motion. GB_Repulsive force GB – boundary between 2 grains of diff orientation Smaller grain Lesser pile-up More difficult to move dislocation across GB Stronger material
• 17.
  Crystal Plasticity FiniteElement Modelling Polycrystal plasticity Single crystal plasticity Homogenization Polycrystal plasticity Assumption: GB do not play an active role in plastic deformation other than providing a constraint on plastic strain of neighboring grains (G.I.Taylor 1938). Assumption confirmed by exp at ambient temp. At high temp. GB sliding & diffusion  creep Each single crystal  elastically & plastically anisotropic Aggregation of many grains  Isotropic Assumption: lengthscale ‘l’ over which fields of interest (e.g. strain) varies is << than macroscopic lengthscale ‘L’. ‘Effective homogeneous material’  relaxed continuity requirements
• 18.
  Crystal Plasticity FiniteElement Modelling Crystallographic Slip: Theory
• 19.
  Crystal Plasticity FiniteElement Modelling Single Crystal Slip systems Stretching single crystal  Slip on crystallographic planes along specific directionsStretching single crystal  Slip on crystallographic planes along specific directions Remember: There is an energy barrier to dislocation slip. Inherent resistance to deformation by crystal lattice Peierls stress is the shear stress required to move a dislocation through a crystal lattice at 0 K. Peierls found 𝜏 = 𝐺exp − 2𝜋𝑤 𝑏 Large w and small b will reduce 𝜏
• 20.
  Crystal Plasticity FiniteElement Modelling Single Crystal Slip systems Width  measure of degree of disruption a dislocation creates wrt perfect lattice 𝜏 = 𝐺exp − 2𝜋𝑤 𝑏 Large w and small b will reduce 𝜏 Therefore, slip most likely to occur in close-packed planes in close-packed directions.
• 21.
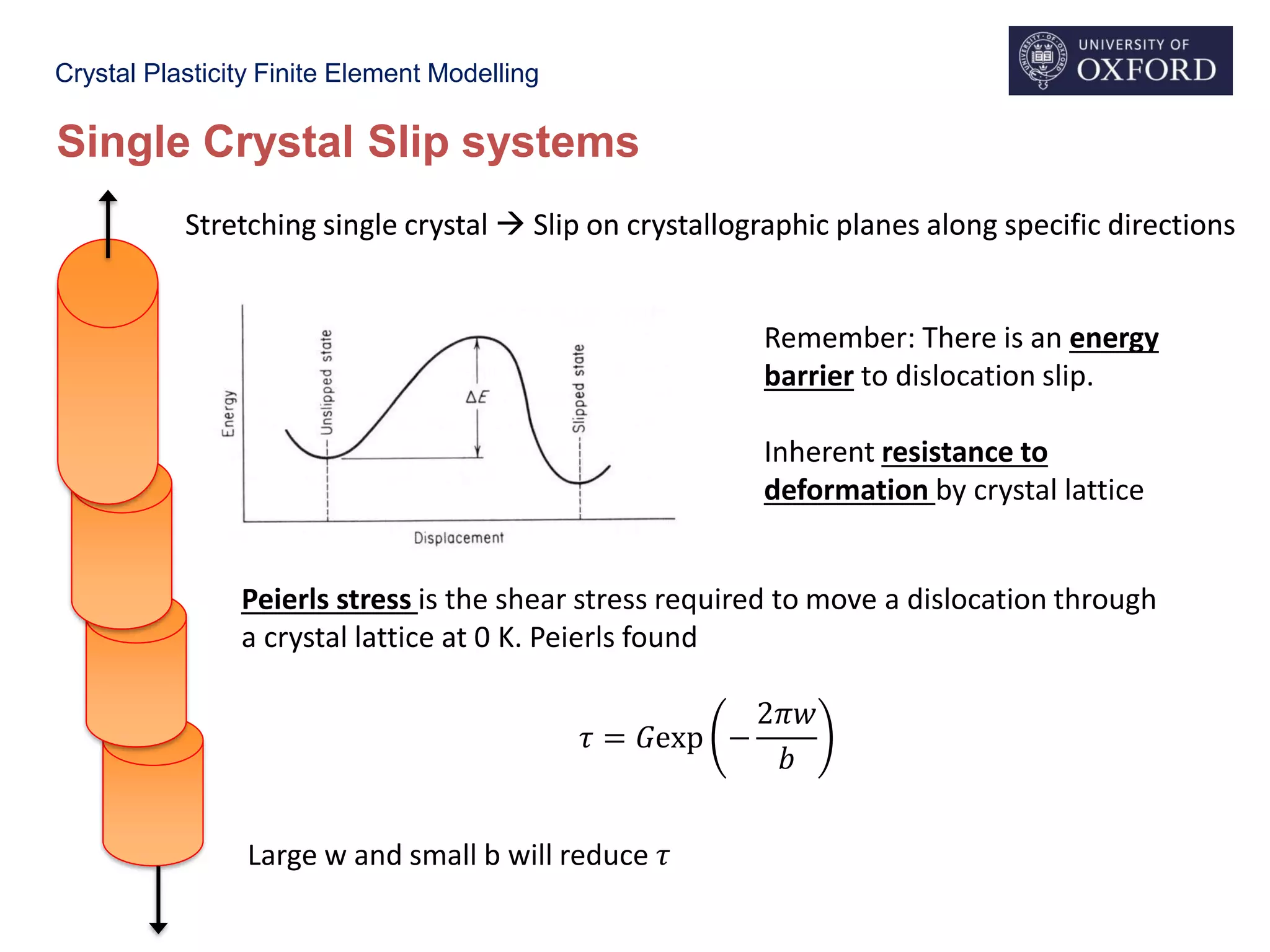
  Crystal Plasticity FiniteElement Modelling Single Crystal Slip systems Stretching single crystal  Slip on crystallographic planes along specific directions Slip Directions: Shortest Lattice repeat vectors Slip Planes: Planes with highest in-plane density Stretching single crystal  Slip on crystallographic planes along specific directions X Y Z (111) ½[𝟏ഥ𝟏 𝟎] FCC Z X Y (110) ½[ഥ𝟏𝟏𝟏] BCC Q. How many slip systems in BCC & FCC?
• 22.
  Crystal Plasticity FiniteElement Modelling Schmid Factor https://www.doitpoms.ac.uk/tlplib/slip/slip_geometry.php Angle between Ԧ𝒍 and 𝑺 = λ Angle between Ԧ𝒍 and 𝒏 = Φ cos λ = Ԧ𝒍. 𝑺 cos Φ = Ԧ𝒍. 𝒏 τ  Shear stress on plane 𝒏 along 𝑺 γ  Shear strain on plane 𝒏 along 𝑺 𝜏 = 𝑷. 𝑚 𝒎 = 𝒄𝒐𝒔 𝝀 𝒄𝒐𝒔 𝜱 = Schmid Factor How much normal stress can be effectively transferred on to the slip plane as shear stress?
• 23.
  Crystal Plasticity FiniteElement Modelling Slip occurs when the shear stress acting in the slip direction on the slip plane reaches some critical value  CRSS https://www.doitpoms.ac.uk/tlplib/slip/slip_geometry.php Critically Resolved Shear Stress 𝜏 𝐶 = 𝝈 𝑦. 𝑚 𝝈 𝑦 = 𝜏 𝐶 𝑚 𝑚  Depends on relative orientation of loading axis w.r.t slip systems Hence, we expect 𝝈 𝑦 of single crystal to be orientation- dependent (but not on tension vs. compression) FCC obeys this law well BCC shows tension compression asymmetry 𝝉 𝑹 > 𝝉 𝑪 For deformation Yield stress and Schmid Factor
• 24.
  Crystal Plasticity FiniteElement Modelling Taylor Factor: Quick Look Further Info: https://nptel.ac.in/courses/113108054/module4/lecture17.pdf https://inis.iaea.org/collection/NCLCollectionStore/_Public/29/000/29000976.pdf 𝝈 𝑦 = 𝜏 𝐶 𝑚 Macroscopic yield stress  Schmid factor of single grain Different yield stress for applied stress along different directions Active slip system  one with smallest m Single Crystals • Crystal cannot change its shape freely  Constraints from surrounding crystals • Grains must fit together without voids after deformation • Several slip systems should be activated in a grain, or in a part of grain • Slip from 5 independent slip systems is generally required to accommodate the five independent strain components for plastic deformation (Taylor 1938) • Active combination  combination of 5 systems which minimizes accumulated slip • Uniaxial tension in X direction 𝑀 = σ 𝑖 ሶ𝛾 𝑖 ሶ𝜀11 𝑃 ; 𝝈 𝑦 = 𝜏 𝐶 𝑀 • Assumption: Strain and strain rate in any grain = Average strain Poly Crystals
• 25.
  Crystal Plasticity FiniteElement Modelling Plasticity So we know now that dislocations gliding bring about plastic deformation. Then how do they cause hardening? Due to dislocation generation and movement
• 26.
  Crystal Plasticity FiniteElement Modelling Dislocation Hardening material hardens slip rate reduced more obstacles created Dislocation density increases progressive plastic deformation Dislocations multiply and entangle with one another Distance of separation between them reduces. They restrict each others motion. Dislocation motion becomes more difficult
• 27.
  Crystal Plasticity FiniteElement Modelling Dislocation Hardening Dislocations SSD Inherently present. No material is perfect GND To accommodate strain gradient
• 28.
  Crystal Plasticity FiniteElement Modelling SSDs & GNDs Extra half plane of atoms. So there is lattice distortion around the dislocation; Bonds are bent or strained. Dislocations  Generate strain field around them No effective strain field  SSDs Effective strain field  GNDs If you zoom in and just see one dislocation, is it a SSD or GND?
• 29.
  Crystal Plasticity FiniteElement Modelling Direction of dislocation slip Non-uniform shear applied
• 30.
  Crystal Plasticity FiniteElement Modelling What do we know so far? • Plastic deformation  Permanent deformation & path dependent • Dislocations are line defects • Plastic deformation occurs by dislocation glide • Dislocations glide on slip systems when the 𝝉 𝑹 > 𝝉 𝑪 • Dislocations bring about hardening. Jiang J, Zhang T, Dunne FPE, Britton TB. 2016 Deformation compatibility in a single crystalline Ni superalloy. Proc.R.Soc.A 472: 20150690
• 31.
  Crystal Plasticity FiniteElement Modelling What do we want to know from CPFE? Remember  Continuum macroscopic model does not consider dislocation slip. Primarily we want CPFE to consider this. Given • Slip systems; Crystal • Elastic properties • Orientation • Apply macroscopic loading CPFE • Resolve load into assigned slip systems • Calculate slip if there is any • Resulting plastic strain • Lattice rotation • Dislocation density UMAT
• 32.
  Crystal Plasticity FiniteElement Modelling Remember: Schmid Factor https://www.doitpoms.ac.uk/tlplib/slip/slip_geometry.php Angle between Ԧ𝒍 and 𝑺 = λ Angle between Ԧ𝒍 and 𝒏 = Φ cos λ = Ԧ𝒍. 𝑺 cos Φ = Ԧ𝒍. 𝒏 τ  Shear stress on plane 𝒏 along 𝑺 γ  Shear strain on plane 𝒏 along 𝑺 𝜏 = 𝑷. 𝑚 𝒎 = 𝒄𝒐𝒔 𝝀 𝒄𝒐𝒔 𝜱 = Schmid Factor How much normal stress can be effectively transferred on to the slip plane as shear stress?
• 33.
  Crystal Plasticity FiniteElement Modelling What do we want to know from CPFE? Remember  Continuum macroscopic model does not consider dislocation slip. Primarily we want CPFE to consider this. Given • Slip systems; Crystal • Elastic properties • Orientation • Apply macroscopic loading CPFE • Resolve load into assigned slip systems • Calculate slip if there is any • Resulting plastic strain • Lattice rotation • Dislocation density UMAT
• 34.
  Crystal Plasticity FiniteElement Modelling Slip occurs when the shear stress acting in the slip direction on the slip plane reaches some critical value  CRSS Critically Resolved Shear Stress 𝝉 𝑹 > 𝝉 𝑪 For deformation
• 35.
  Crystal Plasticity FiniteElement Modelling Crystallographic Slip 𝜷 𝒑 Crystallographic slip rate ሶ𝛽 𝑝 𝜆 Crystallographic slip ሶ𝛽 𝑝 𝜆 ∆𝑡 = ∆𝛽 𝑝 𝜆 Summed over all slip systems ෍ λ=1 𝑛 ሶ𝛽 𝑝 𝜆 ∆𝑡 = ∆𝛽 𝑝 Summed over time 𝛽 𝑝 𝑡+∆𝑡 = 𝛽 𝑝 𝑡 + ෍ λ=1 𝑛 ሶ𝛽 𝑝 𝜆 ∆𝑡 In FE We progress from time 𝑡 to 𝑡 + ∆𝑡 For each time increment ∆𝑡, it is useful to develop the formulation in terms of rate. Some formulations like viscoplasticity are rate dependent. Plasticity is an incremental process. Instead of dealing with increments in slip, we consider slip rate. Rate of slip is calculated So we need to find ሶ𝜷 𝒑 𝝀 to find 𝛽 𝑝
• 36.
  Crystal Plasticity FiniteElement Modelling Finding ሶ𝜷 𝑝 Constitutive Slip Law is used to define how much slip will take place ሶ𝛽 𝑝 𝜆 ∝ 𝑓 𝜏, 𝜏 𝐶 Can be a simple power law 1. Phenomenological: Commonly Used Power Law ሶ𝛽 𝑝 𝜆 = K 𝜏 𝜏 𝐶 𝑛 for 𝜏 > 𝜏 𝐶
• 37.
  Crystal Plasticity FiniteElement Modelling Finding ሶ𝜷 𝑝 2. Physically Based Slip Law Thermally activated process of movement of dislocations, overcoming pinning obstacles ሶ𝛽 𝑝 𝜆 = 𝑞 𝑣 𝜆 𝑏 𝜆 𝐿ℎ = 𝜌 𝑚 𝜆 𝑏 𝜆 𝑣 𝜆 𝑣 = 𝑑𝛤 = 𝑑 𝜈𝑏 𝜆 2𝑙 exp − ∆𝐺 𝑘𝑇 ∆𝐺 = ∆𝐹 − 𝜏𝑉 ሶ𝛽 𝑝 𝜆 = 𝜌 𝑔 𝜈 𝑏 𝜆 2 exp − ∆𝐹 𝜆 𝑘𝑇 sinh sgn(𝜏 𝜆)( 𝜏 𝜆 − 𝜏 𝑐 𝜆)𝑉 𝜆 𝑘𝑇 ሶ𝛽 𝑝 𝜆 = α sinh(β( 𝜏 𝜆 − 𝜏 𝑐 𝜆 ))
• 38.
  Crystal Plasticity FiniteElement Modelling What do we want to know from CPFE? Remember  Continuum macroscopic model does not consider dislocation slip. Primarily we want CPFE to consider this. Given • Slip systems; Crystal • Elastic properties • Orientation • Apply macroscopic loading CPFE • Resolve load into assigned slip systems • Calculate slip if there is any • Resulting plastic strain • Lattice rotation • Dislocation density UMAT
• 39.
  Crystal Plasticity FiniteElement Modelling How to find strain, rotation and dislo density? ሶ𝜷 𝑝 or 𝜷 𝒑 F L Strain Rotation Total lattice deformation  Gradient GND
• 40.
  Crystal Plasticity FiniteElement Modelling Deformation Gradient U determines deformation: • Translation • Rigid Body rotation • Stretch/Shape change • Or a combination Second-order tensor Maps the undeformed state to the deformed state of a sample 𝑭 = 𝜕𝒙 𝜕𝑿 = 𝑰 + 𝜕𝒖 𝜕𝑿 = 𝑰 + 𝜷 Representation Analogous to strain for small deformations Displacement gradient Infinitesimal line element dX becomes dx 𝑭 Contains all the information about stretch, rotation, translation.
• 41.
  Crystal Plasticity FiniteElement Modelling F.P.E.Dunne: Lecture – The Crystal Approach 2014 Examples of Deformation
• 42.
  Crystal Plasticity FiniteElement Modelling Deformation Gradient Calculation 𝜕𝒙 = 𝑭 𝜕𝑿 𝑑𝒙 𝑑𝒚 𝑑𝒛 = 𝑭 𝑥𝑋 𝑭 𝑥𝑌 𝑭 𝑥𝑍 𝑭 𝑦𝑋 𝑭 𝑦𝑌 𝑭 𝑦𝑍 𝑭 𝑧𝑋 𝑭 𝑧𝑌 𝑭 𝑧𝑍 𝑑𝑿 𝑑𝒀 𝑑𝒁 = 𝜕𝒙 𝜕𝑿 𝜕𝒙 𝜕𝒀 𝜕𝒙 𝜕𝒁 𝜕𝒚 𝜕𝑿 𝜕𝒚 𝜕𝒀 𝜕𝒚 𝜕𝒁 𝜕𝒛 𝜕𝑿 𝜕𝒛 𝜕𝒀 𝜕𝒛 𝜕𝒁 𝑑𝑿 𝑑𝒀 𝑑𝒁 𝑭
• 43.
  Crystal Plasticity FiniteElement Modelling Deformation Gradient Calculation: Examples F.P.E.Dunne: Lecture – The Crystal Approach 2014
• 44.
  Crystal Plasticity FiniteElement Modelling Deformation Gradient Calculation: Examples F.P.E.Dunne: Lecture – The Crystal Approach 2014 𝑭 Contains all the information about stretch, rotation, translation. How can we extract strain and rotation from it?
• 45.
  Crystal Plasticity FiniteElement Modelling How to find strain, rotation and dislo density? ሶ𝜷 𝑝 or 𝜷 𝒑 F L Strain Rotation Total lattice deformation  Gradient GND So we know what is 𝑭 Is this only computed for CPFE? Any FE implementation undergoing plastic deformation will compute 𝑭 So what does CPFE do in this context?
• 46.
  Crystal Plasticity FiniteElement Modelling Splitting F Introduce an intermediate imaginary configuration dp 𝑑𝒑 = 𝑭 𝑝 𝑑𝑿 𝑑𝒙 = 𝑭 𝑒 𝑑𝒑 𝑑𝒑 = 𝑭 𝑝 𝑑𝑿 = 𝑭 𝑒−1 𝑑𝒙 𝑭 = 𝝏𝒙 𝝏𝑿 = 𝑭 𝒆 𝑭 𝒑 𝑭 can be split into the elastic (𝑭 𝑒 ) and the plastic (𝑭 𝑝 ) component CPFE considers plastic deformation by dislocation slip and computes the resulting 𝑭 𝒑
• 47.
  Crystal Plasticity FiniteElement Modelling Plastic Deformation Gradient How can we calculate 𝑭 𝒑 ? 𝑭 𝑃 = ෍ 𝜆 𝛽 𝑝 𝜆 𝒔 𝜆 ⨂𝒎 𝜆 crystallographic slip 𝜷 𝑝 s  Slip direction M  Slip normal 𝜆  A particular Slip system Just like we consider slip rate, we will also consider the rate of 𝑭 𝑃 i.e. ሶ𝑭 𝑝 ሶ𝑭 𝑝 = ෍ 𝜆 ሶ𝛽 𝑝 𝜆 𝒔 𝜆⨂𝒎 𝜆 Remember  Any FE implementation undergoing plastic deformation will compute 𝑭 CPFE will compute 𝑭 𝑷 & ሶ𝑭 𝒑 by considering dislocation slip. Knowing 𝑭 and 𝑭 𝑷 , you can then compute 𝑭 𝒆
• 48.
  Crystal Plasticity FiniteElement Modelling How to find strain, rotation and dislo density? ሶ𝜷 𝑝 or 𝜷 𝒑 F L Strain Rotation Total lattice deformation  Gradient GND So we know what is 𝑭 and how we can compute its elastic and plastic components. Now what is L? We have discussed so far rate quantities like ሶ𝜷 𝑝 & ሶ𝑭 𝑝. L is a form used to represent ሶ𝑭 𝑝 . Simply, 𝑳 = 𝜕𝒗 𝜕𝒙 = ሶ𝑭𝑭−1 (theoretically  spatial rate of change of velocity). FE implementation will compute L. Once again we need CPFE to compute its plastic component. So how to get strain and rotation from L?
• 49.
  Crystal Plasticity FiniteElement Modelling Velocity Gradient L Symmetric Component 1 2 𝑳 + 𝑳 𝑇 rate of deformation D Stretch related Anti-Symmetric Component 1 2 𝑳 − 𝑳 𝑇 continuum spin W Rotation related 𝑳 𝑒 𝑳 𝑝 1 2 𝑳 𝑝 + 𝑳 𝑝 𝑇 1 2 𝑳 𝑝 − 𝑳 𝑝 𝑇 𝑫 𝑝 = 𝑾 𝑝 = 1 2 𝑳 𝑒 + 𝑳 𝑒 𝑇 1 2 𝑳 𝑒 − 𝑳 𝑒 𝑇 𝑫 𝑒 = 𝑾 𝑒 =
• 50.
  Crystal Plasticity FiniteElement Modelling Equations to complete the picture We know the slip rate from the slip law
• 51.
  Crystal Plasticity FiniteElement Modelling Finding ሶ𝜷 𝑝 Constitutive Slip Law is used to define how much slip will take place ሶ𝛽 𝑝 𝜆 ∝ 𝑓 𝜏, 𝜏 𝐶 Can be a simple power law 1. Phenomenological: Commonly Used Power Law ሶ𝛽 𝑝 𝜆 = K 𝜏 𝜏 𝐶 𝑛 for 𝜏 > 𝜏 𝐶
• 52.
  Crystal Plasticity FiniteElement Modelling Crystallographic Slip 𝜷 𝒑 Crystallographic slip rate ሶ𝛽 𝑝 𝜆 Crystallographic slip ሶ𝛽 𝑝 𝜆 ∆𝑡 = ∆𝛽 𝑝 𝜆 Summed over all slip systems ෍ λ=1 𝑛 ሶ𝛽 𝑝 𝜆 ∆𝑡 = 𝛽 𝑝 Summed over time 𝛽 𝑝 𝑡+∆𝑡 = 𝛽 𝑝 𝑡 + ෍ λ=1 𝑛 ሶ𝛽 𝑝 𝜆 ∆𝑡 In FE We progress from time 𝑡 to 𝑡 + ∆𝑡 For each time increment ∆𝑡, it is useful to develop the formulation in terms of rate. Some formulations like viscoplasticity are rate dependent. Plasticity is an incremental process. Instead of dealing with increments in slip, we consider slip rate. Rate of slip is calculated So we need to find ሶ𝜷 𝒑 𝝀 to find 𝛽 𝑝
• 53.
  Crystal Plasticity FiniteElement Modelling How to find strain, rotation and dislo density? ሶ𝜷 𝑝 or 𝜷 𝒑 F L Strain Rotation Total lattice deformation  Gradient GND
• 54.
  Crystal Plasticity FiniteElement Modelling Equations to complete the picture 𝑳 𝑝 ≅ ሶ𝑭 𝑝 𝑳 𝑒 = 𝑳-𝑭 𝑒 𝑳 𝑝 𝑭 𝑒−1 𝑭 𝑃 = ෍ 𝜆 𝛽 𝑝 𝜆 𝒔 𝜆 ⨂𝒎 𝜆 ሶ𝑭 𝑝 = ෍ 𝜆 ሶ𝛽 𝑝 𝜆 𝒔 𝜆 ⨂𝒎 𝜆 We will know F from FE, so we can find 𝑭 𝒆 𝑭 = 𝝏𝒙 𝝏𝑿 = 𝑭 𝒆 𝑭 𝒑 We also know L from FE. We then find 𝑳 𝑝 & 𝑳 𝑒 We then find 𝑫 𝑝 𝑾 𝑝 𝑫 𝑒 𝑾 𝑒
• 55.
  Crystal Plasticity FiniteElement Modelling Velocity Gradient L Symmetric Component 1 2 𝑳 + 𝑳 𝑇 rate of deformation D Anti-Symmetric Component 1 2 𝑳 − 𝑳 𝑇 continuum spin W 𝑳 𝑒 𝑳 𝑝 1 2 𝑳 𝑝 + 𝑳 𝑝 𝑇 1 2 𝑳 𝑝 − 𝑳 𝑝 𝑇 𝑫 𝑝 = 𝑾 𝑝 = 1 2 𝑳 𝑒 + 𝑳 𝑒 𝑇 1 2 𝑳 𝑒 − 𝑳 𝑒 𝑇 𝑫 𝑒 = 𝑾 𝑒 =
• 56.
  Crystal Plasticity FiniteElement Modelling How to find strain, rotation and dislo density? ሶ𝜷 𝑝 or 𝜷 𝒑 F L Strain Rotation Total lattice deformation  Gradient GND We know: 𝑭 𝑃 𝑭 𝑒 𝑳 𝑃 𝑳 𝑒 𝑫 𝑃 𝑫 𝑒
• 57.
  Crystal Plasticity FiniteElement Modelling Equations to complete the picture ∆𝜺 𝑝 = 𝑫 𝑝 ∆𝑡 ∆𝜺 𝑒 = 𝑫 𝑒 ∆𝑡 ∆𝝎 𝑒 = sym 𝑳 𝑒 ∆𝑡 Jiang J, Zhang T, Dunne FPE, Britton TB. 2016 Deformation compatibility in a single crystalline Ni superalloy. Proc.R.Soc.A 472: 20150690 Continuum Rotation: Bonds at the atomic level remain unchanged. No necessary change in lattice orientation.
• 58.
  Crystal Plasticity FiniteElement Modelling What do we want to know from CPFE? Remember  Continuum macroscopic model does not consider dislocation slip. Primarily we want CPFE to consider this. Given • Slip systems; Crystal • Elastic properties • Orientation • Apply macroscopic loading CPFE • Resolve load into assigned slip systems • Calculate slip if there is any • Resulting plastic strain • Lattice rotation • Dislocation density UMAT
• 59.
  Crystal Plasticity FiniteElement Modelling Dislocation Density calculation GND can be calculated from Lattice deformation. Lattice rotation Lattice strain Total lattice deformation  Gradient  GND SSD value not evolved. But can be.
• 60.
  Crystal Plasticity FiniteElement Modelling 𝝎 𝑒 +𝜺 𝑑𝑒𝑣 𝑒 Experiments CPFE Dislocation Tensor 𝛼 𝑁𝑦𝑒 GND Density 𝝆 𝜶 𝑵𝒚𝒆 ≅ (− )𝐜𝐮𝐫𝐥(𝜺 𝒅𝒆𝒗 𝒆 + 𝝎 𝒆 ) 𝑻 𝜶 𝑵𝒚𝒆 = ෍ 𝝀 𝒃 𝝀 ໆ 𝝆 𝝀 Geometrically Necessary Dislocation Density Generated to accommodated lattice curvature
• 61.
  Crystal Plasticity FiniteElement Modelling What do we want to know from CPFE? Remember  Continuum macroscopic model does not consider dislocation slip. Primarily we want CPFE to consider this. Given • Slip systems; Crystal • Elastic properties • Orientation • Apply macroscopic loading CPFE • Resolve load into assigned slip systems • Calculate slip if there is any • Resulting plastic strain • Lattice rotation • Dislocation density UMAT
• 62.
  Crystal Plasticity FiniteElement Modelling Key Points to Remember • Dislocations are line defects • Plastic deformation occurs by dislocation glide • No volume change involved • Dislocations bring about hardening too • FE is an incremental process: Deformation computed for every Δt
• 63.
  Crystal Plasticity FiniteElement Modelling FE computes total deformation Calls CPFE UMAT Compute ∆𝜺 𝑒 ∆𝜺 𝑝 & ∆𝝎 𝑒 Compute stress increment from ∆𝜺 𝑒 Elastic and plastic deformation quantities are sent back to FE. F & L Start from time = 0, deformation has occurred for Δt Consider dislocation slip, computes slip rate, 𝐹 𝑝 & 𝐿 𝑝 Next time increment begins Key Points to Remember
• 64.
  Crystal Plasticity FiniteElement Modelling Examples
• 65.
  Crystal Plasticity FiniteElement Modelling Y ZX [100] [110] [1-10] 5 µm 5 µm • Substantial Increase in Pile Up • Slip localization • Higher max load 0 30 60 90 0 200 400 600 LoadonElement(mN) Depth (nm) Load vs Depth Implanted Unimplanted Nano-Indentation  SEM [010] 4.2 µm radius; 500 nm deep Unimp He-imp S. Das et al., Scr. Mater. 146 (2018) 335–339. http://linkinghub.elsevier.com/retrieve/pii/S1359646217307145
• 66.
  Crystal Plasticity FiniteElement Modelling 𝛾ሶ 𝛼 = 𝜌 𝑔 𝜈(𝑏 𝛼 )2 exp⁡− ∆𝐹 𝛼 𝑘𝑇 sinh (𝜏 𝛼 − 𝜏 𝑐 𝛼 )𝛾0∆𝑉 𝛼 𝑘𝑇 Slip-systems – {110}<111> • 12 edge type • 4 screw type 𝑙 = 1 )𝛹(𝜌 𝐺𝑁𝐷 + 𝜌 𝑆𝑆𝐷 𝑉  spacing between the pinning dislocations 𝑙 . 𝑳 𝑝 = ෍ 𝜆 ሶ𝛾 𝛼 𝒔 𝛼 ໆ 𝒏 𝛼 ≅ ሶ𝑭 𝑝 Fitted to experiment Slip Law for slip system α Example of Nano-indentation in Tungsten https://www.sciencedirect.com/science/article/pii/S0749641918300068?via%3Dihub S. Das et al., Int. J. Plast. 109 (2018) 18–42.
• 67.
  Crystal Plasticity FiniteElement Modelling Surface Profile Prediction What happens without CPFE? S. Das et al., arXiv Prepr. arXiv1901.00745 (2018) http://arxiv.org/abs/1901.00745
• 68.
  Crystal Plasticity FiniteElement Modelling Surface Profile Prediction for different orientations https://ora.ox.ac.uk/objects/uuid:ea8aa247-fd6a-4b2d-a4be-04aa229da828
• 69.
  Crystal Plasticity FiniteElement Modelling Lattice rotation Das, S. et al. Int. J. Plast. https://doi.org/10.1016/j.ijplas.2018.05.001
• 70.
  Crystal Plasticity FiniteElement Modelling Lattice strain Das, S. et al. Int. J. Plast. https://doi.org/10.1016/j.ijplas.2018.05.001
• 71.
  Crystal Plasticity FiniteElement Modelling Thank You
• 72.
  Crystal Plasticity FiniteElement Modelling Back-up
• 73.
  Crystal Plasticity FiniteElement Modelling Strain and Rotation from F 𝑭 = 𝜕𝒙 𝜕𝑿 = 𝜕(𝑿 + 𝒖) 𝜕𝑿 = 𝑰 + 𝜕𝒖 𝜕𝑿 = 𝑰 + 𝜷 𝑰 = 𝟏 𝟎 𝟎 𝟎 𝟏 𝟎 𝟎 𝟎 𝟏 𝜷 Symmetric 1 2 𝜷 + 𝜷 𝑇 Strain Asymmetric 1 2 𝜷 − 𝜷 𝑇 Rotation For small deformations only But we want elastic and plastic components of strain. So to get that we decompose F into elastic and plastic parts.
• 74.
  Crystal Plasticity FiniteElement Modelling Dislocation Hardening ሶ𝛽 𝑝 𝜆 = 𝜌 𝑔 𝜈 𝑏 𝜆 2 exp − ∆𝐹 𝜆 𝑘𝑇 sinh sgn(𝜏 𝜆 )( 𝜏 𝜆 − 𝜏 𝑐 𝜆 )𝑉 𝜆 𝑘𝑇 𝑉 depends on the spacing between the pinning dislocations 𝑙 . Decrease mean free path of slip 𝑙 𝑙 = 1 𝛹(𝜌 𝐺𝑁𝐷 + 𝜌 𝑆𝑆𝐷) GNDs can also be introduced in the form of increasing CRSS ሶ𝛽 𝑝 𝜆 = K 𝜏 𝜏 𝐶 𝑛 for 𝜏 > 𝜏 𝐶 𝜏 𝐶 𝑡+∆𝑡 = 𝜏 𝐶 𝑡 + 𝐺𝑏 𝛹(𝜌 𝐺𝑁𝐷 + 𝜌 𝑆𝑆𝐷) 1. Phenomenological: Commonly Used Power Law 2. Physically Based Slip Law