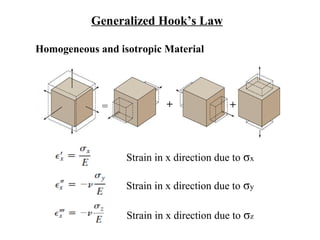
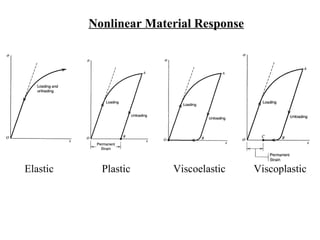
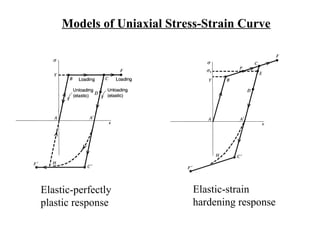
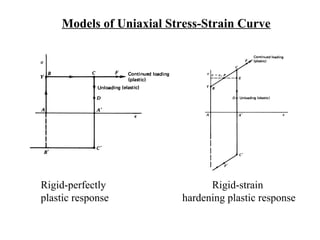
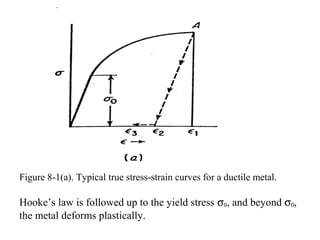
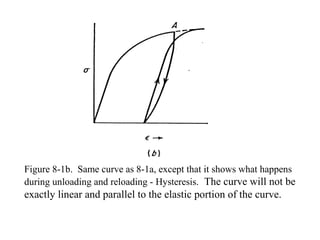
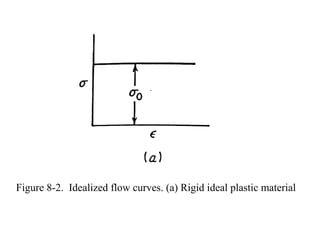
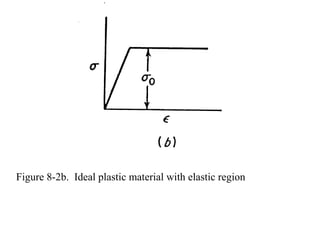
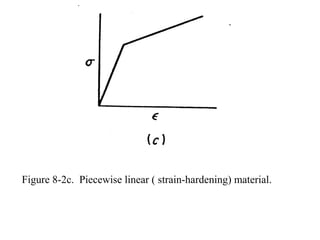
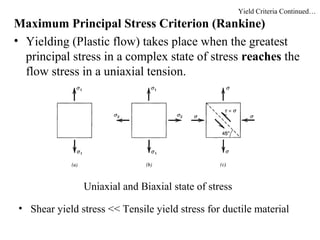
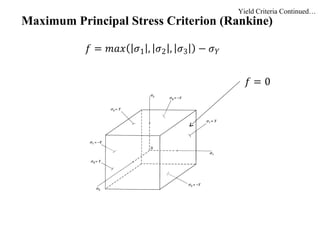
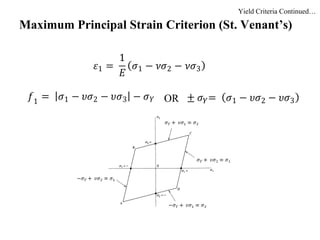
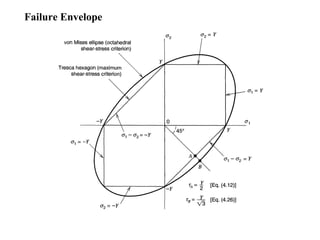
The document discusses plasticity theory and yield criteria. It introduces Hooke's law and its limitations under large strains. Generalized Hooke's law is presented for isotropic and anisotropic materials. Common stress-strain curves are shown including elastic-plastic and strain hardening responses. Several yield criteria are covered, including maximum principal stress, Tresca, and von Mises criteria. The von Mises criterion uses a second invariant of stress to predict yielding of ductile materials. An example compares predictions of yielding using Tresca and von Mises criteria for a given stress state in aluminum.

1. Unit 2
Theory of Plasticity

2. Generalized Hook’s Law
+ +=
Strain in x direction due to σx
Strain in x direction due to σy
Strain in x direction due to σz
Homogeneous and isotropic Material

3. Generalized Hook’s Law
Final Result for Homogeneous and isotropic material

4. Generalized Hook’s Law
Hook’s law for shear stress and shear strain

5. Relationship between E, ν and G
Self Study Topic

6. Hook’s Law for Anisotropic Material
Where, C11 to C66- Elastic Coefficients
Stiffness Matrix (C)

7. Hook’s Law for Anisotropic Material
Compliance Matrix (S)

8. Hook’s Law
 Orthotropic Material
 Transversely Isotropic Material

9. Nonlinear Material Response
Elastic Plastic Viscoelastic Viscoplastic

10. Models of Uniaxial Stress-Strain Curve
Experimental Stress-Strain curve

11. Elastic-perfectly
plastic response
Elastic-strain
hardening response
Models of Uniaxial Stress-Strain Curve

12. Rigid-perfectly
plastic response
Rigid-strain
hardening plastic response
Models of Uniaxial Stress-Strain Curve

13. Figure 8-1(a). Typical true stress-strain curves for a ductile metal.
Hooke’s law is followed up to the yield stress σ0, and beyond σ0,
the metal deforms plastically.

14. Figure 8-1b. Same curve as 8-1a, except that it shows what happens
during unloading and reloading - Hysteresis. The curve will not be
exactly linear and parallel to the elastic portion of the curve.

15. Figure 8-1c. Same curve as 8-1a, but showing Bauschinger effect.
It is found that the yield stress in tension is greater than the yield
stress in compression.

16. Figure 8-2. Idealized flow curves. (a) Rigid ideal plastic material

17. Figure 8-2b. Ideal plastic material with elastic region

18. Figure 8-2c. Piecewise linear ( strain-hardening) material.

19. • The theory of plasticity is concerned with a number of
different types of problems. It deals with the behavior
of metals at strains where Hooke’s law is no longer
valid.
• From the viewpoint of design, plasticity is concerned
with predicting the safe limits for use of a material
under combined stresses. i.e., the maximum load which
can be applied to a body without causing:
– Excessive Yielding
– Flow
– Fracture
YIELD CRITERIA
Three components of plasticity theory

20. • The terms yield criterion, failure criterion and flow
criterion have different meanings.
– Yield criterion (Yield strength) - applies to ductile
materials
– Failure criterion (Ultimate strength) - applies to both
ductile and brittle materials. However, it is mainly
used for brittle materials (fracture criterion), in which
the limit of elastic deformation coincides with failure.
– Flow criterion - applies to materials that have been
previously processed via work hardening (usually
ductile materials).
Yield Criteria Continued…

21. FAILURE CRITERIA: FLOW/YIELD and FRACTURE
• The Flow, Yield or Failure criterion must be in terms
of stress in such a way that it is valid for all states of
stress.
• A given material may fail by either yielding or fracture
depending on its properties and the state of stress.
• A number of different failure criteria are available,
some of which predict failure by yielding, and others
failure by fracture.
Yield Criteria Continued…

22. • Yield criterion can be expressed in the following
mathematical form:
( )Y
ij
f σσ ,
Yield Criteria Continued…

23. Yield Criteria Continued…

24. Maximum Principal Stress Criterion (Rankine)
• Yielding (Plastic flow) takes place when the greatest
principal stress in a complex state of stress reaches the
flow stress in a uniaxial tension.
Uniaxial and Biaxial state of stress
• Shear yield stress << Tensile yield stress for ductile material
Yield Criteria Continued…

25. Maximum Principal Stress Criterion (Rankine)
Yield Criteria Continued…

26. Maximum Principal Strain Criterion (St. Venant’s)
Yield Criteria Continued…
OR

27. Strain Energy Density Criterion
Yield Criteria Continued…
Strain Energy density in uniaxial tension test

28. Maximum-Shear-Stress or Tresca Criterion
• This yield criterion assumes that yielding occurs when
the maximum shear stress in a complex state of stress
equals the maximum shear stress at the onset of flow in
uniaxial-tension.
• From Eq,(2.21), the maximum shear stress is given by:
Where is the algebraically largest and is the
algebraically smallest principal stress.
2
31
max
σσ
τ
−
= (8.5)
1σ 3σ
Yield Criteria Continued…

29. For uniaxial tension, , and the maximum
shearing yield stress is given by:
Substituting in Eq. (8.3), we have
Therefore, the maximum-shear-stress criterion is given by:
032,01 === σσσσ
0τ
2
0
yσ
τ =
22
0
31
max
yσ
τ
σσ
τ ==
−
=
yσσσ 31 =− (8.6)
Yield Criteria Continued…

30. von Mises’ or Distortion-Energy Criterion
• This criterion is usually applied to ductile material
• von Mises’ proposed that yielding would occur when
the second invariant of the stress deviator J2 exceeds
some critical value.
where
2
2 kJ =
( ) ( ) ( )[ ]2
13
2
21
2
322
6
1
σσσσσσ −+−+−=J (8.7)

31. Mean and Deviator Stress

32. for yielding in uniaxial tension
for pure shear
J2 in terms of stress invariants

33. Failure Envelope

34. Additional Failure Criteria
• Octahedral Shear Stress Yield Criteria: This is another
yield criteria often used for ductile metals. It states that
yielding occurs when the shear stress on the octahedral
planes reaches a critical value.
• Mohr-Coulomb Failure Criterion: This is used for
brittle metals, and is a modified Tresca criterion.
• Griffith Failure Criterion: Another criterion used for
brittle metals. It simply states that failure will occur
when the tensile stress tangential to an ellipsoidal cavity
and at the cavity surface reaches a critical level σ0.

35. • McClintock-Walsh Criterion: Another criterion used for
brittle metals. It is an extension of the Griffith’s
criterion, and considers a frictional component acting on
the flaw faces that had to be overcome in order for them
to grow.

36. Example
A region on the surface of a 6061-T4 aluminum alloy
component has strain gage attached, which indicate the
following stresses:
σ11 = 70 MPa
σ22 = 120 MPa
σ12 = 60 MPa
Determine the yielding for both Tresca’s and von Mises’
criteria, given that σ0 = 150 MPa (the yield stress).

37. Solution
Since we were given the value of σ12, we must therefore
first establish the principal stresses. Invoke Eq. 4-37.
Hence,
σ1 = 160 MPa; σ2 = 30 MPa; σ1 = 0
According to Tresca, τmax = (160 - 0)/2 = 80 MPa
For yielding in uniaxial tension:
σ0/2 = 75 MPa
Since the 80 MPa > 75 MPa, Tresca criterion would be
unsafe.








+




 −
±
+
= 2
12
2
22112211
21
22
, σ
σσσσ
σσ

38. The von Mises criterion can be invoked from Eq. 8-9.
The L.H.S. of the above Eq. gives a value of 175 MPa.
This criterion predicts that the material will not fail (flow),
unlike the Tresca criterion, which predicts that the material
will flow.
Therefore, the Tresca criterion is more conservative than
the von Mises’ criterion in predicting failure.
[ ] 2/12
13
2
32
2
21 )()()(
2
1
σσσσσσσ −+−+−=o