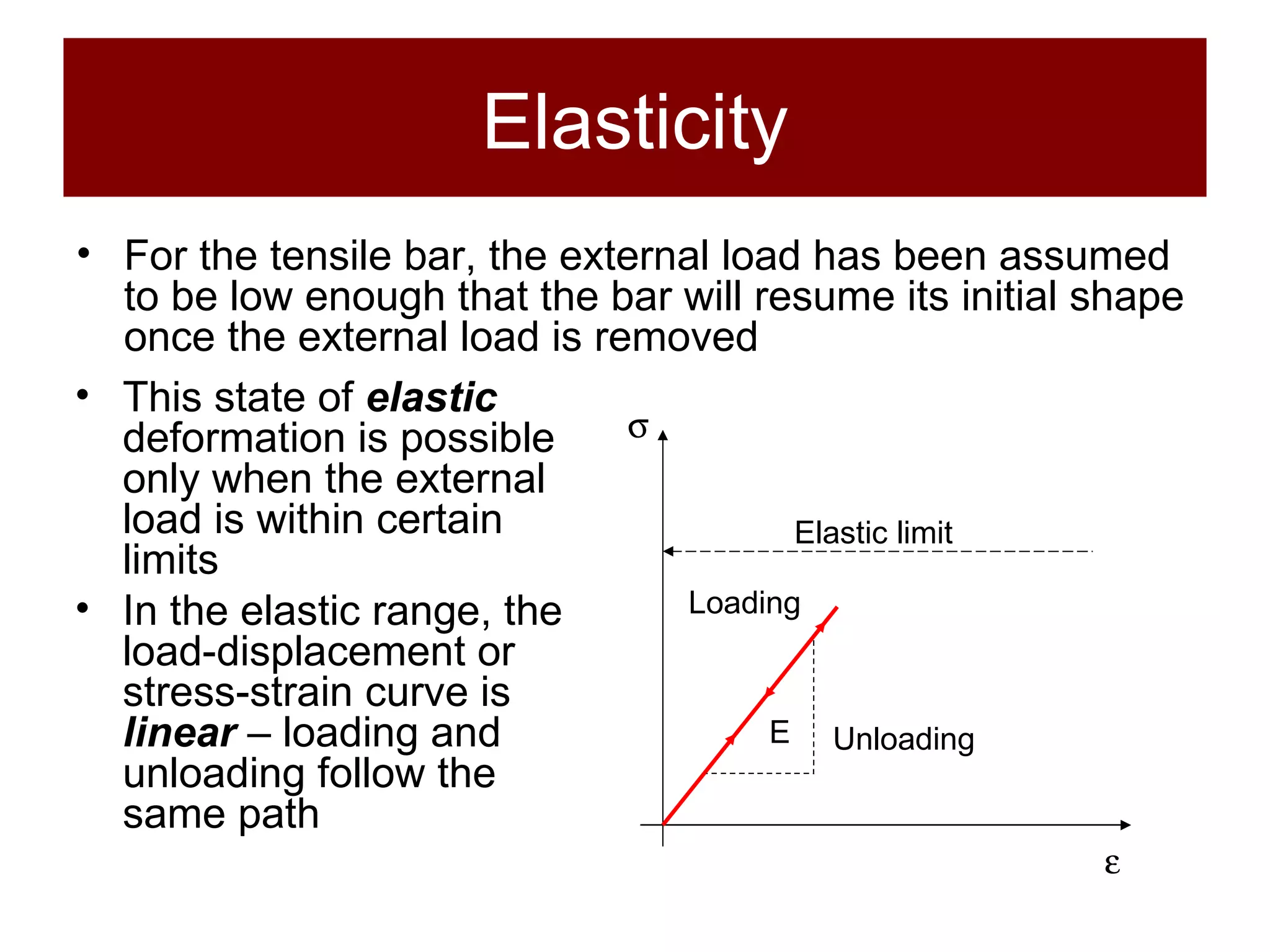
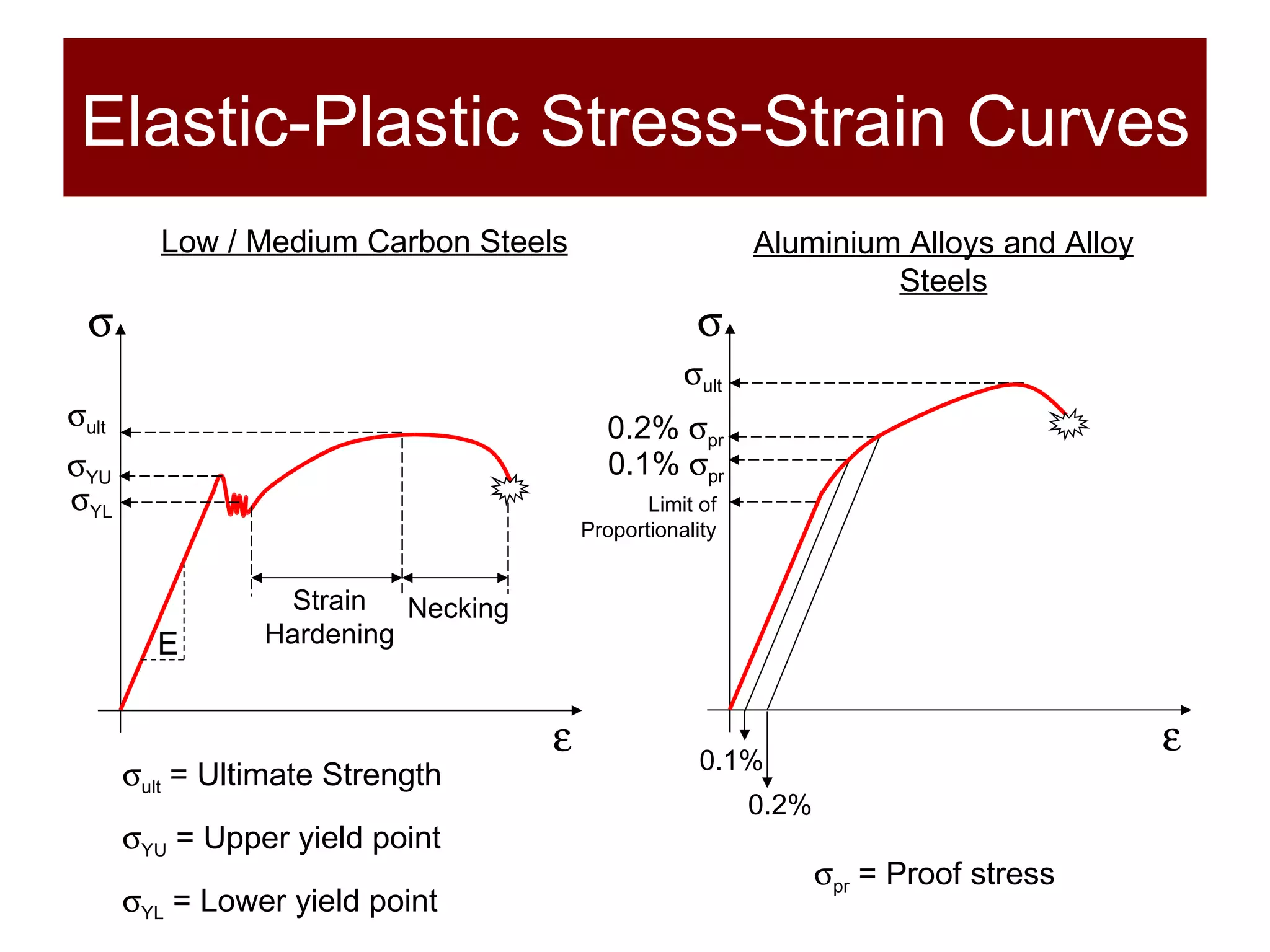
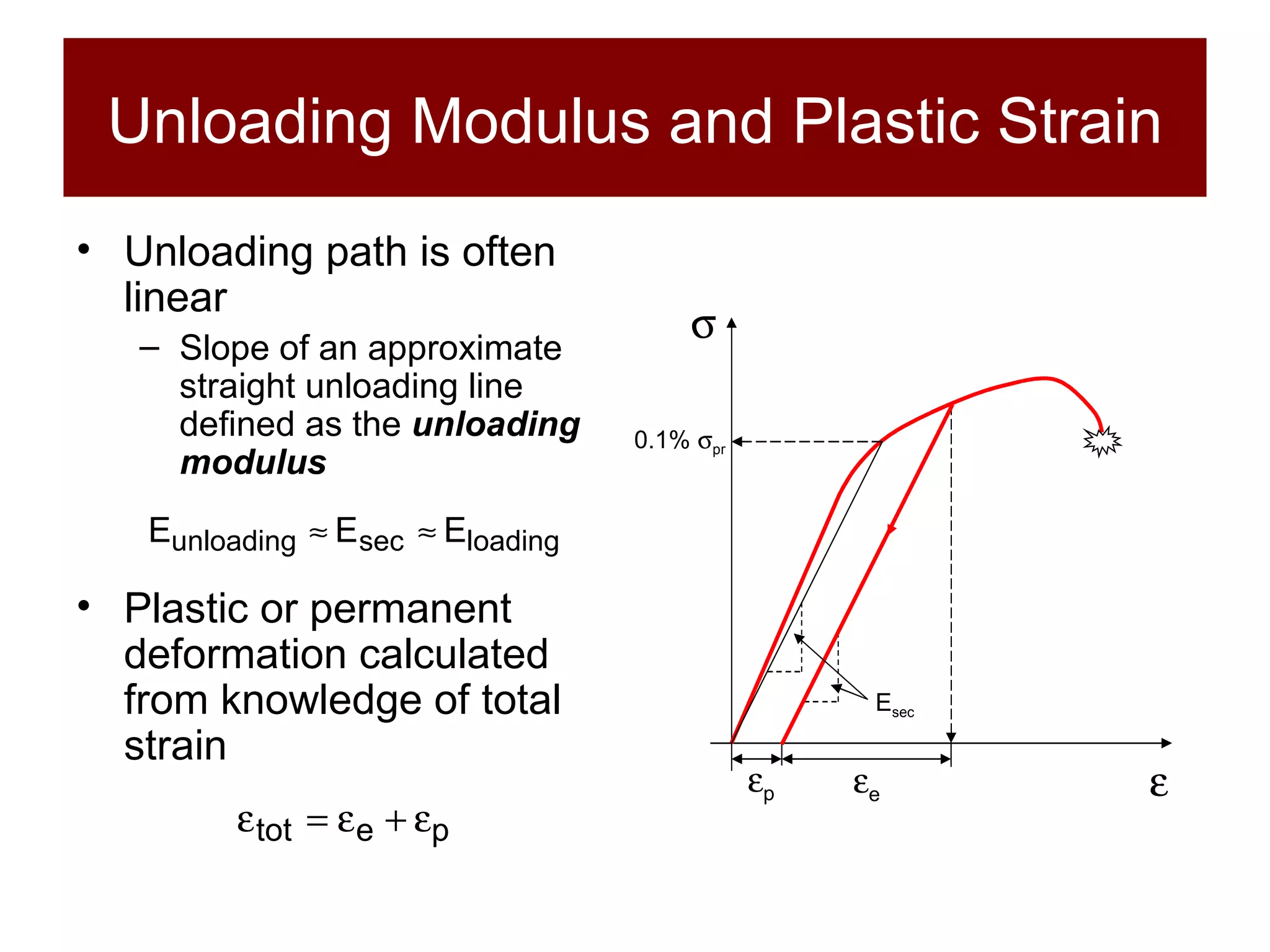
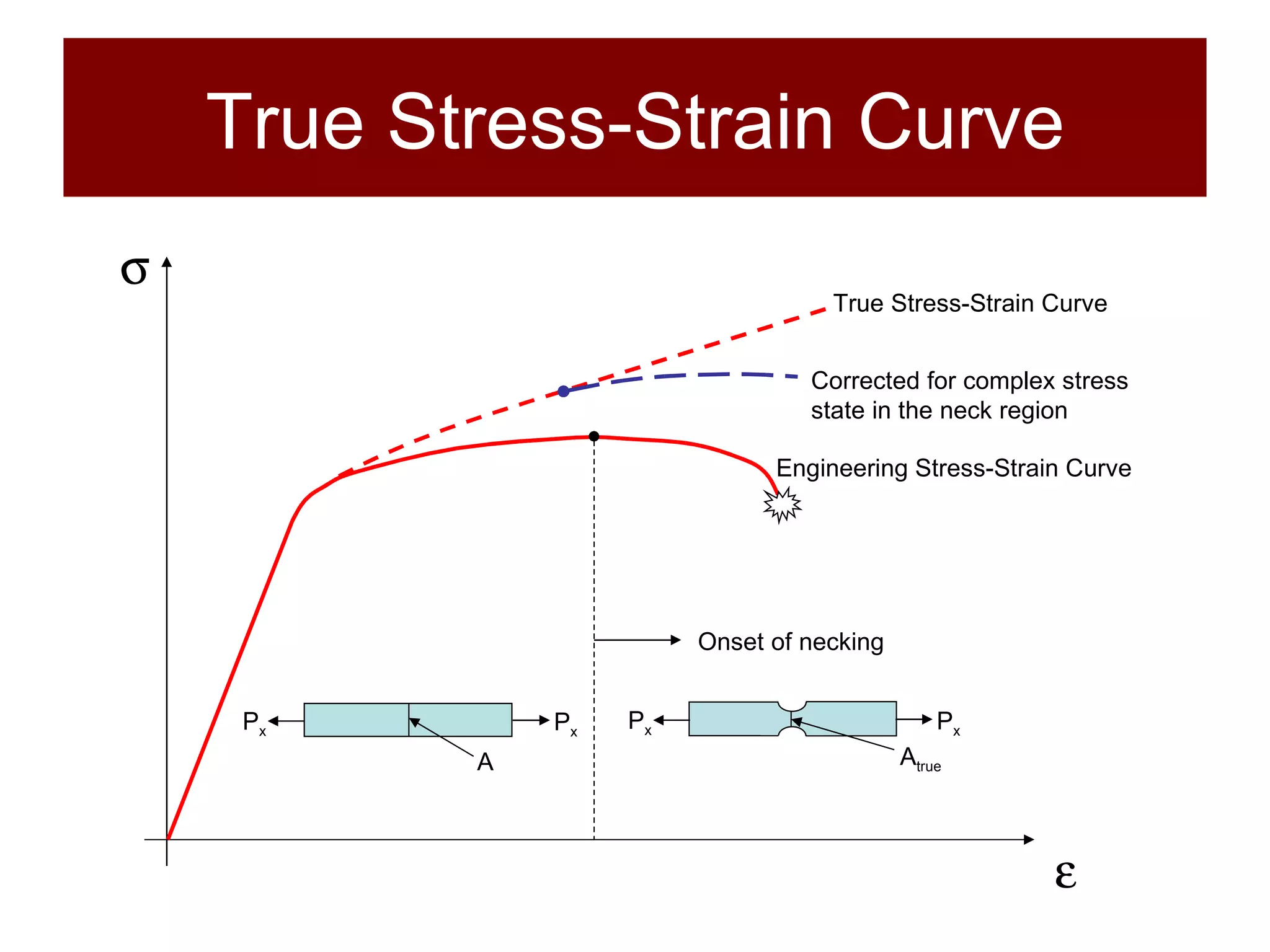
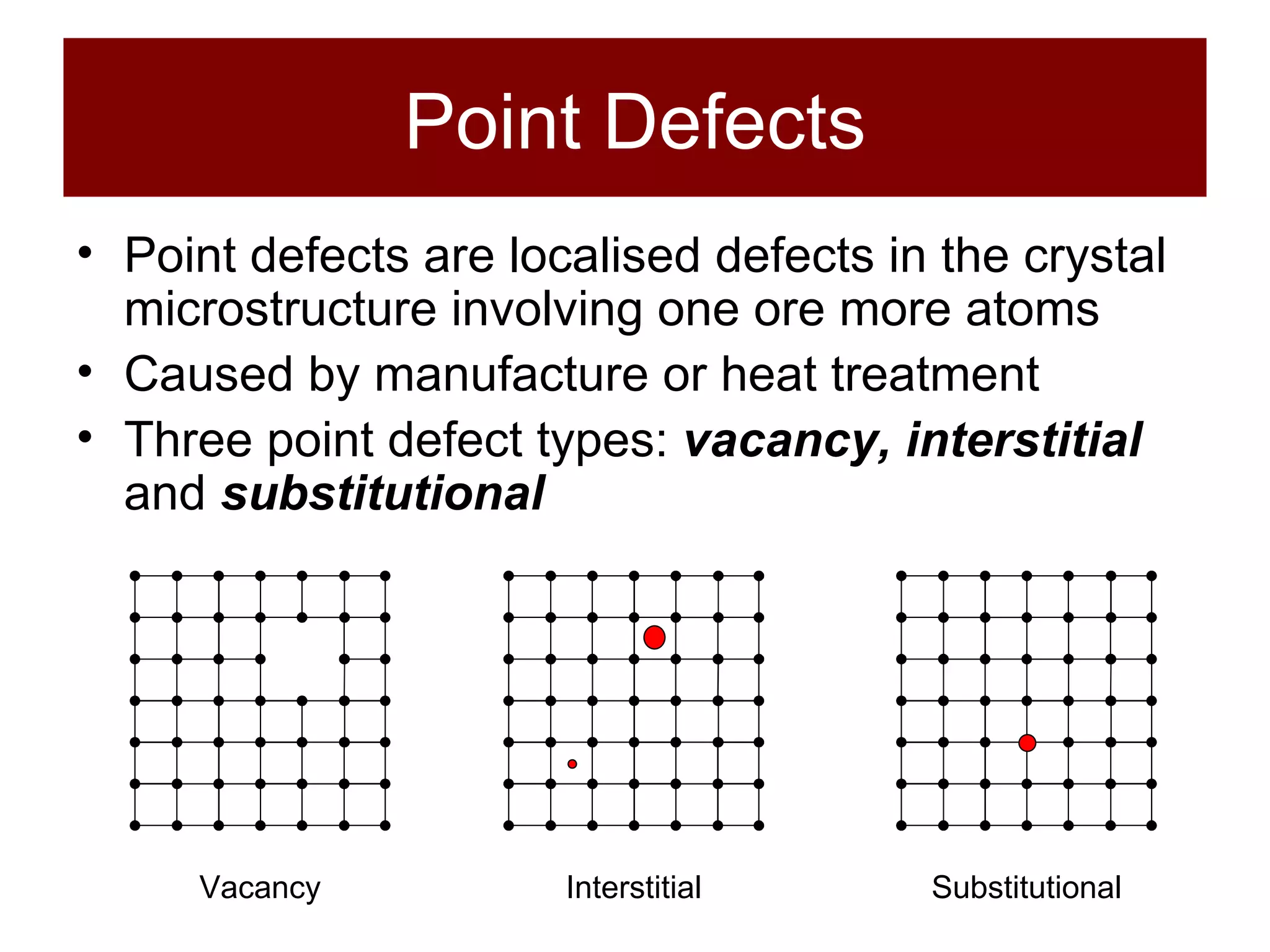
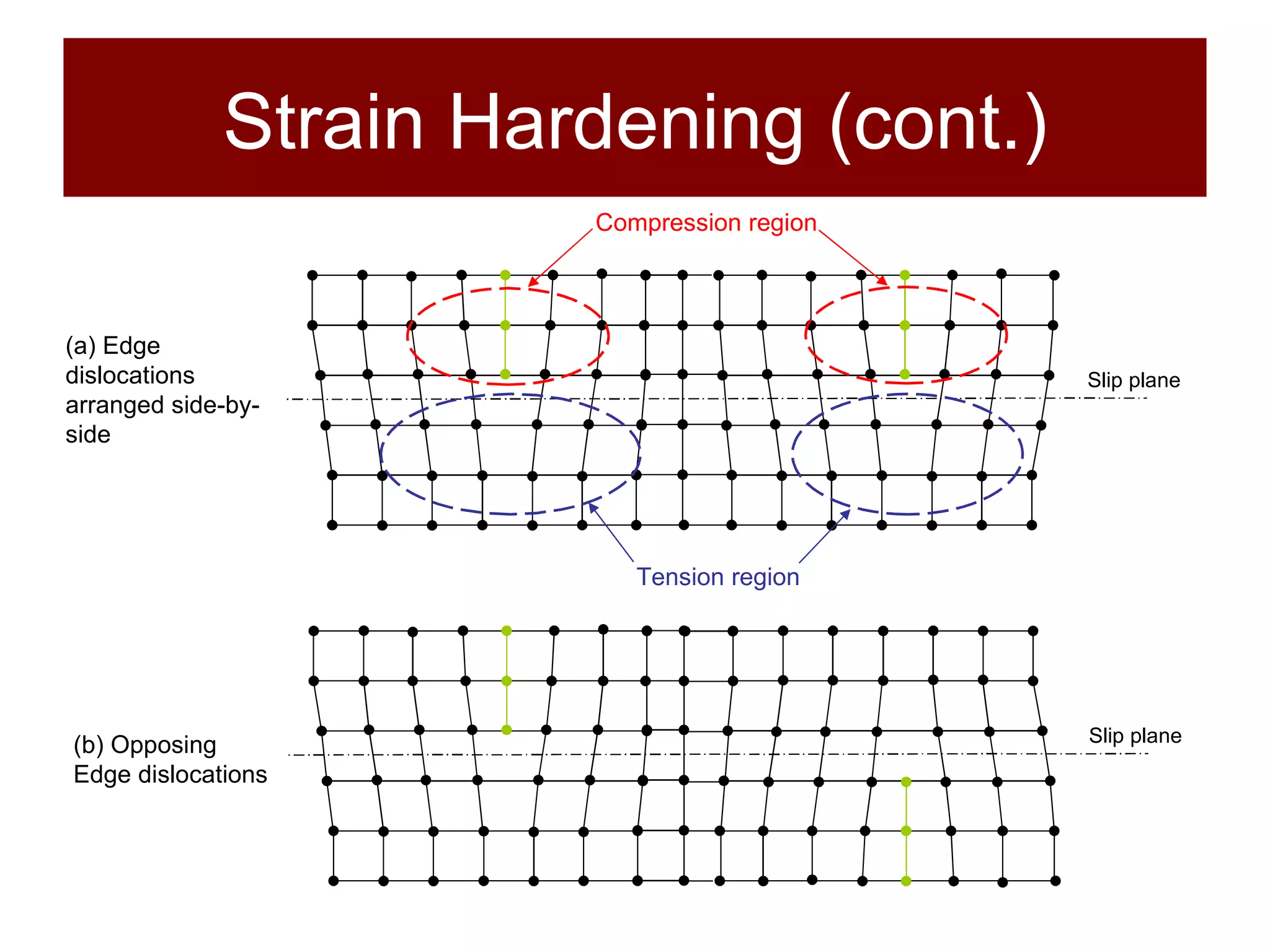
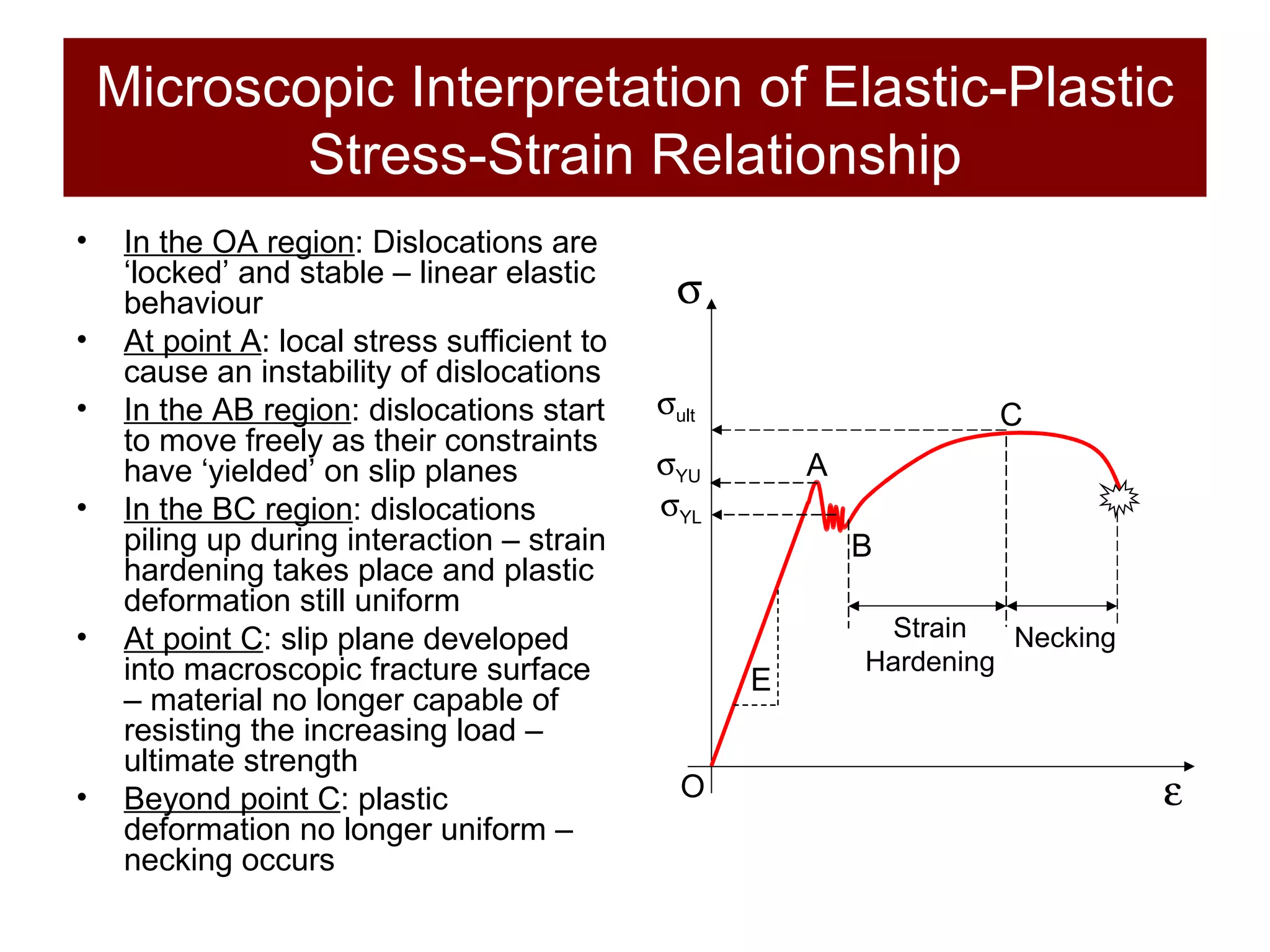
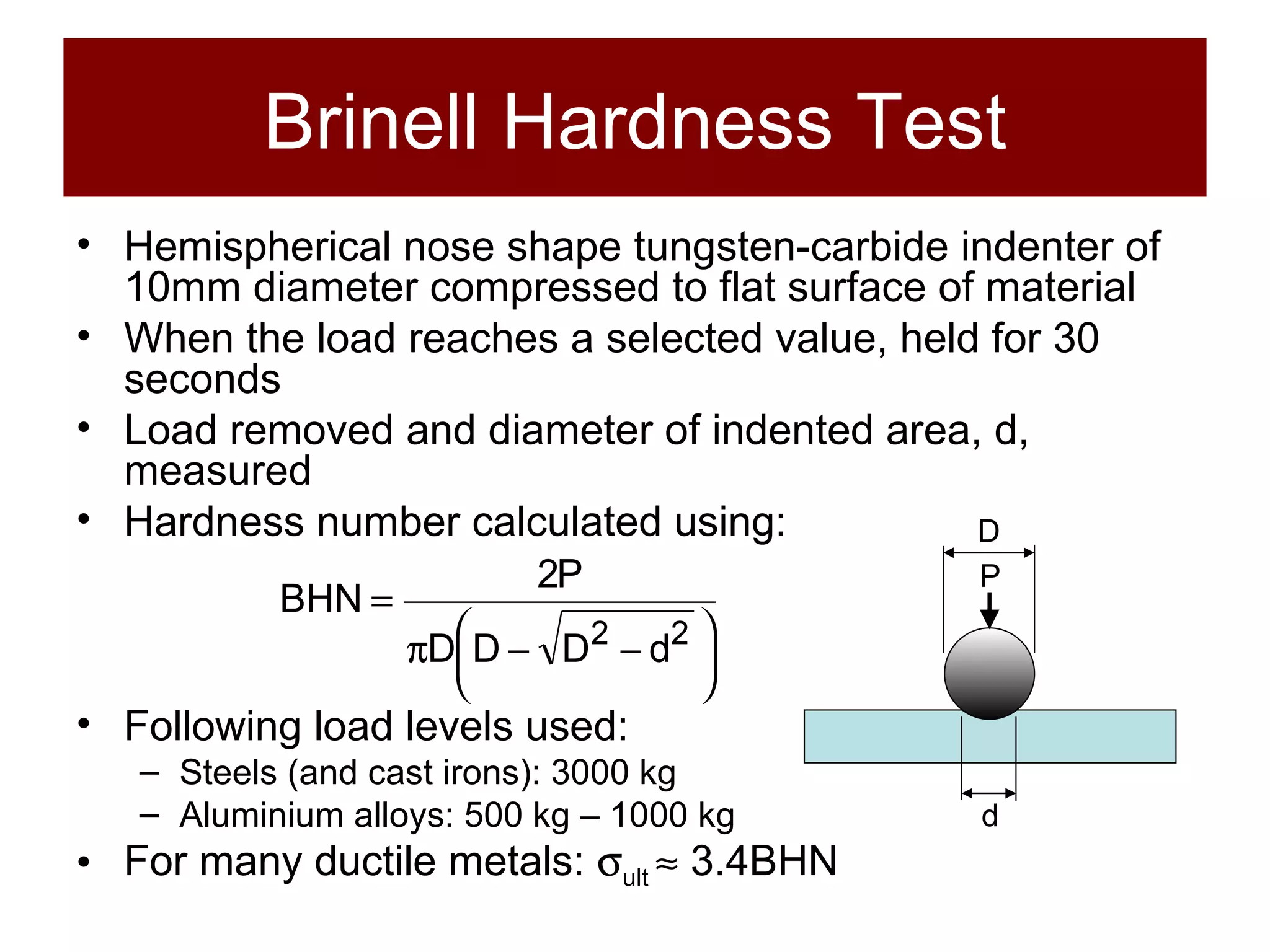
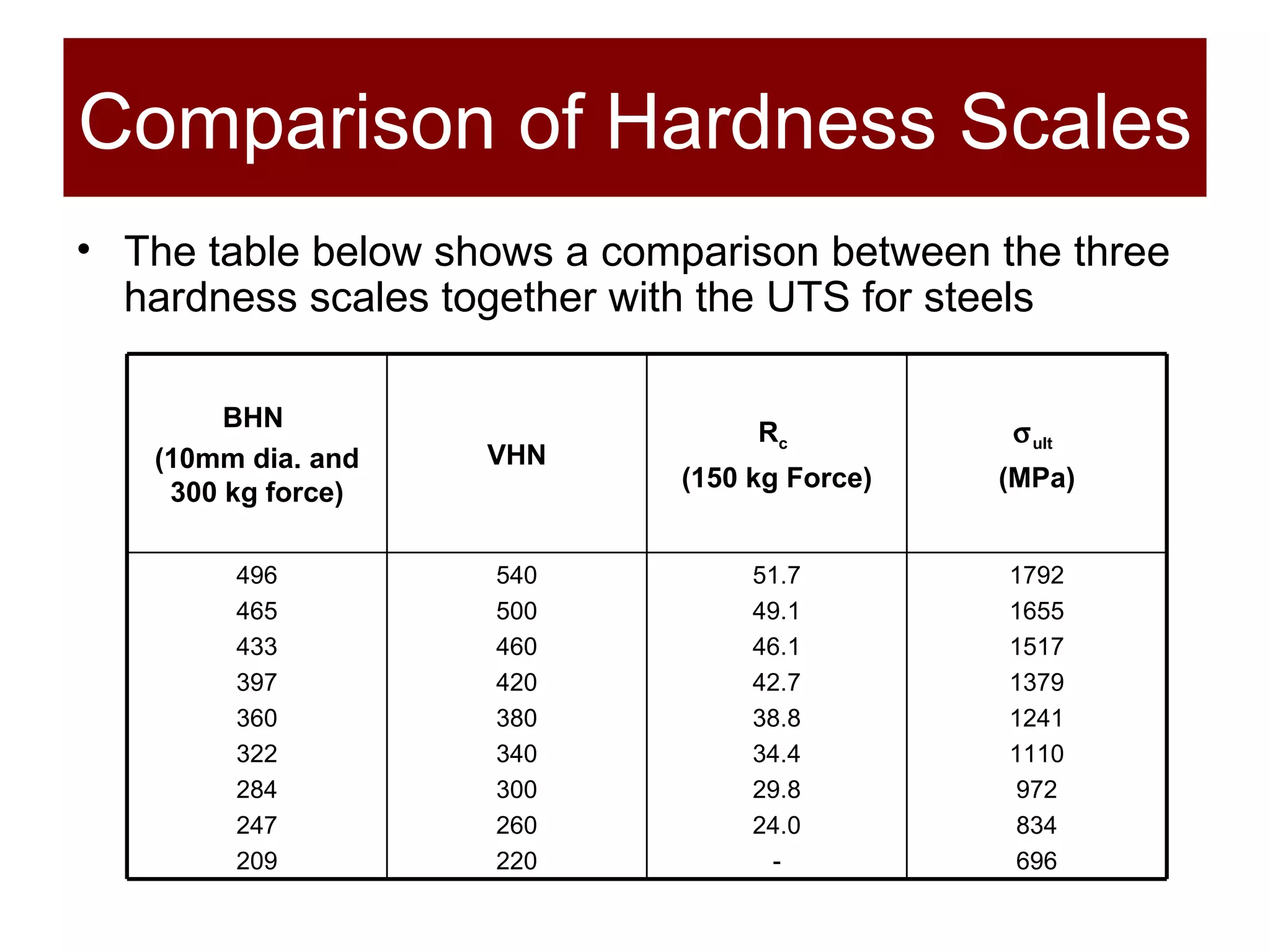
The document discusses the behavior of materials under stress and strain, introducing concepts like elastic and plastic deformation and detailing the micro-structure of materials, particularly polycrystalline materials. It explains stress-strain relationships, including true stress and strain definitions, and various hardness testing methods. Additionally, it covers the implications of dislocations and imperfections in solids on material behavior, ultimately highlighting the importance of mechanical properties in structural design.

1. Section 4 Behaviour of Materials The section will cover the behaviour of materials by introducing the stress-strain curve. The concepts of elastic and plastic deformation will be covered. This will then lead to a discussion of the micro-structure of materials and a physical explanation of what is happening to a polycrystalline material as it is loaded to failure. © Loughborough University 2010. This work is licensed under a Creative Commons Attribution 2.0 Licence .

2. Contents Introduction Elasticity Plasticity Elastic-Plastic Stress-Strain Relationship Elastic-Plastic Stress-Strain Curves Secant and Tangent Modulii Unloading Modulus and Plastic Strain True Stress and Strain True Stress-Strain Curve Constant Volume Concept True Stress and Strain Relationships Ductility Index Imperfections in Solids Line Defects or Dislocations Dislocation Movement and Strain Hardening Microscopic Interpretation of Elastic-Plastic Stress-Strain Relationship Hardness Credits & Notices

3. Introduction Knowledge of a material’s properties, and how it behaves under various loading conditions is essential in design Materials are selected for specific applications dependent on their properties and characteristics The behaviour of a material under load is markedly different depending on whether the material response is elastic or plastic

4. Elasticity For the tensile bar, the external load has been assumed to be low enough that the bar will resume its initial shape once the external load is removed This state of elastic deformation is possible only when the external load is within certain limits In the elastic range, the load-displacement or stress-strain curve is linear – loading and unloading follow the same path Elastic limit   Loading Unloading E

5. Plasticity If the loading is increased, it will reach a certain limit whereby elastic deformation would end and plastic deformation would start This limit is known as the elastic limit and beyond this point the material is said to have yielded The loading is thus beyond the elastic limit Permanent or irreversible deformation Stress corresponding to yielding is called the yield strength , denoted by  y Elastic limit   Loading Unloading E Point of yielding  y

6. Elastic-Plastic Stress-Strain Relationship Linear elastic stress-strain relationship considered thus far Knowledge of mechanical behaviour in plastic region also important in structural design / stress analysis Complex plastic behaviour dependent on nature of material Complete elastic-plastic stress strain relationship can be categorised by two types: Distinct yielding, i.e. mild steels, low / medium carbon steels Less distinct yielding, i.e. aluminium alloys, alloy steels

7. Elastic-Plastic Stress-Strain Curves Low / Medium Carbon Steels Aluminium Alloys and Alloy Steels  ult = Ultimate Strength  YU = Upper yield point  YL = Lower yield point  pr = Proof stress   0.1% 0.2% 0.1%  pr 0.2%  pr  ult Limit of Proportionality    YU  YL  ult E Strain Hardening Necking

8. Secant and Tangent Modulii Some materials (cast iron, concrete) do not have a linear elastic portion of the stress-strain curve For this nonlinear behaviour, Secant and Tangent Modulii are used Secant modulus: Slope of straight line between origin and a point on stress-strain curve Tangent modulus: Slope of the stress-strain curve at a specified level of stress    1  2

9. Unloading Modulus and Plastic Strain Unloading path is often linear Slope of an approximate straight unloading line defined as the unloading modulus Plastic or permanent deformation calculated from knowledge of total strain  p  e   0.1%  pr E sec

10. Example 4.1 A steel tensile specimen has a diameter of 10mm and a Young’s modulus of 209GPa. The load corresponding to 0.2% strain limit is 7kN and the maximum load recorded is 10kN with a total strain of 10%. Determine (i) the yield strength, (ii) the ultimate strength, and (iii) the plastic strain at the maximum load. Answer: (i)  y =89 MPa (ii)  ult =127 MPa (iii)  p =9.94%

11. True Stress and Strain True Stress: a stress defined with respect to the current or true cross-sectional area, A true as In the plastic range, plastic deformation or permanent reduction in cross-sectional area is significant A continuous use of nominal or engineering stress is no longer accurate

12. True Stress-Strain Curve   Onset of necking True Stress-Strain Curve Corrected for complex stress state in the neck region Engineering Stress-Strain Curve A true P x P x P x P x A

13. Constant Volume Concept A volume change in the elastic range is extremely small and is regarded as negligible In the plastic range, plastic deformation occurs through shear and thus no volume change takes place Thus we can write: This constant volume concept gives the following:

14. True Stress and Strain Relationships True stress-engineering stress relationship: True strain defined by: True strain-engineering strain relationship:

15. Ductility Index In order to estimate the ability of a metal to deform plastically, the ductility index is used as a measure: The ductility index is related to true stress and strain by:

16. Example 4.2 A steel tensile specimen has a diameter of 5mm and a gauge length of 100mm. During loading, a sampling pair of data points was taken at 10kN with a new length of 102mm. Determine (i) the true stresses and true strains at the sampling load, (ii) the corresponding diameter, and (iii) the ductility index at the sampling load. Answer: (i)  true =519 MPa,  true =0.0198 (ii) d´=4.95 mm (iii) q=1.93%

17. Imperfections in Solids Metallic materials are made up of millions of crystals with BCC, FCC, or HCP crystal microstructures These crystal microstructures are not perfect in their atomic arrangement – they contain inherent structural defects Defects exist in metals in the form of line defects or point defects in the crystal structure during the solidification process Line defects are commonly known as dislocations BCC FCC HCP

18. Line Defects or Dislocations Dislocations exist in the crystal lattice in the shape of plane (3D space) or line (2D space) Dislocations should not be interpreted as an indication of poor material quality Two types of dislocation are identified Edge dislocation Screw dislocations

19. Edge Dislocations Stress Stress Stress Stress Stress Stress Slip plane Burgess vector, b

20. Screw Dislocations Dislocations that produce the same result (plastic deformation) but the slip plane is parallel to the line of dislocation The magnitude and direction of the lattice distortion with a dislocation is expressed in terms of a Burgess vector, b Burgess Vector Dislocation Line

21. Point Defects Point defects are localised defects in the crystal microstructure involving one ore more atoms Caused by manufacture or heat treatment Three point defect types: vacancy, interstitial and substitutional Vacancy Interstitial Substitutional

22. Dislocation Movement and Strain Hardening Metals and alloys contain thousands of crystal grains and many dislocations The existence of dislocations creates local strain or stress fields. Upon loading, local strain or stress fields intensify Local yielding occurs at front of dislocations Atomic bonds break Dislocations start moving or slipping across crystal planes – plastic deformation Dislocations interact among themselves and with grain boundaries / point defects Dense concentration of dislocations occurs – pile-up Resistance to external load increases – strain hardening

23. Strain Hardening (cont.) (a) Edge dislocations arranged side-by-side (b) Opposing Edge dislocations Tension region Slip plane Compression region Slip plane

24. Microscopic Interpretation of Elastic-Plastic Stress-Strain Relationship In the OA region : Dislocations are ‘locked’ and stable – linear elastic behaviour At point A : local stress sufficient to cause an instability of dislocations In the AB region : dislocations start to move freely as their constraints have ‘yielded’ on slip planes In the BC region : dislocations piling up during interaction – strain hardening takes place and plastic deformation still uniform At point C : slip plane developed into macroscopic fracture surface – material no longer capable of resisting the increasing load – ultimate strength Beyond point C : plastic deformation no longer uniform – necking occurs    YU  YL  ult E Strain Hardening Necking O C B A

25. Hardness Hardness test result used to quickly assess degree of yielding , ductility , strain-hardening , or ultimate strength Hardness generally considered as resistance to permanent or plastic deformation Hardness test carried out by static indentation Measured hardness number Thickness of specimen must be 10  the indentation produced at the end of the test Three major test methods: Brinell Vickers (popular in UK) Rockwell (popular in US)

26. Brinell Hardness Test Hemispherical nose shape tungsten-carbide indenter of 10mm diameter compressed to flat surface of material When the load reaches a selected value, held for 30 seconds Load removed and diameter of indented area, d, measured Hardness number calculated using: Following load levels used: Steels (and cast irons): 3000 kg Aluminium alloys: 500 kg – 1000 kg For many ductile metals:  ult  3.4BHN D d P

27. Vickers Hardness Test Indenter is a square-based diamond pyramid The angles between the opposite faces of the pyramid are 136  The surface diagonal of the pyramidal indent is measured when the load reaches a selected level Harness number calculated as: The selected load levels are: Steels (and cast irons): 30 kg Aluminium Alloys: 5 kg d P L L

28. Rockwell Hardness Test A load P is applied to the flat surface of a material. Once the load reaches the selected load level, the indentation depth is measured with a dial test indicator (DTI) Hardness number is found by using a look-up table No calculation is required For most metals, Rockwell C or R c is used with the selected load level of 150 kg

29. Comparison of Hardness Scales The table below shows a comparison between the three hardness scales together with the UTS for steels BHN (10mm dia. and 300 kg force) VHN R c (150 kg Force)  ult (MPa) 496 465 433 397 360 322 284 247 209 540 500 460 420 380 340 300 260 220 51.7 49.1 46.1 42.7 38.8 34.4 29.8 24.0 - 1792 1655 1517 1379 1241 1110 972 834 696

30. This resource was created by Loughborough University and released as an open educational resource through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme. © 2010 Loughborough University. Except where otherwise noted this work is licensed under a Creative Commons Attribution 2.0 Licence . The name of Loughborough University, and the Loughborough University logo are the name and registered marks of Loughborough University. To the fullest extent permitted by law Loughborough University reserves all its rights in its name and marks, which may not be used except with its written permission. The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England & Wales Licence. All reproductions must comply with the terms of that licence. The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only, provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher. Credits