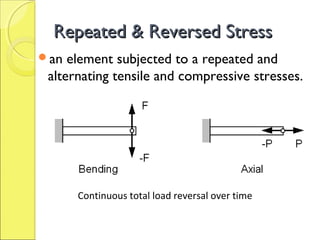
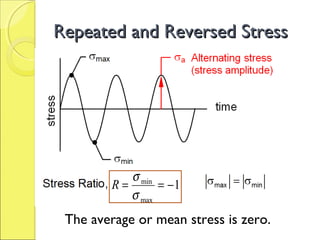
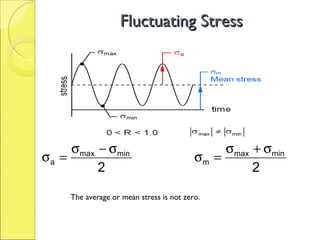
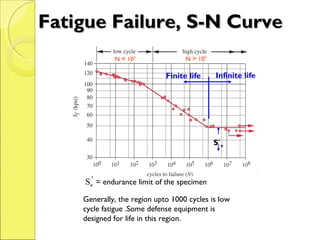
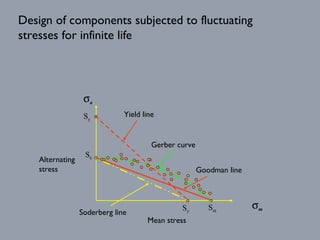
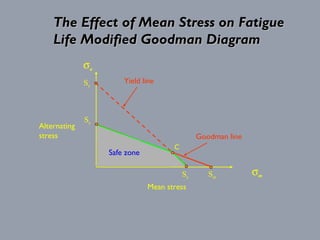
The document discusses the effects of fluctuating stresses on material fatigue in mechanical design, highlighting the differences between cyclic loading and mean stresses. It defines key concepts such as fatigue life, fatigue strength, and endurance limit, providing formulas for calculating these parameters in design applications. Examples illustrate how to determine component dimensions based on fluctuating stress conditions and material properties.

1. FLUCTUATING STRESSESFLUCTUATING STRESSES
SUBJECT: Machine Design
Mechanical Engineering Department
Presented by: Flt Lt Dinesh Gupta
Associate Professor
Deptt. Of Mech. Engg.
NIET, Alwar (Raj.)

2. Fatigue loadFatigue load
• Reduced material resistance under
fluctuating stresses or reversals,
which may culminate in cracks or
failure after a number of cycles.
Fatigue is the tendency of a
member to fail at stress levels below
yield stress when subject to cyclical
loading.
Therefore failure criterion is not
yield stress or ultimate tensile
stress.Then what is that?

5.  Completely reversed cycle of
stress:
 Illustrates the type of fatigue
loading where a member is
subjected to opposite loads
alternately with a means of zero.
 For example bending of steel wire
continuously in either direction
leads to alternate tensile and
compressive stresses on its
surface layers and failure fatigue.

6. Repeated & Reversed StressRepeated & Reversed Stress
an element subjected to a repeated and
alternating tensile and compressive stresses.
Continuous total load reversal over time

7. Repeated and Reversed StressRepeated and Reversed Stress
The average or mean stress is zero.
1
max
min
−==
σ
σ
R

8. Definitions:Definitions:
22
minmax σσσ
σ
−
=
∆
=a
2
minmax σσ
σ
+
=m
max
min
σ
σ
=R R = 0, repeated and one direction, i.e. stress
cycles from 0 to max value.
R =-1, Fully reversed
= Alternating stress
= Mean stress

9. Fluctuating StressFluctuating Stress
When an element experiences alternating
stress, but the mean stress is NOT zero.
Load varies between P and Q over time

10. Fluctuating StressFluctuating Stress
2
minmax
a
σ−σ
=σ
2
minmax
m
σ+σ
=σ
The average or mean stress is not zero.

11.  Fatigue properties :
 Fatigue life (N): it is total number
of cycles are required to bring
about final fracture in a specimen
at a given stress.
 Fatigue life for a given condition is
a property of the individual
specimen and is arrived at after
testing a number of specimens at
the same stress.

12. Fatigue strength (σn)
 It is the maximum stress at which
a material can withstand
repeatedly N number of cycles
before failure.
 OR it is the strength of a material
for a particular fatigue life.

13. Fatigue limit or Endurance limit
(Se ’):
it is stress below which a material
will not fail for any unlimited
number of cycles.
For ferrous materials it is
approximately half of the ultimate
tensile strength.
This value is obtained with the help
of standard rotating beam test.

14. Endurance limit
The cyclic stress level that the material
can sustain for 10 million cycles is called
the Endurance Limit (EL).Denoted by Se’.
Rotating-beam specimen (Bending)
For Steels,
Se’ = 0.5 Sut, Sut ≤ 1400 MPa
For Cast iron and cast steels,
Se’ = 0.45 Sut MPa, Sut ≤ 600 MPa

15. The endurance limit of a real machine
component is lower than the estimated
of experimentally determined endurance
limit because the size, shape, surface
finish, etc of a components are generally
quite different from those of the
specimens used in testing. As such the
following relationship is generally used to
determine endurance strength of real
component.
Se = Ka Kb Kc Kd Ke Se’

16. Se = endurance strength of a component, MPa
Se’ = endurance limit of a standard specimen of
the respective material in a rotating beam
machine.
Ka = surface finish factor
Kb = size factor
Kc = reliability factor
Kd = modifying factor for stress concentration
Ke = miscellaneous factor like temperature,
environmental etc

17. Fatigue Failure, S-N CurveFatigue Failure, S-N Curve
Finite life Infinite life
N < 103
N > 103
S′e
= endurance limit of the specimenSe
′
Generally, the region upto 1000 cycles is low
cycle fatigue .Some defense equipment is
designed for life in this region.

18. Mean stress
Alternating
stress
σm
σa
Se
Sy
Soderberg line
Sut
Goodman line
Gerber curve
Sy
Yield line
Design of components subjected to fluctuating
stresses for infinite life

19. The Effect of Mean Stress on FatigueThe Effect of Mean Stress on Fatigue
Life Modified Goodman DiagramLife Modified Goodman Diagram
Mean stress
Alternating
stress
σm
σa
Sut
Goodman line
Sy
Yield line
Sy
Se
Safe zone
C

21. Example on reversed stressExample on reversed stress
1. A plate made of steel 20C8 Sut=440N/mm2. It is subjected to a
completely reversed axial load of 30KN. Assume ka=0.67,
kb=0.85, kc=0.89, kd=0.45 and factor of safety as 2. Determine
the plate thickness for infinite life?
Sol. Se’=0.5 Sut=0.5x440=220N/mm2
Se=KaxKbxKcxKdxSe’=0.67x0.85x0.89x0.45x220=50.9N/mm2
Allowable stress= Se/fs=50.9/2=25.45N/mm2
Also allowable stress= P/(w-d)t=(30x1000)/(50-10)t=25.45
t=29.47mm

22. Example on fluctuating stressExample on fluctuating stress
1. A circular rod made of ductile material has endurance strength of
280N/mm2 and ultimate strength of 350N/mm2. The member is
subjected to variable axial load varying from 300KN(tensile) and
70KN(compressive). Assume Ka=0.85, Kb=1.0, Kc=1,Kd=0.55 and
factor of safety as 2. Find suitable diameter of the rod?
Sol. Se’=280N/mm2
Sut=350N/mm2
Using Goodman line equation:
Sm/Sut + Sa/Se=1/fs……………………(1)
Se=KaxKbxKcxKcxKdxSe’=0.85x1x1x0.55x280=132.3MPa
Sm=(Pmax+Pmin)/2A=[300+(-70)]/2A=115/A N/mm2
Sa=(Pmax-Pmin)/2A=[300-(-70)]/2A=185/A N/mm2
Put values in eqn. 1 we get: A= 3456mm2
Now A= π/4 d2=3456 or d=66.3mm

23. THANK YOUTHANK YOU