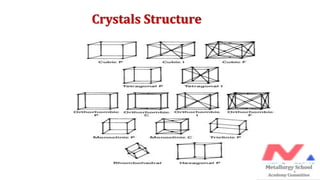
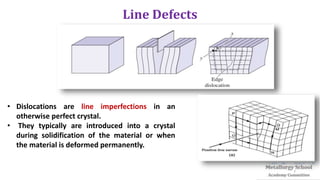
The document presents foundational concepts in metallurgy, focusing on crystalline and amorphous materials, crystal defects, and the mechanisms of plastic deformation. It discusses dislocations, their types, and how they influence the mechanical properties of materials, particularly in relation to yield strength and slipping mechanisms. The text also explores theories related to work hardening and the impact of solute atoms on dislocation behavior.

1. 1
First Session
Metallurgy School
Presented By:
Ahmed M. El-Naml
Edited By:
Nouran M. El-shaer
Academy Committee

2. 2

3. Crystalline And Amorphous Materials.
3
• Any material that exhibits only a short-range order of
atoms or ions is an amorphous material
• the atoms or ions in these materials form a regular
repetitive, grid-like pattern, in three dimensions. We refer
to these materials as crystalline materials.
• If a crystalline material consists of only one large crystal,
we refer to it as a single crystal.
• A polycrystalline material is composed of many small
crystals with varying orientations in space. These smaller
crystals are known as grains. The borders between
crystals, where the crystals are in misalignment, are
known as grain boundaries

4. 4
Crystals Structure

5. Crystal Defects
5
Grain Boundary
Twin Boundary
• All real crystals contain imperfections
which may be point, line, surface or
volume defects, and which disturb
locally the regular arrangement of the
atoms.
• Their presence can significantly
modify the properties of crystalline
solids

6. Point Defects:-
Vacancies And Interstitial.
6

7. Line Defects
7
• Dislocations are line imperfections in an
otherwise perfect crystal.
• They typically are introduced into a crystal
during solidification of the material or when
the material is deformed permanently.

8. Elastic Vs. Plastic Deformation
8
 Plastic deformation refers to irreversible
deformation or change in shape that occurs
when the force or stress that caused it is
removed.
 Plastic deformation is to be distinguished from
elastic deformation, which is a temporary
change in shape that occurs while a force or
stress remains applied to a material.
 In elastic deformation, the shape change is a
result of stretching of interatomic bonds, and
no dislocation motion occurs

9. Theoretical And Experimental Yield Strength Of crystals
9
• The stress required for this process can be
estimated and is of the order of one fifth of the
shear modulus of the crystal. The yield strength
predicted this way for metallic single crystals is
thus between 1 GPa and 25 GPa.
• If we measure the strength of single crystals of
pure metals, the values found are several orders of
magnitudes below this theoretical value and even
lie below that of engineering alloys.
• The reason for this spectacular failure of the
theoretical prediction is that plastic deformation
does not occur by sliding of complete layers of
atoms.
• Instead, it proceeds by a mechanism that is based
on a special type of lattice defect, the dislocations.

10. - Characteristics Of Dislocation.
- Dislocation Line And Burger vector.
10
Screw Dislocation
Mixed Dislocation
A dislocation can be described by two
vectors. The first is the line vector t, the
vector pointing in the direction of the
dislocation line.
The second vector is the Burgers vector b
Burgers vector .
Burgers vector :The direction and distance
that a dislocation moves in each step.

11. Edge, Screw And Mixed Dislocation
11
Edge dislocation:-
A dislocation introduced into the crystal
by adding an “extra half plane” of atoms.
Screw dislocation:-
A dislocation produced by skewing a
crystal by one atomic spacing so that a
spiral ramp is produced.

12. Dislocation Motion
12

13. Dislocation Loop
And
Prismatic Dislocation
13
Prismatic Loop
• If a dislocation forms a loop in a plane and b lies in
that plane the plane is the slip plane and the loop
can expand or shrink by glide, depending on the
forces acting on it .
• When the Burgers vector is not in the plane of the
loop, the glide surface defined by the dislocation
line and its Burgers vector is a cylindrical surface .
The dislocation is called a prismatic dislocation.
• It follows that the dislocation can only move
conservatively, i.e. by glide, along the cylindrical
surface and if the loop expands or shrinks climb
must be occurring

14. Resolve Stress of Single Crystal
14
The resolved shear stress is the stress component
acting as shear stress on the considered slip system
in the slip direction. If we restrict ourselves to the
case of uniaxial loading as in a tensile test, the
calculation of this component is not too difficult.

15. Critical Resolved Shear Stress (P-N)Stress.
15
• Critical resolved shear stress The shear
stress required to cause a dislocation to
move and cause slip.
• The Peierls--Nabarro stress represents the
resistance that the crystalline lattice
offers to the movement of a dislocation
• Typically, there is a preferred plane, and
in that plane there are specific directions
along which dislocation motion occurs

16. Slip Systems
• The slip system depends on the crystal structure of the
metal and is such that the atomic distortion that
accompanies the motion of a dislocation is a minimum.
• For a particular crystal structure, the slip plane is the
plane that has the densest atomic packing—that is, has
the greatest planar density.
• The slip direction corresponds to the direction in this
plane that is most closely packed with atoms—that is,
has the highest linear density.
16

17. Slip System = Planes & Directions.
17

18. Influence Of Crystal Structure.
18

19. Mechanical Twining
• Besides dislocation movement, there are other mechanisms of plastic
deformation. These are the martensitic transformation, diffusion creep at
high temperatures and finally the so-called twinning.
• Mechanical twinning usually contributes only slightly to plastic
deformation and is in general more difficult to activate than dislocation
movement.
• Mechanical twinning mainly occurs at low temperatures and in metals with
a small number of slip systems i. e., when slip of dislocation is difficult.
• The hexagonal metals show a greater tendency to form twins. Mechanical
twinning is a shear deformation of the lattice in which atoms are shifted
parallel to the so-called twinning plane,
19

20. Slipping & Twinning
20

21. Dislocation Motion
Conservative And Non-conservative.
21
• There are two basic types of dislocation movement.
Glide or conservative motion occurs when the
dislocation moves in the surface which contains both
its line and Burgers vector: a dislocation able to
move in this way is glissile, one which cannot is
sessile.
• Climb or non-conservative motion occurs when the
dislocation moves out of the glide surface, and thus
normal to the Burgers vector.
• Glide of many dislocations results in slip, which is the
most common manifestation of plastic deformation
in crystalline solids

22. Cross Slip VS. Climb
22
Cross Slip Climb
Edge dislocation can leave their slip
plane by another mechanism, the
thermally activated climb process.
During climb, the dislocation either
incorporates vacancies or emits them.
The dislocation thus moves
perpendicularly to its slip plane.
Cross-slip A change in the slip system
of a dislocation

23. Stress Field Of Edge & Screw Dislocation
σ 𝟏𝟏 = −
𝐆𝐛
𝟐𝛑 𝟏 − 𝐕
.
𝐱 𝟐(𝟑𝐱 𝟏
𝟐
+ 𝐱 𝟐
𝟐
)
𝐱 𝟏
𝟐
+ 𝐱 𝟐
𝟐 𝟐
σ 𝟐𝟐 =
𝐆𝐛
𝟐𝛑 𝟏−𝐕
.
𝐱 𝟐(𝐱 𝟏
𝟐
− 𝐱 𝟐
𝟐
)
𝐱 𝟏
𝟐+𝐱 𝟐
𝟐 𝟐
т 𝟏𝟐 =
𝐆𝐛
𝟐𝛑 𝟏−𝐕
.
𝐱 𝟏(𝟑𝐱 𝟏
𝟐
− 𝐱 𝟐
𝟐
)
𝐱 𝟏
𝟐+𝐱 𝟐
𝟐 𝟐
23
• Because dislocations distort the crystal
lattice, an elastic stress field forms around
the dislocation line

24. Strain Energy Of Edge & Screw
Dislocation
• ѡ 𝒆 = 𝒓 𝟎
𝒓’
(
𝞵𝒃
𝟐𝝅𝒓
) 𝟐 𝟏
𝟐𝞵
𝟐𝝅𝒓 𝒅𝒓 =
𝞵𝒃 𝟐
𝟒𝝅
𝐥𝐧
𝒓’
𝒓 𝟎
• ѡ 𝒆 =
𝞵𝒃 𝟐
𝟒𝝅(𝟏−𝒗)
𝐥𝐧
𝟒𝒓’
𝒃
24
Because the dislocation elastically deforms the lattice in its vicinity, elastic energy is
stored here.
The more dislocations there are in a crystal, the higher its stored elastic energy.

25. Low Angle Grain Boundary.
(Tilt Boundary)
Interaction Of Dislocation
25
These boundaries can be described in terms
of dislocation arrays.
One simple small-angle grain boundary is
formed when edge dislocations are aligned
in the manner of the Figure.

26. Dislocation Density
26
To achieve the theoretical strength of a crystalline lattice, there are two possible
methods:
(1) eliminating all defects and
(2) creating so many defects, that their interactions render them inoperative. The first
approach has yielded some materials with extremely high strength. Unfortunately, this
has been possible only in special configurations called ‘‘whiskers.”

27. Dislocation Multiplication
• Frank Read Source
• Multiply Cross Slip.
27

28. Slip Bands
28
Slip band is a Collection of many slip lines, often easily visible.

29. Orwan Mechanism Of Hardening.
29

30. Dislocation Observation
30
Transmission image
Pitting method
Etch pits Holes created at locations where
dislocations meet the surface. These are used
to examine the presence and density of
dislocations.

31. Perfect Dislocation And Partial
Dislocation
31
When a perfect dislocation decomposes itself into partials, a region of
faulty stacking is created between the partials

32. Frank’s Rule
32
In most metals, each dislocation in Fig
will be dissociated in its glide plane into
two Shockley partial dislocations
bounding a stacking-fault ribbon .

33. Stacking Fault Energy
33
Extended Dislocation

34. Sessile Dislocation
34
Lomer-Cottrell Sessile Interaction
If the dislocations meet at the
line of intersection of the two
planes, the leading partials
repel or attract each other
according to Frank’s rule for
their Burgers vectors.

35. Jog And Kick
35
• Kinks and jogs create edge-like
segments in screw dislocations
and vice versa.
• The length of the dislocation
grows in many configurations by
one Burgers vector of the other
dislocation.

36. Dislocation Velocity
36

37. Dislocation Intersection
37

38. 38
Dislocation Intersection : cont;

39. Dislocation Pile-Ups
39
All dislocations generated by a Frank--Read
source are in the same slip plane if they do not
cross-slip.
Each dislocation in a pileup is in equilibrium
under the effect of the applied stress and of
the stresses due to the other dislocations (in
the pileup)

40. Solute Atom Dislocation Interactions
• When a crystal contains both dislocations and solute atoms, interactions
may occur. Of particular interest is the interaction between substitutional
solutes and dislocations in the edge orientation.
• These distortions may be largely relieved if the solute atom finds itself in
the proper place close to the center of a dislocation. Thus, the free
energy of the crystal will be lowered when a small solute atom is
substituted for a larger solvent atom in the compressed region of a
dislocation in, or close to, the extra plane of the dislocation.
40

41. 41
Yielding Phenomenon

42. Introduction To Work Hardening
Theory
42
• Taylor’s Theory
• Seeger’s Theory
Strain hardening is the phenomenon by which
a ductile metal becomes harder and stronger
as it is plastically deformed.
During plastic deformation, the number of
dislocations increases dramatically.
the ability of a metal to deform plastically
depends on the ability of dislocations to
move.

43. In brief, this approach assumes that if the
dislocation density is expressed in numbers
of dislocations intersecting a unit area, then
the average distance between dislocations is
proportional to r1/2
𝝉=K𝝆
𝟏
𝟐
Orwon Equation:-
𝜸 = 𝝆𝒃 𝒗 43
Taylor’s Relation:-