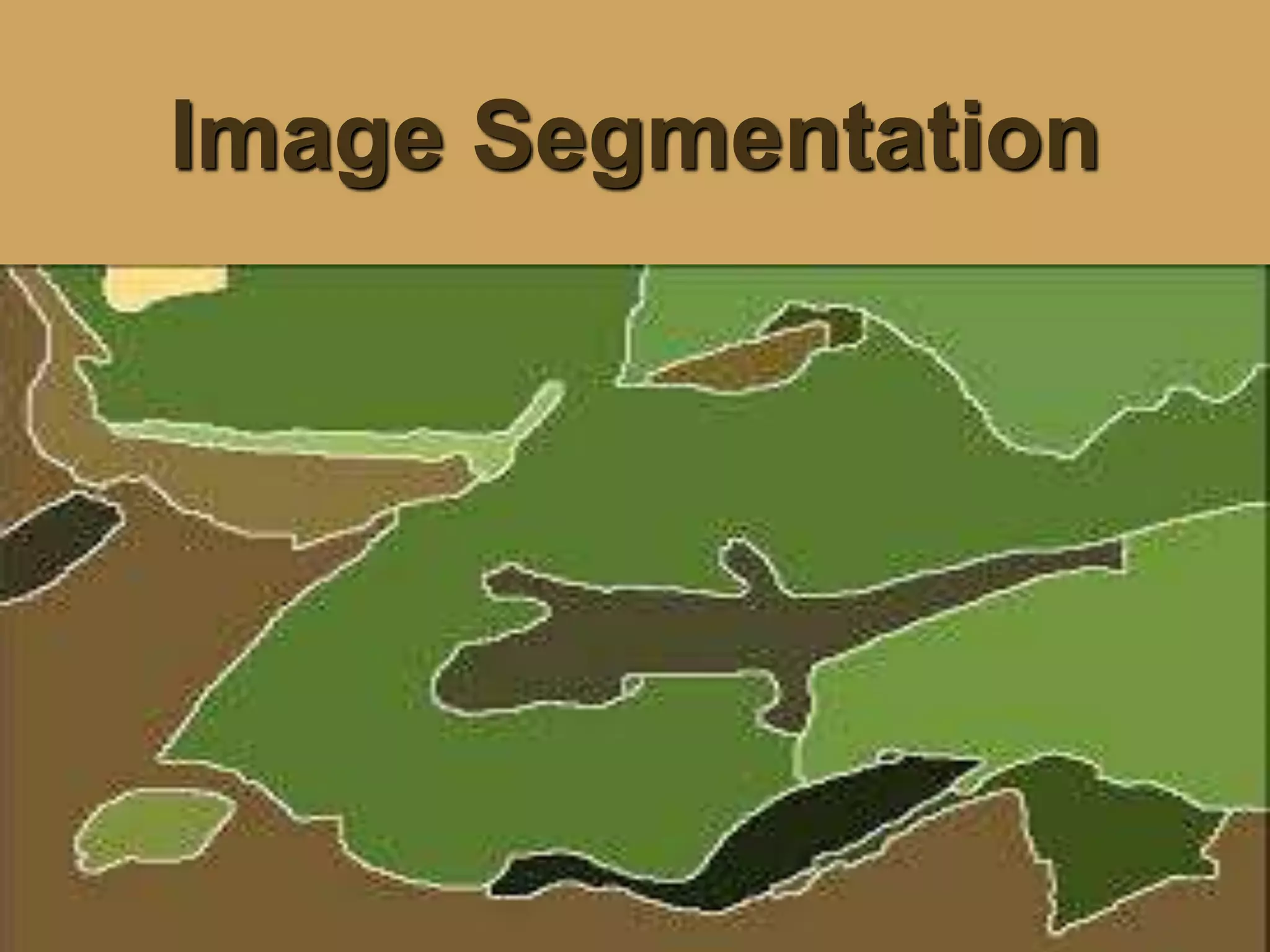
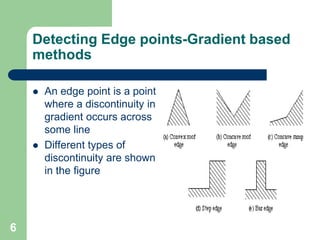
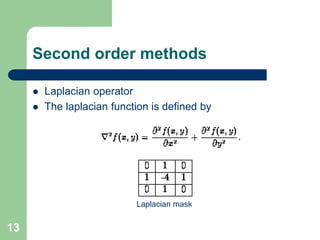
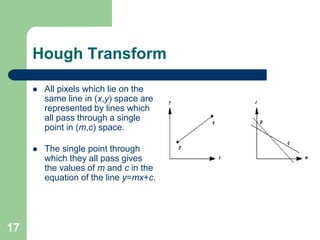
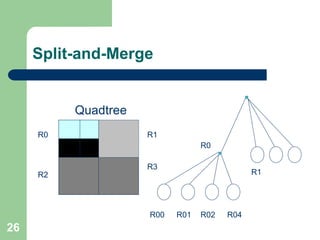
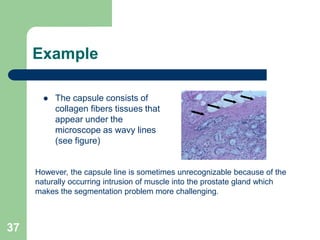
The document discusses various methods of image segmentation, which is the process of partitioning an image into homogenous regions. It covers edge-based and region-based segmentation techniques such as region growing and split-and-merge, as well as active contour models (snakes) and their applications in medical imaging. The conclusion emphasizes the complexity of image analysis in medical contexts and the necessity of incorporating prior knowledge to improve segmentation outcomes.

1. 1
Image Segmentation

2. 2
Outline
 Introduction
 Edge-based segmentation
 Region-based segmentation
– Region Growing
– Split-and-merge
 Active contour models (snakes)
 Application in medical imaging
 Conclusion
 Assignment 2

3. 3
Introduction
 What is Image segmentation ?
– The different partitioning of an image into non-
overlapping, constituent regions which are
homogeneous with respect to some characteristic
such as intensity or texture.
– Each of such homogeneous regions may
represent an object.

4. 4
Introduction
The shape of an object can be described in terms of:
 Its boundary – requires image edge detection
 The region it occupies – requires image
segmentation in homogeneous regions, Image
regions generally have homogeneous
characteristics (e.g. intensity, texture)
 Segmentation methods are then classified into
– Edge-based
– Region-based

5. 5
Edge-based Segmentation
 Emphasis:
– Determine the boundaries that separate regions
 Common approaches
– Find edge points in the image
 Gradient based methods
 Second order methods
– Linking these points in some way to produce
description of edges in terms of lines, curves etc

6. 6
Detecting Edge points-Gradient based
methods
 An edge point is a point
where a discontinuity in
gradient occurs across
some line
 Different types of
discontinuity are shown
in the figure

7. 7
Gradient based methods (cont.)
 The gradient is a vector whose components
measure how rapidly pixel values are changing
with distance, in the x and y directions

8. 8
Gradient based methods (cont.)
 Considering dx=dy=1 (pixel spacing) and considering
a point (i,j)
Δx = f(i+1,j) – f(i,j)
Δy = f(i,j+1) – f(i,j)
Δx and Δy can be calculated by convolving the image
with convolution masks

9. 9
Gradient based methods (cont.)
 To approximate the gradient along directions at 45o and 135o
to the axes respectively,
known as Roberts edge operator. The corresponding
convolution masks are
 Other 3x3 edge operators can be used such as Sobel and
Canny

10. 10
Example
Original image Image produced by
the horizontal
gradient calculation
Image produced by
the vertical gradient
calculation

11. 11
Example
Gradient image formed by combining horizontal
and vertical gradient detection
Gradient image is produced using
the magnitude M form
M = | Δx | + | Δy |
The gradient direction θ is equal
to
Θ = tan-1 (Δy / Δx )

12. 12
Implementation using Matlab
 Read image and display it.
I = imread('coins.jpg'); imshow(I)
 Apply the Sobel and Canny
edge detectors to the image
and display them
BW1 = edge(I,'sobel');
BW2 = edge(I,'canny');
imshow(BW1) figure,
imshow(BW2)
Original image “coins.jpg”

13. 13
Second order methods
 Laplacian operator
 The laplacian function is defined by
Laplacian mask

14. 14
Edge Linking
 Edge detectors yield pixels that lie on edges
 The objective is to replace many points on
edges with real edges.
 Edge linking can be performed by:
– Local edge linkers – where edge points are
grouped according to their relationships with the
neighboring edge points.
– Global Edge Linkers – Hough transform

15. 15
Hough Transform
 Allows recognition of global patterns in an
image
 Finds curves like straight lines, circles, etc
 Suppose that we are looking for straight lines
in an image
– If we take a point (x',y') in the image, all lines
which pass through that pixel have the form
y’ = mx’ +c

16. 16
Hough Transform
 This equation can be
written as
c = -x’m + y’
where x’,y’ are constants
and m,c varies
 Each different line
through the point (x',y')
corresponds to one of
the points on the line in
(m,c) space
Lines through a
point

17. 17
Hough Transform
 All pixels which lie on the
same line in (x,y) space are
represented by lines which
all pass through a single
point in (m,c) space.
 The single point through
which they all pass gives
the values of m and c in the
equation of the line y=mx+c.

18. 18
Hough Transform
 The y=mx+c form for representing a straight line
breaks down for vertical lines, when m becomes
infinite.
 To avoid this problem, it is better to describe straight
lines in the form of
x cos θ + y sin θ = r
i.e. a point in (x,y) space is now represented by a curve
in (r,θ) space rather than a straight line

19. 19
Hough Transform
 To detect straight lines in an image
1. Quantize (m,c) space into a two-dimensional array A for
appropriate steps of m and c.
2. Initialize all elements of A(m,c) to zero.
3. For each pixel (x',y') which lies on some edge in the image,
add 1 to all elements of A(m,c) whose indices m and c
satisfy y'=mx'+c.
4. Search for elements of A(m,c) which have large values --
Each one found corresponds to a line in the original image.

20. 20
Hough Transform
 To find circles, with equation
(x – a)2 + (y – b)2 = r2
– Every point in (x,y) space corresponds to a surface in (a,b,r) space
(as we can vary any two of a, b and r, but the third is determined
by the equation of the circle).
– The basic method is, thus, modified to use a three-dimensional
array A(a,b,r),
– All points in it which satisfy the equation for a circle are
incremented.
 The technique takes rapidly increasing amounts of time for
more complicated curves as the number of variables (and
hence the number of dimensions of A) increases

21. 21
Outline
 Introduction
 Edge-based segmentation
 Region-based segmentation
– Region Growing
– Split-and-merge
 Active contour models (snakes)

22. 22
Region Growing
 A simple approach to image segmentation is
to start from some pixels (seeds)
representing distinct image regions and to
grow them, until they cover the entire image
 Before assigning a pixel x to a region Ri(k),
check if the region is homogeneous: i.e.
H(Ri(k) U {x}) = TRUE

23. 23
Region Growing
 The arithmetic mean M and standard
deviation sd can be used to decide if merging
two regions R1,R2 is allowed
 if |M1 – M2| < (k)*sd(i) , i = 1, 2 , merge the
two regions
where k is a certain threshold

24. 24
Split-and-Merge
 The opposite approach to region growing is region
splitting.
 The approach starts with the assumption that the
entire image is homogeneous
 If the entire image is not homogeneous, the image is
split into four sub images
 This splitting procedure is repeated recursively until
the image is split into homogeneous regions

25. 25
Split-and-Merge
 Since the procedure is recursive, it produces
an image representation that can be
described by a tree whose nodes have four
children each
 Such a tree is called a Quadtree.

26. 26
Split-and-Merge
Quadtree
R0 R1
R2
R3
R0
R1
R00 R01 R02 R04

27. 27
Example
Image and a representation of its quadtree decomposition

28. 28
Split-and-Merge
 Splitting techniques create regions that may
be adjacent and homogeneous, but not
merged.
 Split and Merge method is an iterative
algorithm that includes both splitting and
merging at each iteration. It produces more
compact regions than the splitting algorithms

29. 29
Split-and-Merge Algorithm
 If a region R is inhomogeneous
(H(R)= False) then split into four sub regions
 If two adjacent regions Ri,Rj are
homogeneous (H(Ri U Rj) = TRUE), merge
them
 Stop when no further splitting or merging is
possible

30. 30
Outline
 Introduction
 Edge-based segmentation
 Region-based segmentation
– Region Growing
– Split-and-merge
 Active contour models (snakes)
 Application in medical imaging
 Conclusion

31. 31
Active Contour Models (Snakes)
 First introduced in 1987 by Kass et al, and gained
popularity since then.
 Represents an object boundary as a parametric
curve.
 An energy function E is associated with the curve.
 The problem of finding object boundary is an energy
minimization problem.

32. 32
Framework for snakes
 A higher level process or a user
initializes any curve close to the
object boundary.
 The snake then starts
deforming and moving towards
the desired object boundary.
 In the end it completely “wraps”
around the object.
(Digram courtesy “Snakes, shapes, gradient vector flow”, Xu, Prince)

33. 33
Snakes
 Contour possesses an energy (Esnake) which is defined as the
sum of the three energy terms.
where Einternal represents the internal energy of the spline due to
bending, Eexternal denotes image forces, and Econstraint denotes
external constraint forces.
 The energy terms are defined such that the final position of
the contour will have a minimum energy (Emin)
 Therefore the problem of detecting objects reduces to an
energy minimization problem.
int intsnake ernal external constraE E E E  

34. 34
Outline
 Introduction
 Edge-based segmentation
 Region-based segmentation
– Region Growing
– Split-and-merge
 Active contour models (snakes)
 Application in medical imaging
 Conclusion

35. 35
Application in medical imaging
 In-vivo segmentation: automating or facilitating the
delineation of anatomical structures and other
regions of interest
 Segmentation methods vary widely depending on
the specific application and imaging modality.
 There is currently no single segmentation method
that yields acceptable results for every medical
image.
 Selecting an appropriate approach to a
segmentation problem can be a difficult dilemma.

36. 36
Example
 In reconstructing a 3D
model of a prostate, the
capsule contour needs to
be extracted from the
slices’ images
Capsule contour

37. 37
Example
 The capsule consists of
collagen fibers tissues that
appear under the
microscope as wavy lines
(see figure)
However, the capsule line is sometimes unrecognizable because of the
naturally occurring intrusion of muscle into the prostate gland which
makes the segmentation problem more challenging.

38. 38
Summary
 Introduction
 Edge-based segmentation
 Region-based segmentation
– Region Growing
– Split-and-merge
 Active contour models (snakes)
 Application in medical imaging
 Conclusion

39. 39
Conclusion
 Edge detection and region growing algorithms are
very popular in most commercial image analysis
tools
 The reason is that they are simple to understand
and to implement, and they are very generic, as
they do not assume specific knowledge about the
objects to be analyzed.
 These methods are often the starting point for more
sophisticated model-based methods

40. 40
Conclusion
 For complex image data, such as medical images,
their usefulness is quite limited.
 Effective image analysis methods must incorporate
a priori knowledge of the considered structures
such as photometric properties (object intensity,
contrast, texture); geometric properties (position,
shape, motion, deformation); and the context, such
as the relative position with respect to the other
objects in the neighborhood