Downloaded 199 times
Uploaded byJyoti Dhall
Edge detection
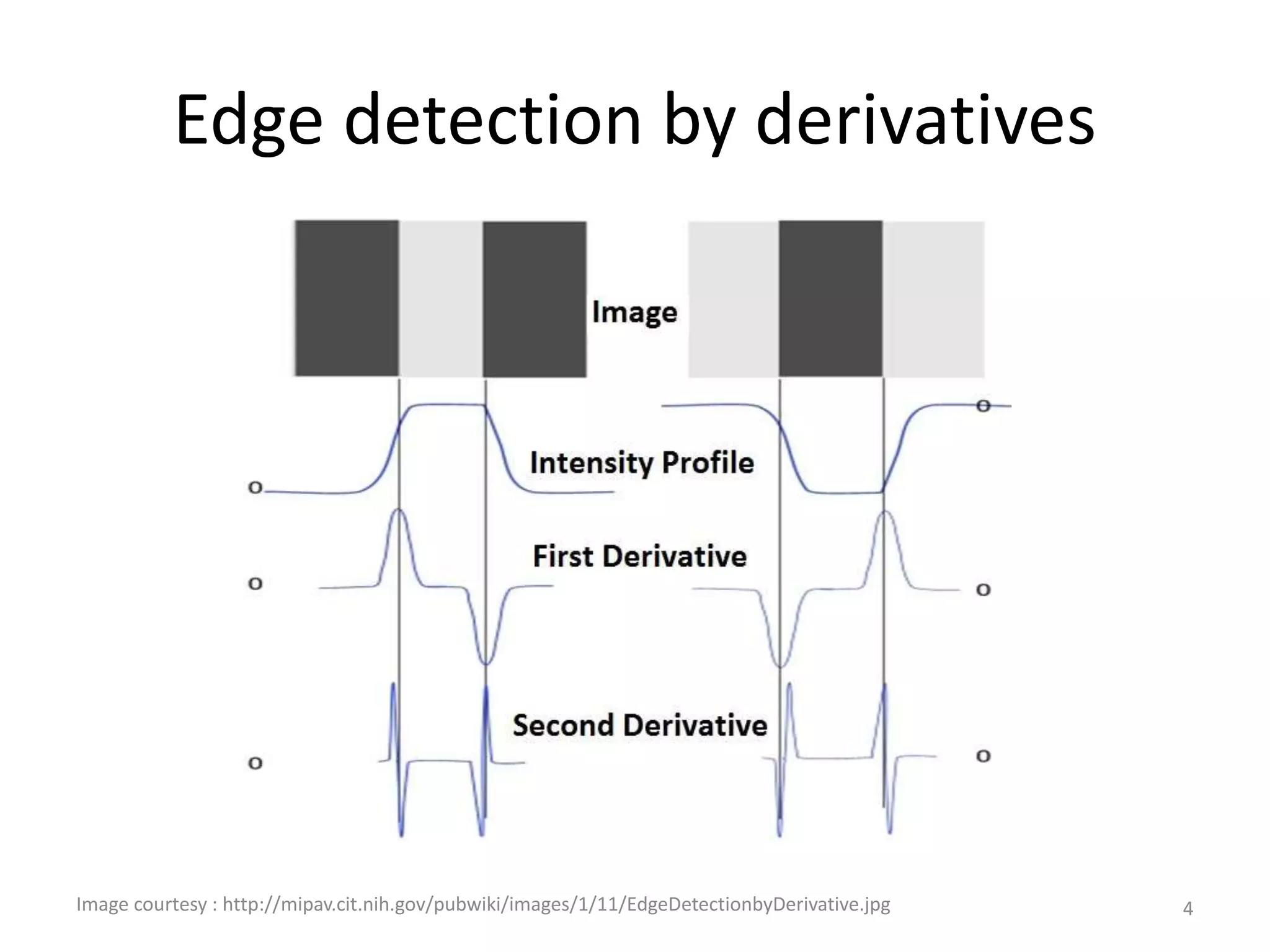
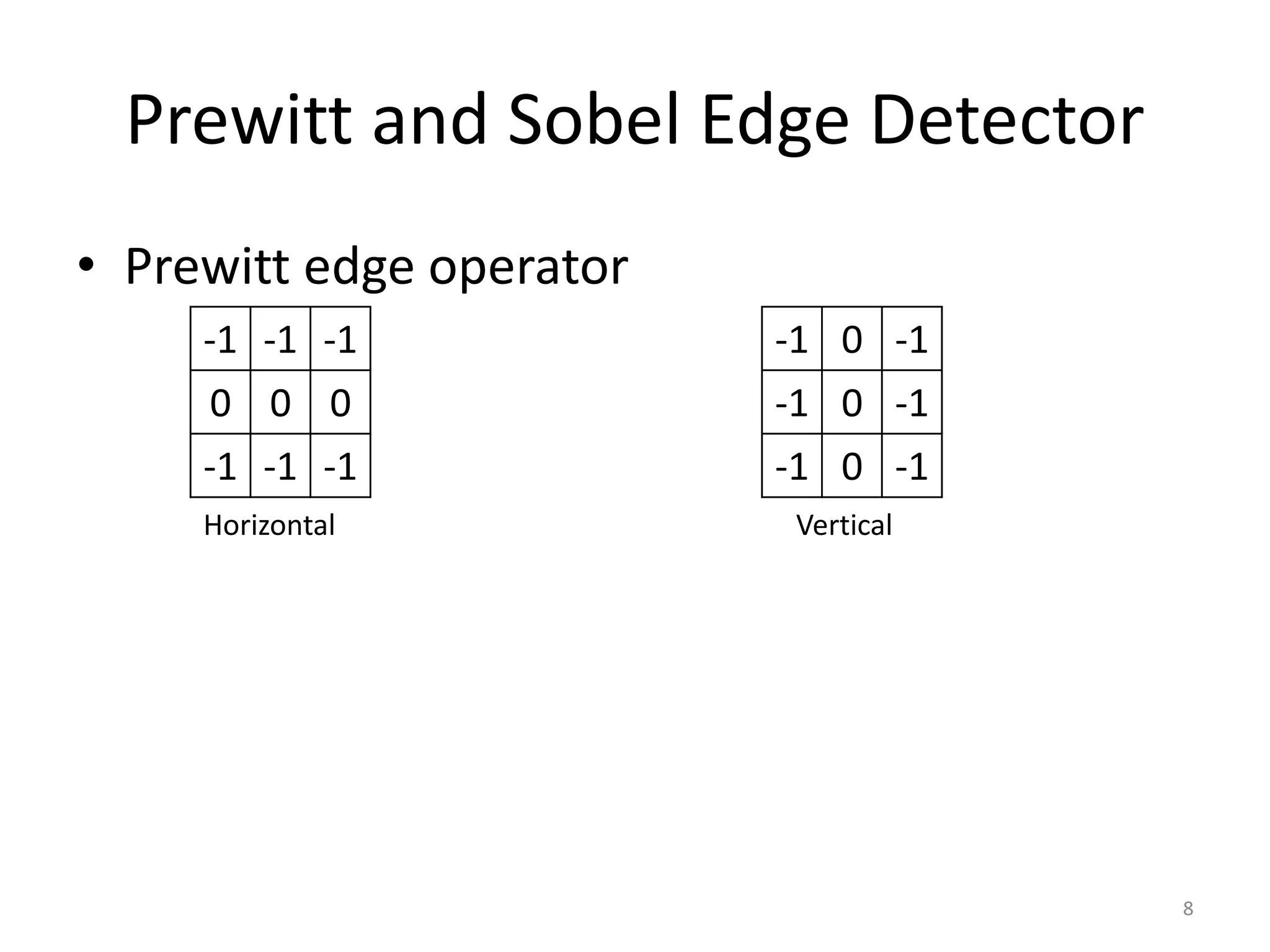
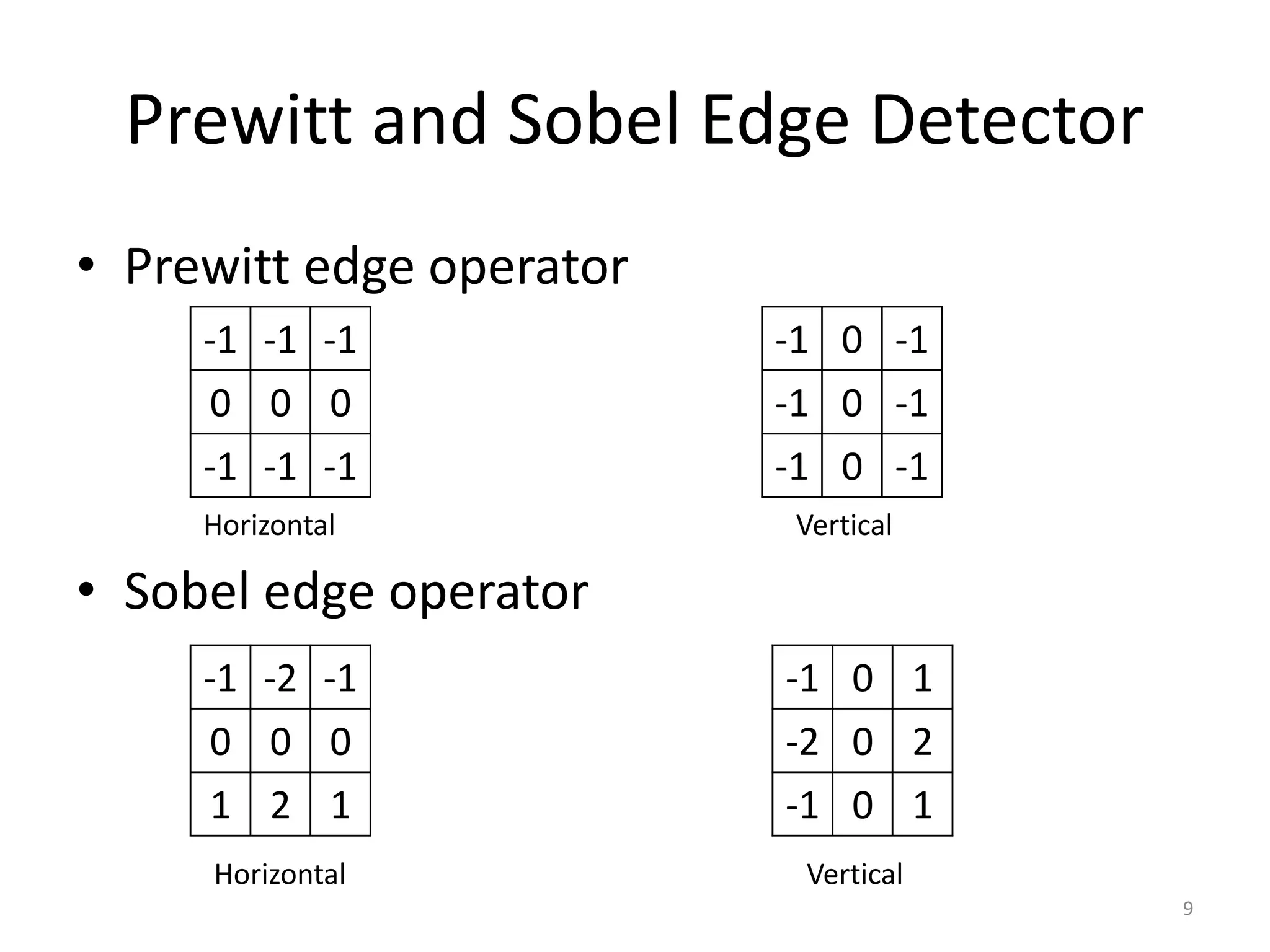
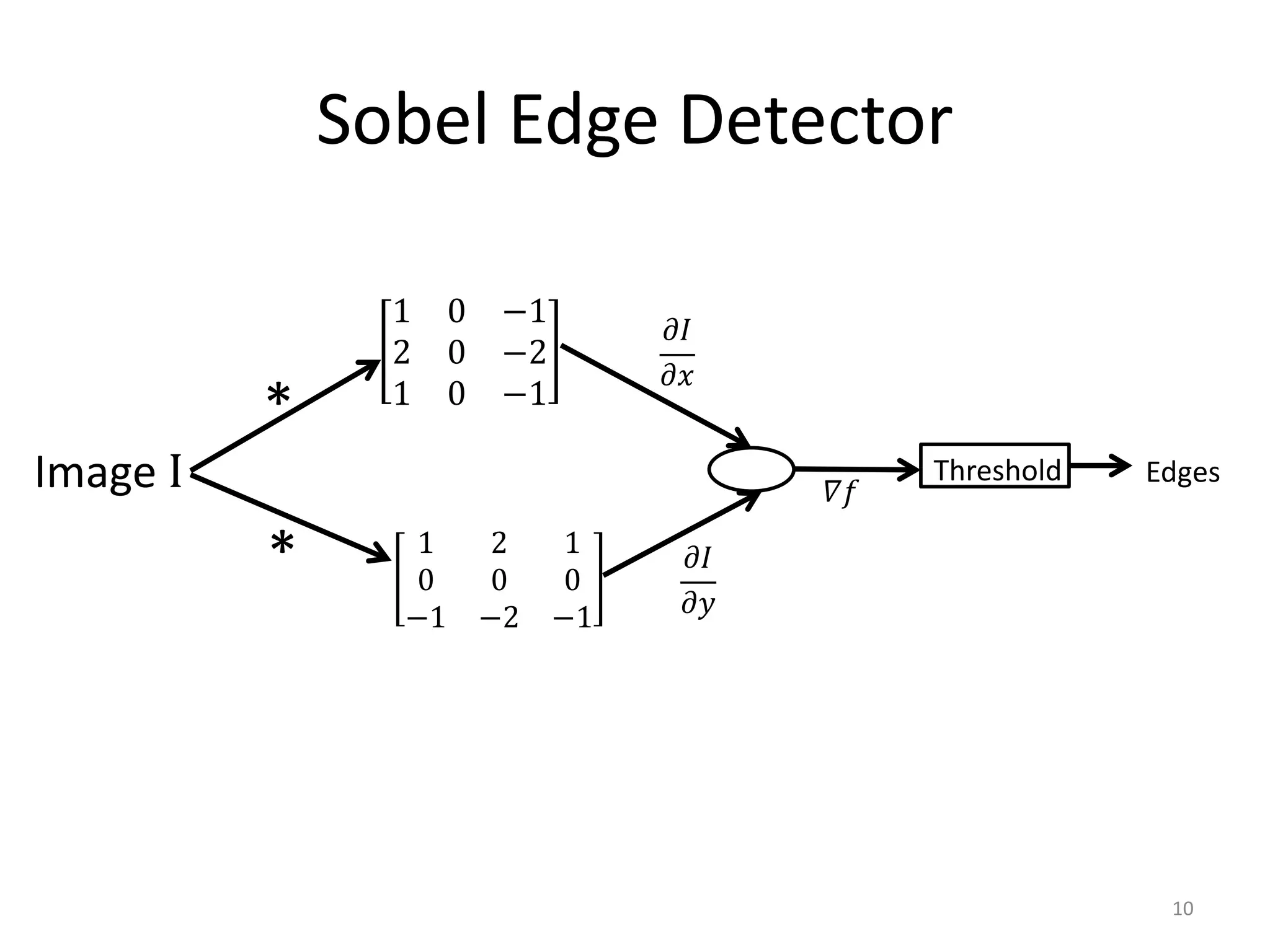
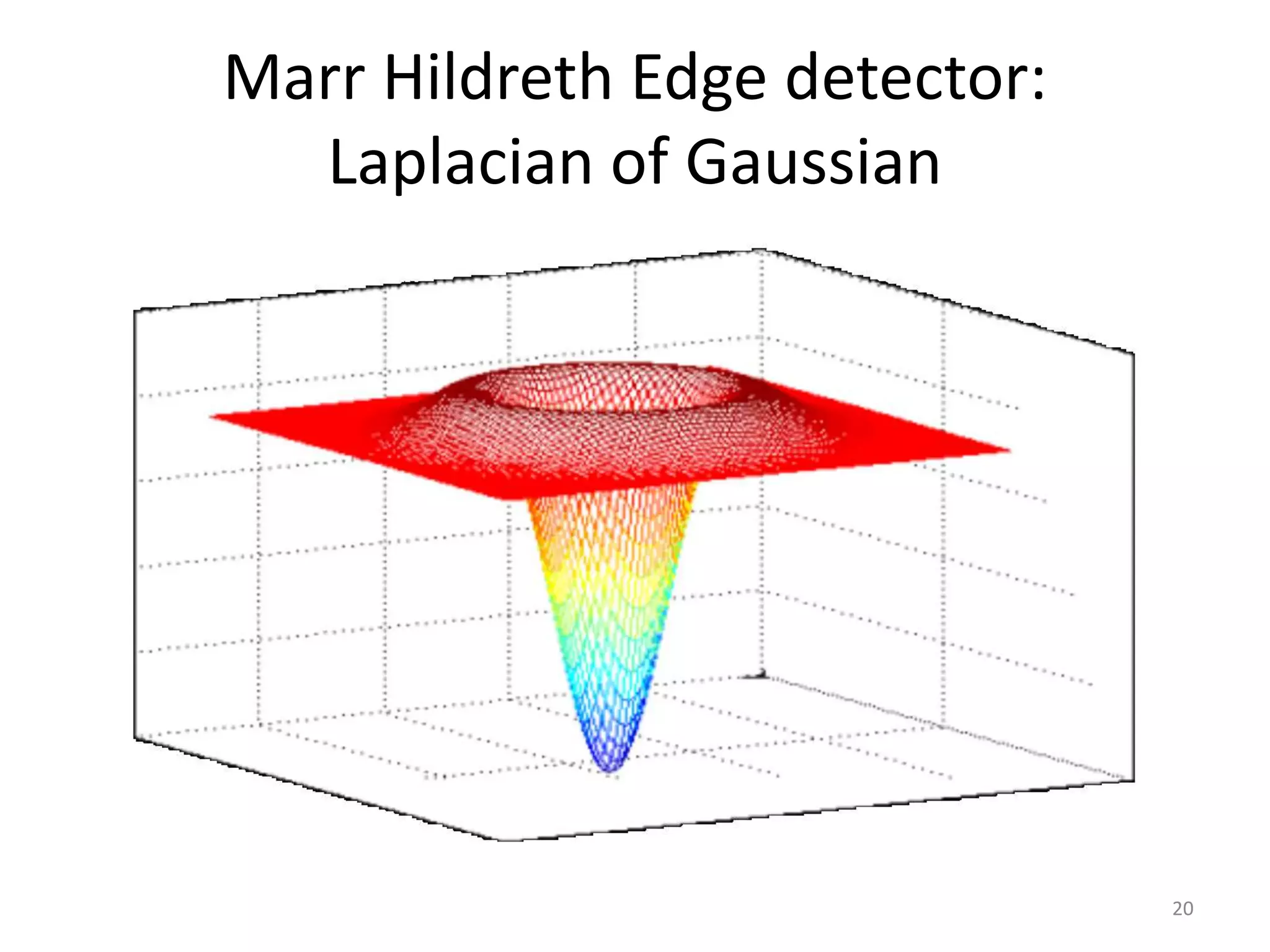
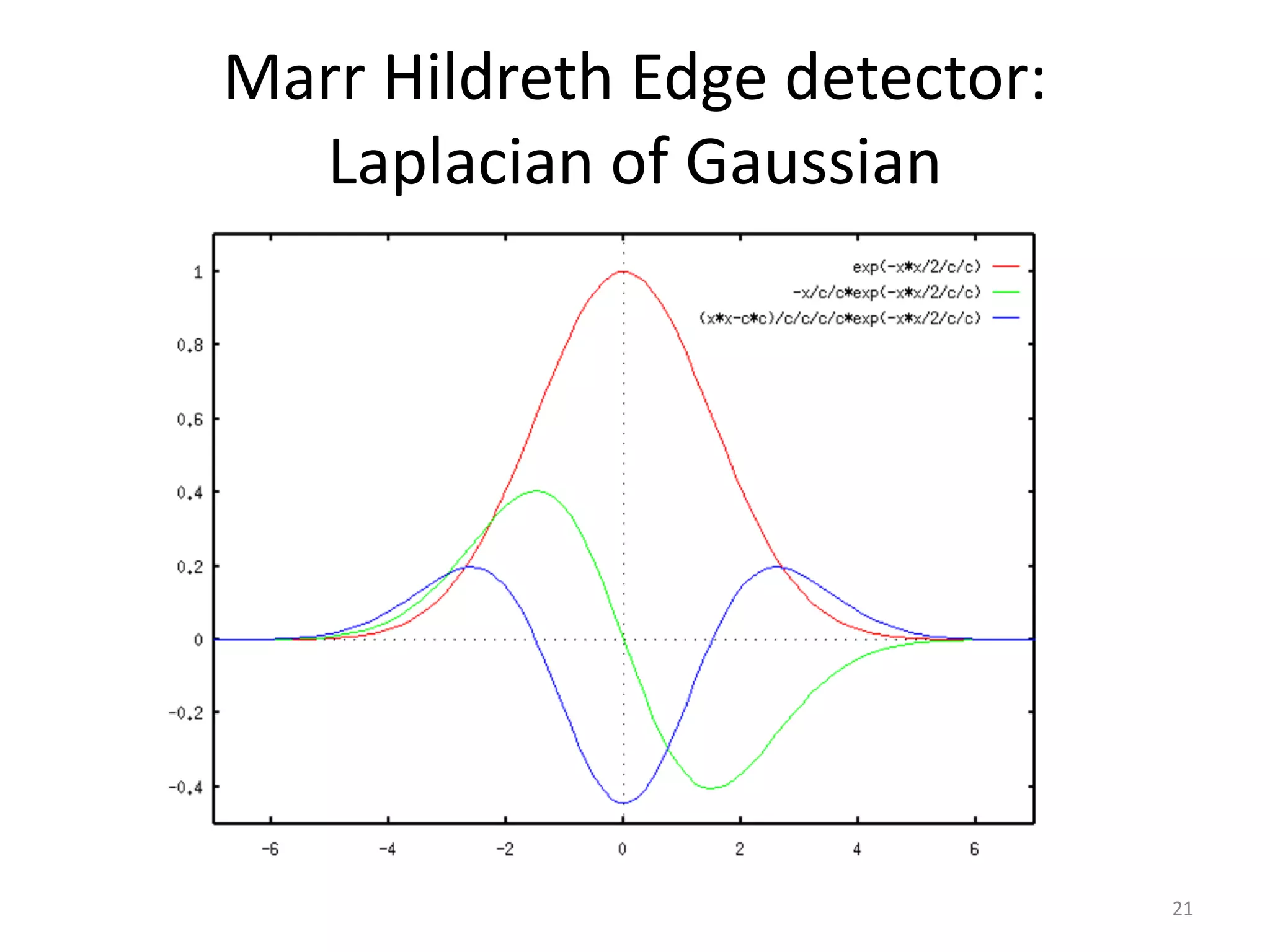
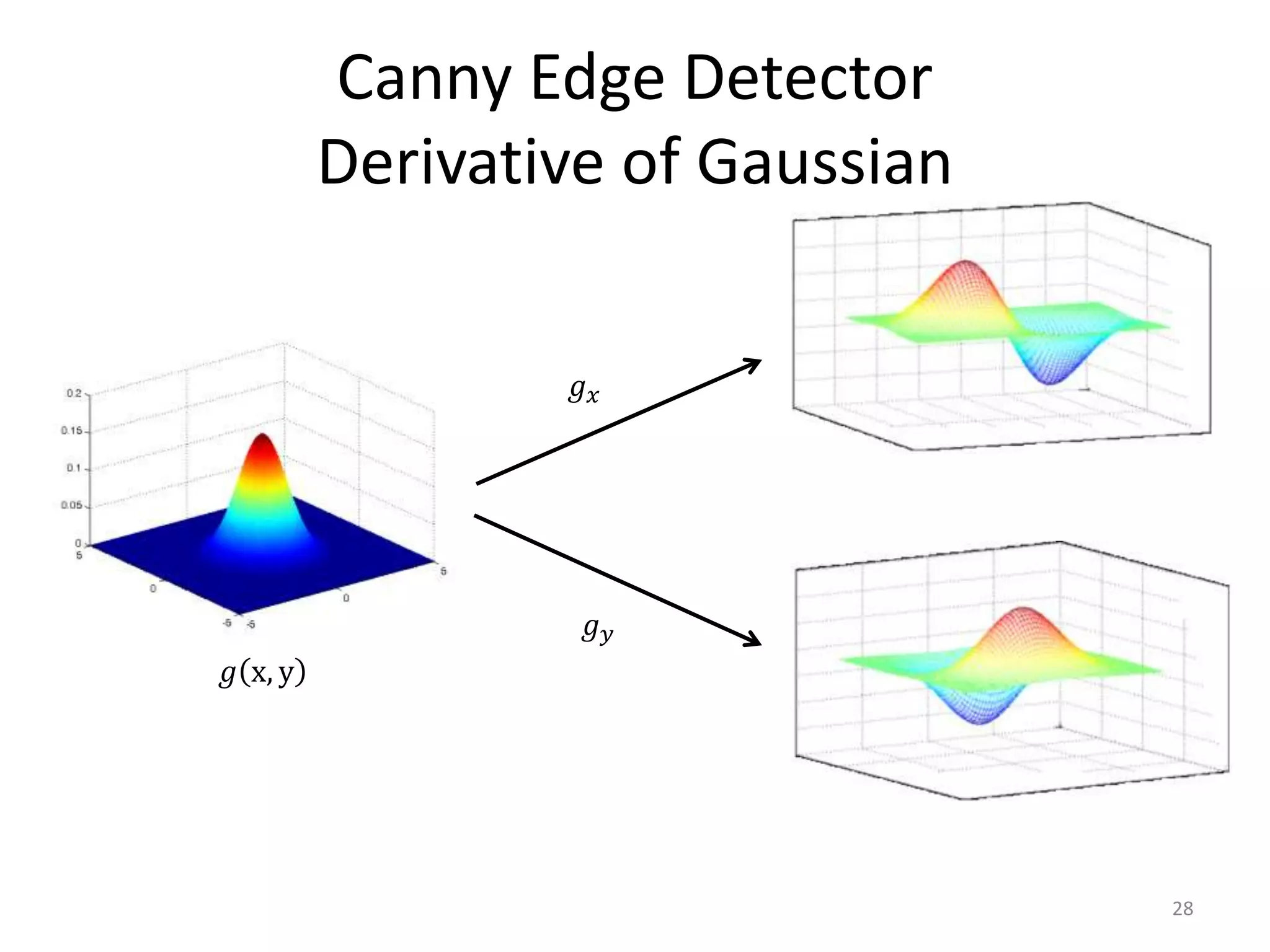
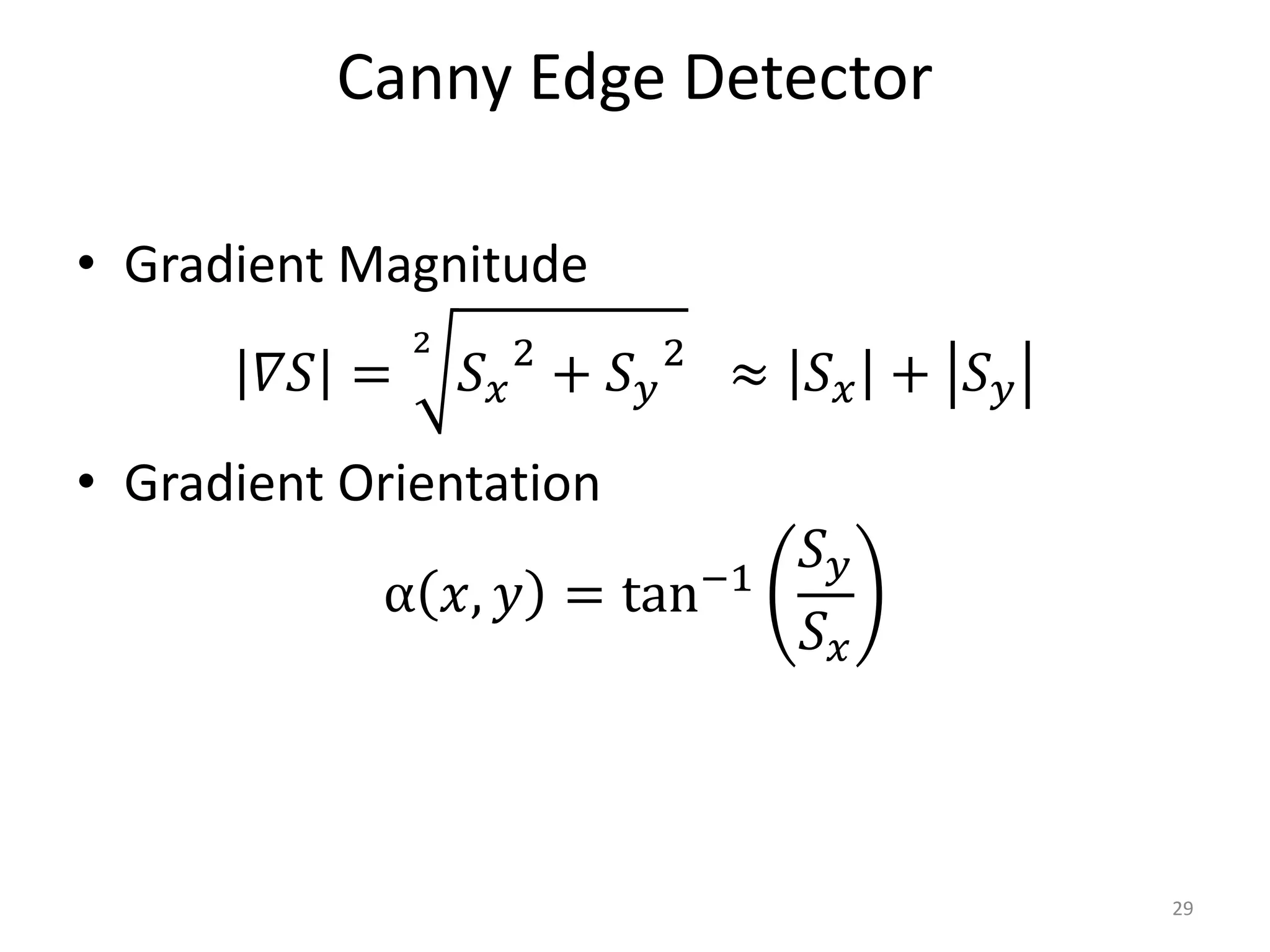
Edge detection algorithms identify points in a digital image where the image brightness changes sharply or has discontinuities. Common edge detection methods include gradient operators like Prewitt and Sobel, the Laplacian of Gaussian (LoG) used in Marr-Hildreth edge detection, and the Canny edge detector. The Canny edge detector applies smoothing, finds the image gradient, performs non-maximum suppression and double thresholding to detect edges with good localization and a single response to each edge.
More Related Content
![Vibe Coding vs. Spec-Driven Development [Free Meetup]](https://cdn.slidesharecdn.com/ss_thumbnails/vibecodingvsspecdrivendevelopment-251209105622-43f455e7-thumbnail.jpg?width=640&height=640&fit=bounds)
Edge detection
- 1. Edge Detection • EdgeDetection – Identifying sudden change in image intensity. • Applications – Various machine vision problems such as Object Segmentation, Scene understanding etc. 1
- 2. What is anedge? • Discontinuity of intensities in the image • Types of Edges 2
- 3. Edge Detectors • GradientOperators – Prewitt – Sobel • Laplacian of Gaussian (Marr-Hildreth) • Gradient of Gaussian (Canny) 3
- 4. Edge detection byderivatives 4Image courtesy : http://mipav.cit.nih.gov/pubwiki/images/1/11/EdgeDetectionbyDerivative.jpg
- 5. Edge detection byfirst derivative • I = 𝑓 𝑥, 𝑦 • 𝛻𝑓 = 𝐺 𝑥 𝐺 𝑦 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 • 𝛻𝑓 = 𝑚𝑎𝑔 𝛻𝑓 = 2 𝐺 𝑥 2 + 𝐺 𝑦 2 ≈ 𝐺 𝑥 + 𝐺 𝑦 • Direction of 𝛻𝑓, α 𝑥, 𝑦 = tan−1 𝐺 𝑦 𝐺 𝑥 5
- 6. Edge detection byfirst derivative • I = 𝑓 𝑥, 𝑦 • 𝛻𝑓 = 𝐺 𝑥 𝐺 𝑦 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 • 𝛻𝑓 = 𝑚𝑎𝑔 𝛻𝑓 = 2 𝐺 𝑥 2 + 𝐺 𝑦 2 ≈ 𝐺 𝑥 + 𝐺 𝑦 • Direction of 𝛻𝑓, α 𝑥, 𝑦 = tan−1 𝐺 𝑦 𝐺 𝑥 6
- 7. • Prewitt edgeoperator Prewitt and Sobel Edge Detector -1 -1 -1 0 0 0 -1 -1 -1 8 -1 0 -1 -1 0 -1 -1 0 -1 Horizontal Vertical
- 8. • Prewitt edgeoperator • Sobel edge operator Prewitt and Sobel Edge Detector -1 -1 -1 0 0 0 -1 -1 -1 9 -1 0 -1 -1 0 -1 -1 0 -1 Horizontal Vertical -1 -2 -1 0 0 0 1 2 1 -1 0 1 -2 0 2 -1 0 1 Horizontal Vertical
- 9. 1 0 −1 20 −2 1 0 −1 1 2 1 0 0 0 −1 −2 −1 Sobel Edge Detector 10 Image I * * 𝜕𝐼 𝜕𝑥 𝜕𝐼 𝜕𝑦 𝛻𝑓 Threshold Edges
- 10.
- 11. Marr Hildreth Edgedetector • Laplacian of Gaussian • Smooth image by Gaussian filter • Apply Laplacian to smoothed image • Find zero crossing – Scan along each row, record an edge point at the location of zero crossing – Repeat the step along each column 12
- 12. • Gaussian Smoothing 𝑆𝑚𝑜𝑜𝑡ℎ𝑒𝑑𝐼𝑚𝑎𝑔𝑒 𝐺𝑎𝑢𝑠𝑠𝑖𝑎𝑛 𝑓𝑖𝑙𝑡𝑒𝑟 𝐼𝑚𝑎𝑔𝑒 𝑆 = 𝑔 ∗ 𝐼 Marr Hildreth Edge detector 13
- 13. • Gaussian Smoothing 𝑆𝑚𝑜𝑜𝑡ℎ𝑒𝑑𝐼𝑚𝑎𝑔𝑒 𝐺𝑎𝑢𝑠𝑠𝑖𝑎𝑛 𝑓𝑖𝑙𝑡𝑒𝑟 𝐼𝑚𝑎𝑔𝑒 𝑆 = 𝑔 ∗ 𝐼 𝑔 = 𝑔 𝑥, 𝑦 = 1 𝜎 2𝜋 𝑒 − 𝑥2+𝑦2 2𝜎2 where 𝜎 𝑖𝑠 𝑆𝐷 Marr Hildreth Edge detector 14
- 14. • Gaussian Smoothing 𝑆𝑚𝑜𝑜𝑡ℎ𝑒𝑑𝐼𝑚𝑎𝑔𝑒 𝐺𝑎𝑢𝑠𝑠𝑖𝑎𝑛 𝑓𝑖𝑙𝑡𝑒𝑟 𝐼𝑚𝑎𝑔𝑒 𝑆 = 𝑔 ∗ 𝐼 𝑔 = 𝑔 𝑥, 𝑦 = 1 𝜎 2𝜋 𝑒 − 𝑥2+𝑦2 2𝜎2 where 𝜎 𝑖𝑠 𝑆𝐷 Marr Hildreth Edge detector 15
- 15. Marr Hildreth Edgedetector • Laplacian operator 𝛻2 𝑓 = 𝜕2 𝑓 𝜕𝑥2 + 𝜕2 𝑓 𝜕𝑦2 16
- 16. Marr Hildreth Edgedetector • Laplacian operator 𝛻2 𝑓 = 𝜕2 𝑓 𝜕𝑥2 + 𝜕2 𝑓 𝜕𝑦2 • Laplacian of Gaussian (LoG) 𝛻2 𝑆 = 𝛻2 𝑔 ∗ 𝐼 = (𝛻2 𝑔) ∗ 𝐼 17
- 17. Marr Hildreth Edgedetector • Laplacian operator 𝛻2 𝑓 = 𝜕2 𝑓 𝜕𝑥2 + 𝜕2 𝑓 𝜕𝑦2 • Laplacian of Gaussian (LoG) 𝛻2 𝑆 = 𝛻2 𝑔 ∗ 𝐼 = (𝛻2 𝑔) ∗ 𝐼 𝛻2 𝑔 = − 1 2𝜋𝜎3 2 − 𝑥2+𝑦2 𝜎2 𝑒 − 𝑥2+𝑦2 2𝜎2 18
- 18. Marr Hildreth Edgedetector: Laplacian of Gaussian 20
- 19. Marr Hildreth Edgedetector: Laplacian of Gaussian 21
- 20. 22 Marr Hildreth Edgedetector Example
- 21. Canny Edge Detector •Three main criteria – Good Detection : The ability to locate and mark all real edges – Good Localisation : Minimal distance between the detected edge and real edge – Clear Response : Only one response per edge 23
- 22. Canny Edge Detector •Image Smoothing with Gaussian filter • Compute derivative of smoothed image • Find magnitude and orientation of gradient • Apply ‘Non-maximum Suppression’ • Apply Threshold 24
- 23. Canny Edge Detector •Smoothing 𝑆 = 𝐼 ∗ 𝑔 = 𝑔 x, y ∗ 𝐼 𝑔 𝑥, 𝑦 = 1 𝜎 2𝜋 𝑒 − 𝑥2+𝑦2 2𝜎2 25
- 24. Canny Edge Detector •Smoothing 𝑆 = 𝐼 ∗ 𝑔 = 𝑔 x, y ∗ 𝐼 𝑔 𝑥, 𝑦 = 1 𝜎 2𝜋 𝑒 − 𝑥2+𝑦2 2𝜎2 • Derivative 𝛻𝑆 = 𝛻 𝑔 ∗ 𝐼 = 𝛻𝑔 ∗ 𝐼 𝛻𝑔 = 𝜕𝑔 𝜕𝑥 𝜕𝑔 𝜕𝑦 = 𝑔 𝑥 𝑔 𝑦 26
- 25. Canny Edge Detector •Smoothing 𝑆 = 𝐼 ∗ 𝑔 = 𝑔 x, y ∗ 𝐼 𝑔 𝑥, 𝑦 = 1 𝜎 2𝜋 𝑒 − 𝑥2+𝑦2 2𝜎2 • Derivative 𝛻𝑆 = 𝛻 𝑔 ∗ 𝐼 = 𝛻𝑔 ∗ 𝐼 𝛻𝑔 = 𝜕𝑔 𝜕𝑥 𝜕𝑔 𝜕𝑦 = 𝑔 𝑥 𝑔 𝑦 𝛻𝑆 = 𝑔 𝑥 𝑔 𝑦 ∗ 𝐼 = 𝑔 𝑥 ∗ 𝐼 𝑔 𝑦 ∗ 𝐼 27
- 26. Canny Edge Detector Derivativeof Gaussian 28 𝑔 x, y 𝑔 𝑥 𝑔 𝑦
- 27. Canny Edge Detector •Gradient Magnitude 𝛻𝑆 = 2 𝑆 𝑥 2 + 𝑆 𝑦 2 ≈ 𝑆 𝑥 + 𝑆 𝑦 • Gradient Orientation α 𝑥, 𝑦 = tan−1 𝑆 𝑦 𝑆 𝑥 29
- 28. Canny Edge Detector Nonmaximum Suppression 30 Image Courtesy: https://teroninsights.wordpress.com/ • Suppress the pixels in 𝛻𝑆 which are not local maximum • 𝑀 𝑥, 𝑦 = 𝛻𝑆 𝑖, 𝑗 𝑖𝑓 𝛻𝑆 𝑖, 𝑗 > 𝛻𝑆 (𝑖 − 1, 𝑗 + 1) 𝑎𝑛𝑑 𝛻𝑆 𝑖, 𝑗 > 𝛻𝑆 (𝑖 + 1, 𝑗 − 1) 0 𝑂𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
- 29. Canny Edge Detector HysteresisThresholding • If the gradient at the pixel is – Above ‘High’, declare it as an ‘edge pixel’ – Below ‘Low’, declare it as a ‘non-edge pixel’ – Between ‘Low’ and ‘High’ • Consider its neighbours iteratively then declare it as an edge pixel, if it is connected to an edge pixel directly or via pixels between low and high 31
- 30.