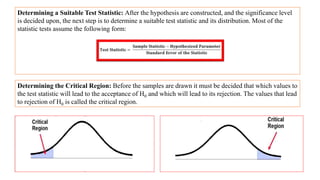
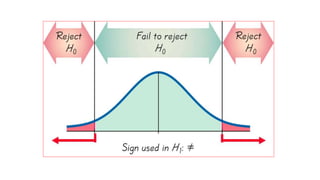
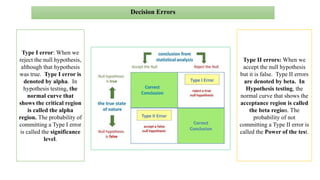
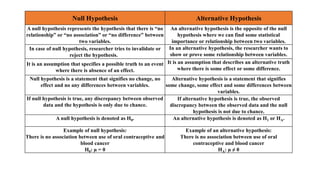
The document discusses hypothesis testing, which involves testing a hypothesis about a population using a sample of data. It explains that a hypothesis test has four main steps: 1) stating the null and alternative hypotheses, where the null hypothesis asserts there is no difference between the sample and population, 2) setting the significance level, 3) determining the test statistic and critical region for rejecting the null hypothesis, and 4) making a decision to reject or fail to reject the null hypothesis based on whether the test statistic falls in the critical region. Type I and type II errors are also defined. The document provides examples of null and alternative hypotheses using mathematical symbols and discusses how to determine if a p-value is statistically significant.

1. The Hypothesis is an assumption which is tested to check whether the inference drawn
from the sample of data stand true for the entire population or not.

2. Introduction
A Hypothesis test is a statistical test that is used to determine whether there is
enough evidence in a sample of data to infer that a certain condition is true for the
entire population.
If you believe something might be true but don’t yet have definitive proof, it is
considered a theory until that proof is provided. It consists of 4 steps:

4. The Null Hypothesis
The Null Hypothesis denoted by H0 asserts
that there is no true difference between the
sample of data and the population
parameter and that the difference is
accidental which is caused due to the
fluctuations in sampling.
Thus, a null hypothesis states that there is
no difference between the assumed and
actual value of the parameter.
The null hypothesis states that a population
parameter is equal to a value. The null
hypothesis is often an initial claim that
researchers specify using previous research
or knowledge.
The Alternate Hypothesis
The alternative hypothesis denoted by H1
or HA is the other hypothesis about the
population, which stands true if the null
hypothesis is rejected. Contrary to the
null hypothesis, the alternative hypothesis
shows that observations are the result of a
real effect.
It states that sample observations are
influenced by some non-random cause.
The alternative hypothesis states that the
population parameter is different than the
value of the population parameter in the
null hypothesis. The alternative
hypothesis is what you might believe to
be true or hope to prove true.
For Example
When your car breakdown you will make an educated guess that there may be not enough petrol or may be
some technical problem. Then you will take car to the nearest workshop to validate your
guess/assumption/hypothesis. Depend on Mechanic answer you will reject one hypothesis and accept
another hypothesis.
Here Null hypothesis is “not enough petrol”; Alternate hypothesis is may be some technical problem.

5. For example, suppose we wanted to determine whether a coin was fair and balanced. A null hypothesis might be that half
the flips would result in Heads and half, in Tails. The alternative hypothesis might be that the number of Heads and Tails
would be very different. Symbolically, these hypotheses would be expressed as
Ho: P = 0.5
Ha: P ≠ 0.5
Suppose we flipped the coin 50 times, resulting in 40 Heads and 10 Tails. Given this result, we would be inclined to reject
the null hypothesis. We would conclude, based on the evidence, that the coin was probably not fair and balanced.
Can We Accept the Null Hypothesis?
Some researchers say that a hypothesis test can have one of two outcomes: you accept the null hypothesis or you reject
the null hypothesis. Many statisticians, however, take issue with the notion of "accepting the null hypothesis." Instead,
they say: you reject the null hypothesis or you are failed to reject the null hypothesis.
Why the distinction between "acceptance" and "failure to reject?" Acceptance implies that the null hypothesis is
true. Failure to reject implies that the data are not sufficiently persuasive for us to prefer the alternative hypothesis
over the null hypothesis.

6. Hypothesis: Using Math Symbols

7. Set up a Suitable Significance Levels
Once the hypothesis about the population is constructed the researcher has to decide the level of
significance, i.e. a confidence level with which the null hypothesis is accepted or rejected. The
significance level is denoted by ‘α’ and is usually defined before the samples are drawn such that
results obtained do not influence the choice.
In practice, we either take 5% or 1% level of significance.
If the 5% level of significance is taken, it means that there are five chances out of 100 that we will
reject the null hypothesis when it should have been accepted, i.e. we are about 95% confident that
we have made the right decision.
Similarly, if the 1% level of significance is taken, it means that there is only one chance out of 100
that we reject the hypothesis when it should have been accepted, and we are about 99% confident
that the decision made is correct.

8. Determining a Suitable Test Statistic: After the hypothesis are constructed, and the significance level
is decided upon, the next step is to determine a suitable test statistic and its distribution. Most of the
statistic tests assume the following form:
Determining the Critical Region: Before the samples are drawn it must be decided that which values to
the test statistic will lead to the acceptance of H0 and which will lead to its rejection. The values that lead
to rejection of H0 is called the critical region.

10. Decision Errors
Type I error: When we
reject the null hypothesis,
although that hypothesis
was true. Type I error is
denoted by alpha. In
hypothesis testing, the
normal curve that
shows the critical region
is called the alpha
region. The probability of
committing a Type I error
is called the significance
level.
Type II errors: When we
accept the null hypothesis
but it is false. Type II errors
are denoted by beta. In
Hypothesis testing, the
normal curve that shows the
acceptance region is called
the beta region. The
probability of not
committing a Type II error is
called the Power of the test.

11. Decision Rules
• P-value: The strength of evidence in support of a null hypothesis is measured by the P-value.
Suppose the test statistic is equal to S. The P-value is the probability of observing a test statistic as
extreme as S, assuming the null hypothesis is true. If the P-value is less than the significance level,
we reject the null hypothesis.
• Region of acceptance: The region of acceptance is a range of values. If the test statistic falls
within the region of acceptance, the null hypothesis is not rejected. The region of acceptance is
defined so that the chance of making a Type I error is equal to the significance level.
• The set of values outside the region of acceptance is called the region of rejection. If the test
statistic falls within the region of rejection, the null hypothesis is rejected. In such cases, we say
that the hypothesis has been rejected at the α level of significance.

13. How do you know if a p-value is statistically significant?
The level of statistical significance is often expressed as a p-value between 0 and 1. The smaller
the p-value, the stronger the evidence that you should reject the null hypothesis.
A p-value less than 0.05 (typically ≤ 0.05) is statistically significant. It indicates strong evidence
against the null hypothesis, as there is less than a 5% probability the null is correct (and the results
are random). Therefore, we reject the null hypothesis, and accept the alternative hypothesis.
A p-value higher than 0.05 (> 0.05) is not statistically significant and indicates strong evidence
for the null hypothesis. This means we retain the null hypothesis and reject the alternative
hypothesis. You should note that you cannot accept the null hypothesis, we can only reject the null
or fail to reject it.
A statistically significant result cannot prove that a research hypothesis is correct (as this implies
100% certainty).
Instead, we may state our results “provide support for” or “give evidence for” our research
hypothesis (as there is still a slight probability that the results occurred by chance and the null
hypothesis was correct – e.g. less than 5%).

14. Null Hypothesis Alternative Hypothesis
A null hypothesis represents the hypothesis that there is “no
relationship” or “no association” or “no difference” between
two variables.
An alternative hypothesis is the opposite of the null
hypothesis where we can find some statistical
importance or relationship between two variables.
In case of null hypothesis, researcher tries to invalidate or
reject the hypothesis.
In an alternative hypothesis, the researcher wants to
show or prove some relationship between variables.
It is an assumption that specifies a possible truth to an event
where there is absence of an effect.
It is an assumption that describes an alternative truth
where there is some effect or some difference.
Null hypothesis is a statement that signifies no change, no
effect and no any differences between variables.
Alternative hypothesis is a statement that signifies
some change, some effect and some differences between
variables.
If null hypothesis is true, any discrepancy between observed
data and the hypothesis is only due to chance.
If alternative hypothesis is true, the observed
discrepancy between the observed data and the null
hypothesis is not due to chance.
A null hypothesis is denoted as H0. An alternative hypothesis is denoted as H1 or HA.
Example of null hypothesis:
There is no association between use of oral contraceptive and
blood cancer
H0: µ = 0
Example of an alternative hypothesis:
There is no association between use of oral
contraceptive and blood cancer
HA: µ ≠ 0