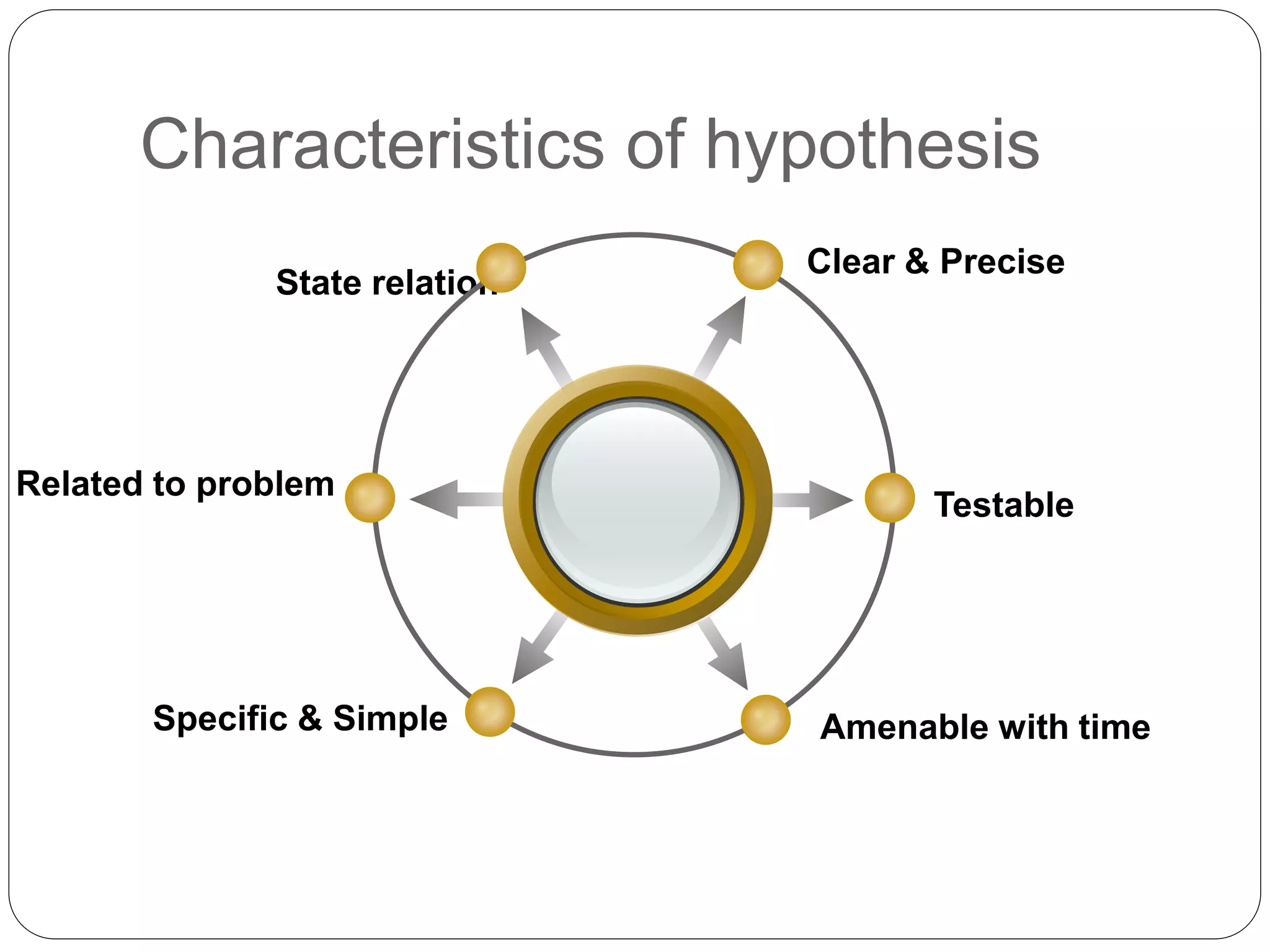
This document discusses key concepts related to testing hypotheses. It defines a hypothesis as a statement that can be tested scientifically to determine if it is true. The null hypothesis states that there is no effect or relationship, while the alternative hypothesis specifies what the test is designed to detect. Type I and Type II errors occur when the null hypothesis is incorrectly rejected or accepted. The level of significance refers to the probability of a Type I error. One-sided and two-sided tests determine whether the critical values are in one or both tails of the probability distribution. Finally, a decision rule establishes the criteria for rejecting or failing to reject the null hypothesis based on the sample results.

1. Test of
Hypothesis

2. Topics covered
Meaning of hypothesis
Characteristics of hypothesis
Basic concepts concerning testing of hypothesis
 Null and Alternative Hypothesis
 Type I and Type II errors
 Level of significance
 Decision rule or test of hypothesis

3. Test of Hypothesis
 Hypothesis- Hypothesis is generally considered
the most important instrument in research. Its
main function is to suggest new functions and
ideas.
 In social sciences where direct knowledge of
population parameters is rare ,hypothesis testing
is the often used for deciding whether sample
data supports our purpose or not.

4. Meaning of hypothesis
 In ordinary context:
 Hypothesis means mere assumptions or
supposition which are to be proved or disproved.
 In research context:
 Hypothesis is a formal question that is intended to
resolve.
“A research hypothesis is a predictive statement
capable of being tested by scientific methods that
relate an independent variable to some dependent
variable.”

5. For example,
Consider statements like the following ones:
 “Students who receive counseling will show a
greater increase in creativity than students not
receiving counseling”
 “the automobile A is performing as well as
automobile B.”
These are hypotheses capable of being
objectively verified and tested. Thus, we may
conclude that a hypothesis states what we are
looking for and it is a proposition which can be put
to a test to determine its validity.

6. Characteristics of hypothesis
State relation
Clear & Precise
Related to problem
Testable
Amenable with timeSpecific & Simple

7. Characteristics of a hypothesis
• Hypothesis should be able to relate to a
variable.
• Hypothesis should be clear and precise
• Hypothesis must be consistent with
most known facts
• Hypothesis should be capable of being
tested
• Hypothesis must be stated in very
simple terms.
• Hypothesis must be limited in scope

8. Basic concepts
concerning testing of
hypothesis

9. 1. Null Hypothesis and
Alternative hypothesis

10.  The null hypothesis is generally symbolized
as H0 and the alternative hypothesis as
Ha. Suppose we want to test the
hypothesis that the population mean is
equal to the hypothesized mean m(H0) =
100.
 Then we would say that the null hypothesis
is that the population mean is equal to the
hypothesized mean 100 and symbolically
we can express as:
H0: m =m (H0)=100

11.  The null hypothesis, H0 represents a
theory that has been put forward, either
because it is believed to be true or
because it is to be used as a basis for
argument, but has not been proved.
 For example, in a clinical trial of a new
drug, the null hypothesis might be that the
new drug is no better, on average, than the
current drug.
We would write
H0: there is no difference between the two
drugs on average.

12. Alternative hypothesis
• If our sample results do not support this
then we assume something else is true.
The alternative that we will accept is
known as alternative hypothesis Ha
• Alternative Hypothesis would be
• Ho: µ ≠ µHo i.e population mean is not
equal to hypothized mean

13. Alternative hypothesis
 The alternative hypothesis, Ha, is a
statement of what a statistical hypothesis
test is set up to establish
 For example, in a clinical trial of a new
drug, the alternative hypothesis might be
that the new drug has a different effect, on
average, compared to that of the current
drug.
We would write Ha: the two drugs have
different effects, on average..

14. Alternative hypothesis
 The alternative hypothesis might also be
that the new drug is better, on average,
than the current drug. In this case we
would write
Ha: the new drug is better than the current
drug, on average

15. Following considerations are kept
in view
 The alternative hypothesis is one which one
wants to prove
 We give special consideration to the null
hypothesis. This is due to the fact that the null
hypothesis relates to the statement being
tested, whereas the alternative hypothesis
relates to the statement to be accepted if the
null is rejected.
 The final conclusion once the test has been
carried out is always given in terms of the null
hypothesis. We either 'reject H0 in favour of
Ha' or 'do not reject H0'; we never conclude
'reject Ha', or even 'accept Ha'

16. Following considerations are kept
in view
 If we conclude 'do not reject H0', this does
not necessarily mean that the null
hypothesis is true, it only suggests that
there is no sufficient evidence against H0
in favour of Ha; rejecting the null
hypothesis then, suggests that the
alternative hypothesis may be true.

17. 2. Type I and type II errors in a
Hypothesis Yest

18. Type I Error
Type I error : In a hypothesis test, a type I error
occurs when the null hypothesis is rejected when
it is in fact true; that is, H0 is wrongly rejected.
For example
H0: there is no difference between the two drugs
on average.
 Type I error will occur if we conclude that the
two drugs produce different effects when actually
there isn’t a difference.

19.  A type I error is often considered to be
more serious, and therefore more
important to avoid, than a type II error. The
hypothesis test procedure is therefore
adjusted so that there is a guaranteed 'low'
probability of rejecting the null hypothesis
wrongly; this probability is never 0.

20. Type II Error
2. Type II error refers to the situation when we
accept the null hypothesis when it is false.
H0: there is no difference between the two drugs
on average.
Type II error will occur if we conclude that the two
drugs produce the same effect when actually
there is a difference.

21. Type I and Type II Errors – Example
 Your null hypothesis is that the battery for a heart
pacemaker has an average life of 300 days, with
the alternative hypothesis that the average life is
more than 300 days. You are the quality control
manager for the battery manufacturer.
(a)Would you rather make a Type I error or a Type II
error?
(b) Based on your answer to part (a), should you
use a high or low significance level?

22. Type I and Type II Errors –
Example
 Given H0 : average life of pacemaker = 300 days,
and HA: Average life of pacemaker > 300 days
(a)It is better to make a Type II error (where H0 is
false i.e average life is actually more than 300
days but we accept H0 and assume that the
average life is equal to 300 days)
(b)As we increase the significance level (α) we
increase the chances of making a type I error.
Since here it is better to make a type II error we
shall choose a low α.

23. 3. Level of significance
 This is a very important concept in the context of
hypothesis testing.
 The significance level of a statistical hypothesis
test is a fixed probability of wrongly rejecting the
null hypothesis H0, if it is in fact true.
 It is the probability of a type I error and is set by
the investigator in relation to the consequences of
such an error. That is, we want to make the
significance level as small as possible in order to
protect the null hypothesis and to prevent, as far
as possible, the investigator from inadvertently
making false claims.

24. Significance level
 The significance level is usually denoted by
Significance Level = P(type I error) = Usually,
the significance level is chosen to be = 0.05 =
5%.
• One-sided Test
• A one-sided test is a statistical hypothesis test
in which the values for which we can reject
the null hypothesis, H0 are located entirely in
one tail of the probability distribution.

25. Continued…
• In other words, the critical region for a
one-sided test is the set of values less
than the critical value of the test, or the
set of values greater than the critical
value of the test.
• A one-sided test is also referred to as a
one-tailed test of significance

26. Example
• Suppose we wanted to test a manufacturers
claim that there are, on average, 50 matches
in a box. We could set up the following
hypotheses
• Ho:µ =50 as against
• Ha: µ <50 or
• Ha:µ >50

27. Example
 Either of these two alternative
hypotheses would lead to a one-sided
test. Presumably, we would want to test
the null hypothesis against the first
alternative hypothesis since it would be
useful to know if there is likely to be less
than 50 matches, on average, in a box
(no one would complain if they get the
correct number of matches in a box or
more).

28. Continued…
• Yet another alternative hypothesis could
be tested against the same null, leading
this time to a two-sided test:
• Ho:µ =50 as against
• Ha: µ ≠ 50

29. Continued…
 That is, nothing specific can be said
about the average number of matches in
a box; only that, if we could reject the
null hypothesis in our test, we would
know that the average number of
matches in a box is likely to be less than
or greater than 50.

30. Two-Sided Test
 A two-sided test is a statistical
hypothesis test in which the values for
which we can reject the null hypothesis,
H0 are located in both tails of the
probability distribution.
 A two-sided test is also referred to as a
two-tailed test of significance.

31. 4.Decision rule or test of
hypothesis
Given a hypothesis H0 and an alternative hypothesis
Ha, we make a rule which is known as decision rule
according to which we accept H0 (i.e., reject Ha) or
reject H0 (i.e., accept Ha). For instance, if (H0 is that a
certain lot is good (there are very few defective items
in it) against Ha) that the lot is not good (there are too
many defective items in it), then we must decide the
number of items to be tested and the criterion for
accepting or rejecting the hypothesis. We might test 10
items in the lot and plan our decision saying that if
there are none or only 1 defective item among the 10,
we will accept H0 otherwise we will reject H0 (or accept
Ha). This sort of basis is known as decision rule.