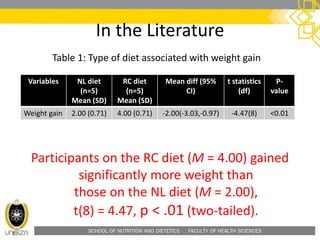
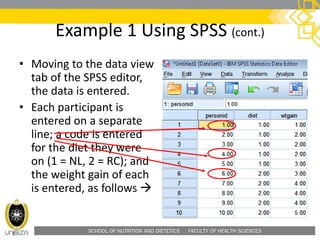
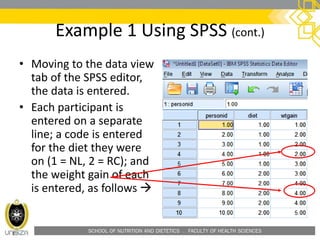
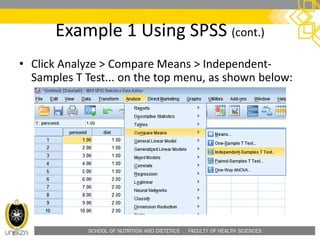
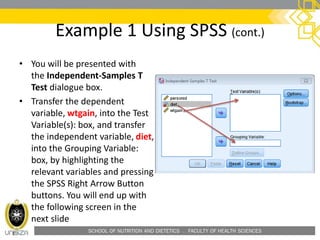
The document provides a comprehensive overview of the independent t-test, detailing its purpose to compare two independent groups and evaluate differences in means. It includes explanations of when to use the test, formulates the null and alternative hypotheses, and presents a practical example involving two different diets. The lecture also outlines the procedures for calculating the t-statistic and using statistical software (SPSS) for analysis.





![SCHOOL OF NUTRITION AND DIETETICS . FACULTY OF HEALTH SCIENCES
When to use the independent
samples t-test (cont.)
• Any differences between groups can be
explored with the independent t-test, as long
as the tested members of each group are
reasonably representative of the population.
[1]
[1] There are some technical
requirements as well. Principally,
each variable must come from a
normal (or nearly normal) distribution.](https://image.slidesharecdn.com/hfs3283independentt-test-160207015634/85/HFS-3283-independent-t-test-6-320.jpg)



























![SCHOOL OF NUTRITION AND DIETETICS . FACULTY OF HEALTH SCIENCES
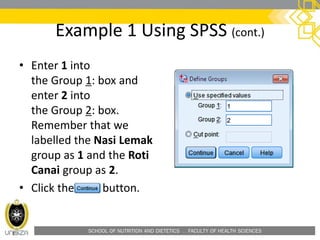
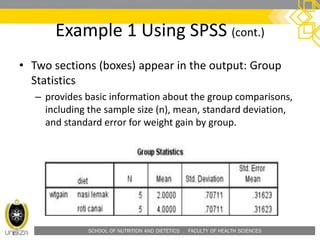
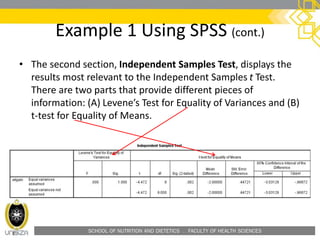
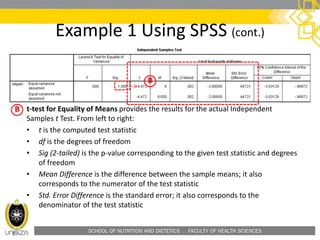
Example 1 Using SPSS (cont.)
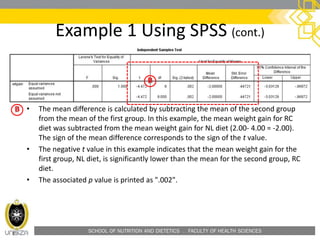
• Confidence Interval of the Difference: This part of the t-test output
complements the significance test results. Typically, if the CI for the mean
difference contains 0, the results are not significant at the chosen significance
level. In this example, the CI is [-3.03128, -0.96872], which does not contain
zero; this agrees with the small p-value of the significance test.](https://image.slidesharecdn.com/hfs3283independentt-test-160207015634/85/HFS-3283-independent-t-test-44-320.jpg)