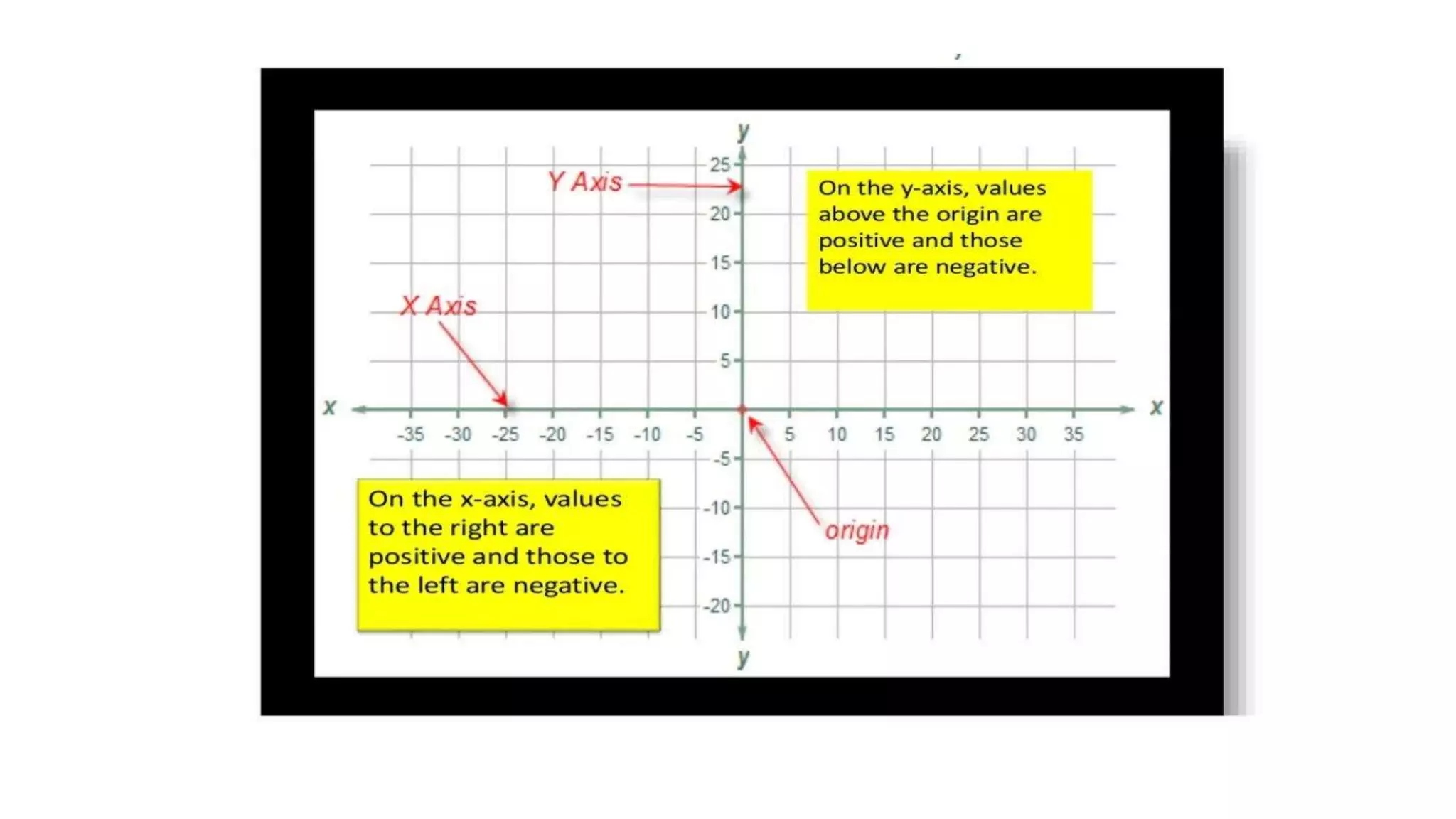
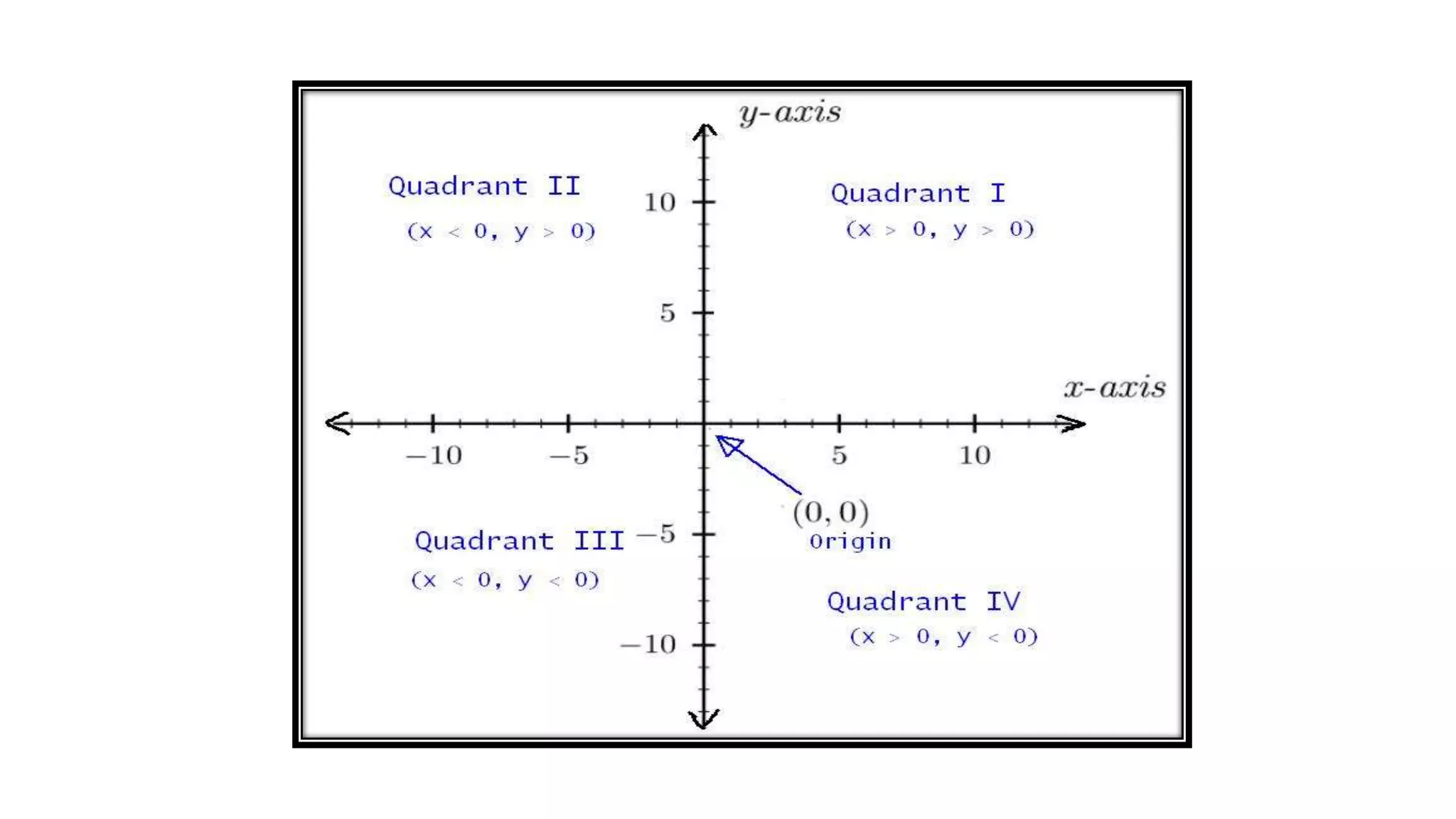
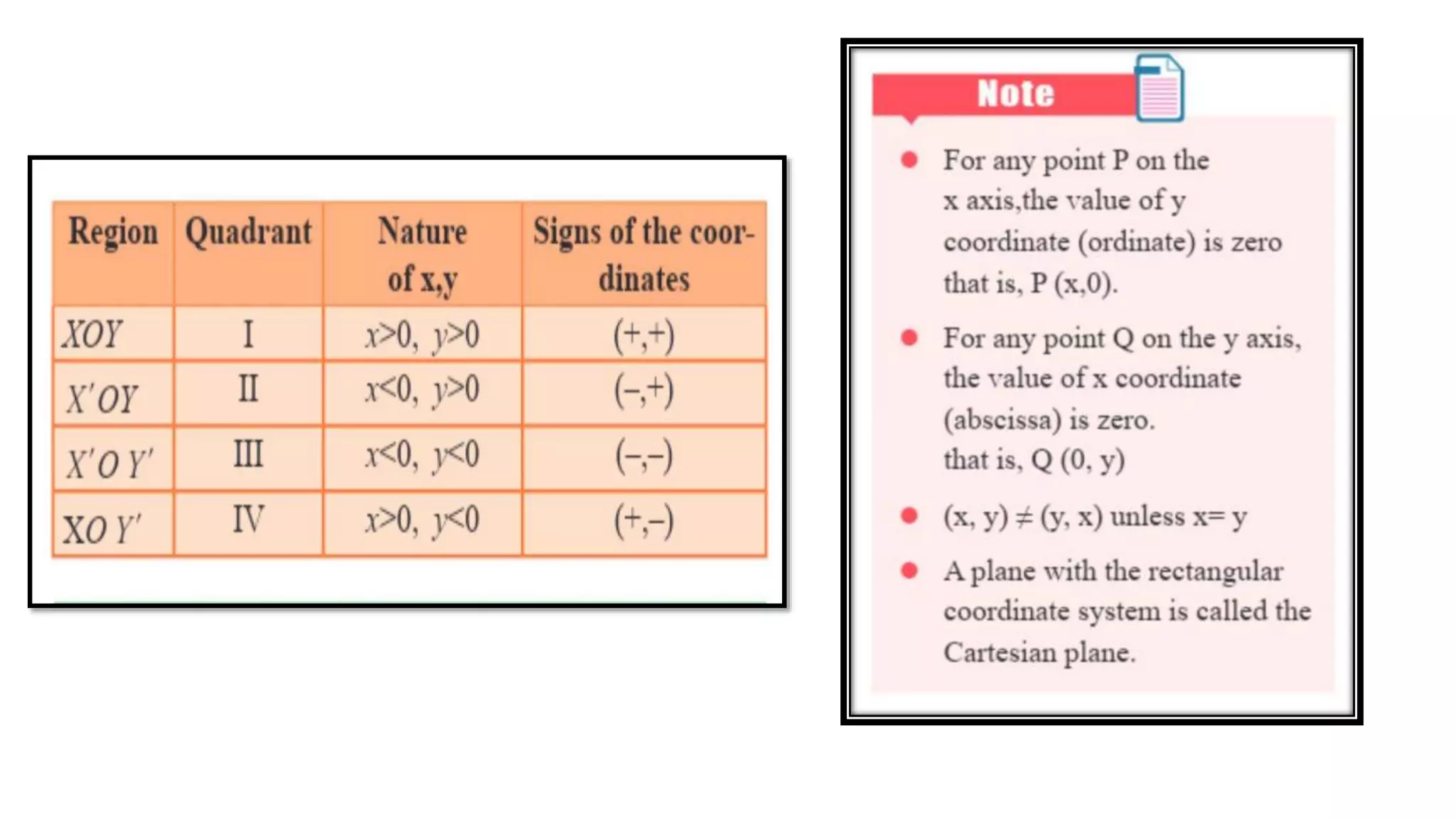
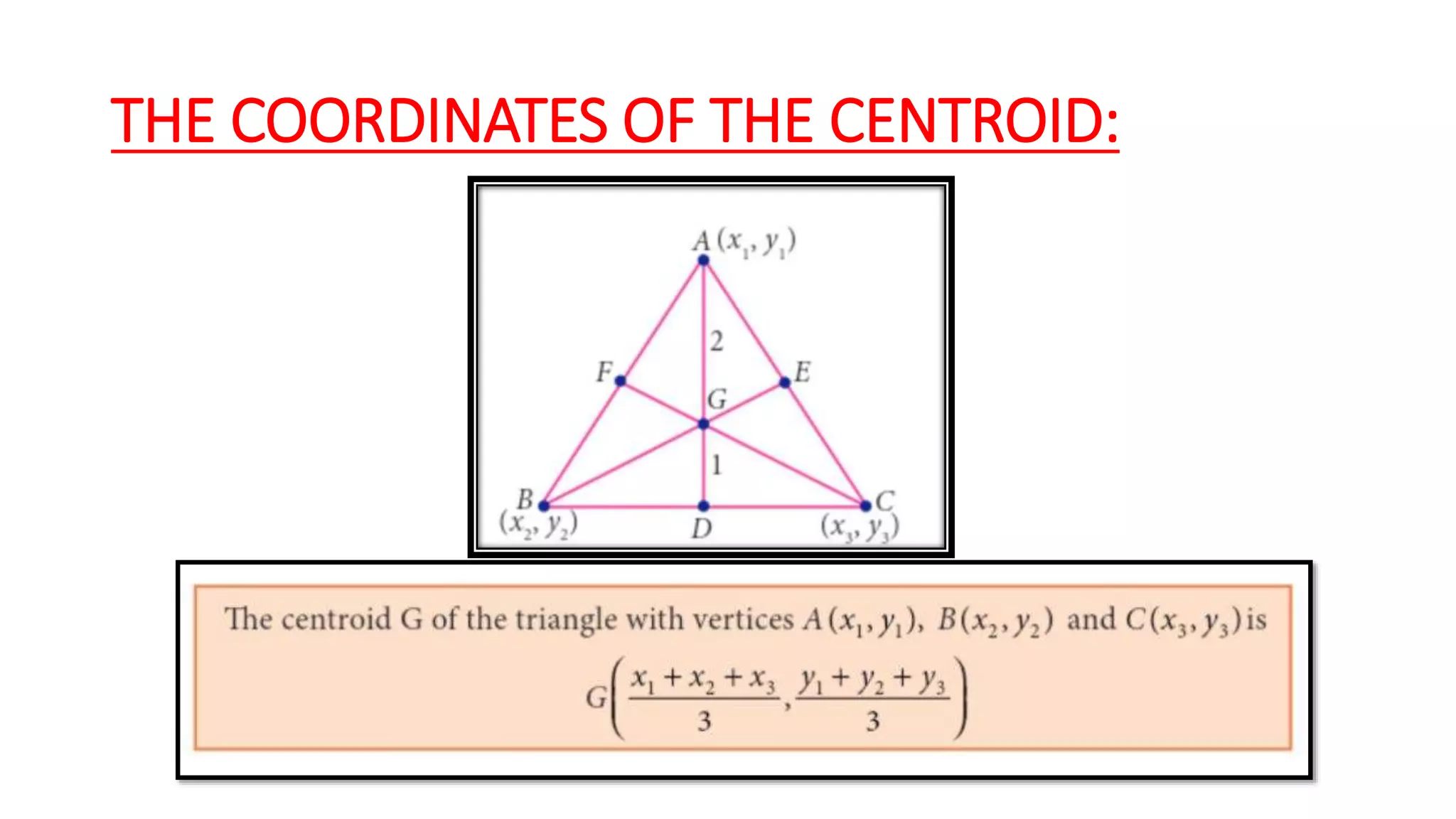
Coordinate geometry is a system that describes the position of points on a plane using ordered pairs of numbers. Rene Descartes developed this branch of mathematics in the 17th century. A coordinate plane has two perpendicular axes (x and y) that intersect at the origin point (0,0). The distance between any two points on the plane can be calculated using the Pythagorean theorem. The midpoint and points of trisection of a line segment can be found using section formulas, as can the coordinates of the centroid of a figure.

1. STANDARD NINE
TERM-II
MATHEMATICS
CO-ORDINATE GEOMETRY
By,
DARSHINI.A.

2. CONTENTS
• What is co-ordinate geometry?
• Devising a co-ordinate system
• Distance between any two points
• Properties of distance
• The midpoint of a line segment
• Points of trisection of a line segment
• Section Formula
• The coordinates of the centroid

3. What is co-ordinate geometry?

4. A system of geometry where the position of points on the
plane is described using an ordered pair of numbers.

5. FOUNDER OF CO-ORDINATE GEOMETRY

6. The French Mathematician Rene Descartes (1596-
1650) developed a new branch of mathematics called
the Analytical Geometry or Co-ordinate Geometry
which combined all arithmetic, algebraic and
geometry of the past ages in a single technique of
visualising as points on a graph and equations as
geometrical shapes.

7. DEVISING A CO-ORDINATE SYSTEM:
Co-ordinate plane:
It has two scales – one running across the plane called the
“x-axis” and another a right angle to it called the “y-axis”.
The point where the axes cross is called the “Origin” and is
where both x and y are zero.

10. The x co-ordinate Is called the Abscissa and the y
co-ordinate is called the Ordinate.
The x-axis and the y-axis divide the plane into
four regions called the Quadrants.They are usually
numbered as I, II, III and IV.

13. The “straight line distance” is usually called as “the crow flies”.
1. Distance between two points on the co-ordinate axes
2. Distance between two points lying on a line parallel to coordinate
axes
3. Distance between two Points on a plane
DISTANCE BETWEEN ANY TWO POINTS:

14. Distance between two points on the co-ordinate
axes:
Points on x-axis:
If two points lie on the x-axis ,
then the distance between them
is equal to the difference
between the x co-ordinates.
Points on y-axis:
If two points lie on the y-axis,
then the distance between them
is equal to the difference between
the y co-ordinates.

15. Distance between two points on a plane:

16. Properties of distance:
• The sum of the distance between two pairs of points is equal to the
third pair of points. In other words, points A, B, C are collinear if
AB+BC=AC.
• The sum of the squares of two sides is equal to the square of the third
side , which is the hypotenuse of a right angled triangle.
• The opposite sides of a parallelogram are equal.

17. THE MIDPOINT OF A LINE SEGMENT:

18. POINTS OF TRISECTION OF A LINE SEGMENT:

19. SECTION FORMULA:

21. THE COORDINATES OF THE CENTROID: