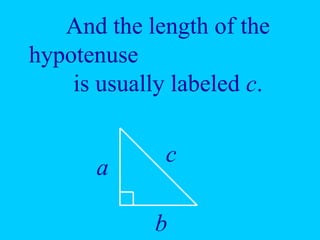
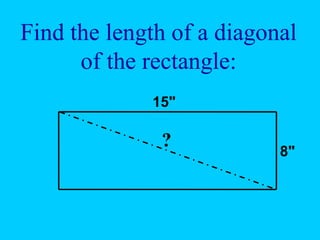
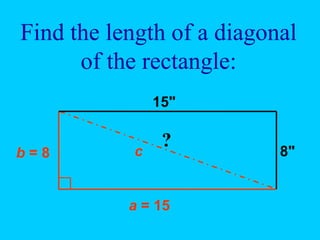
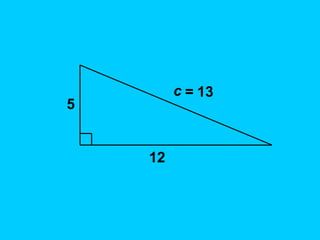
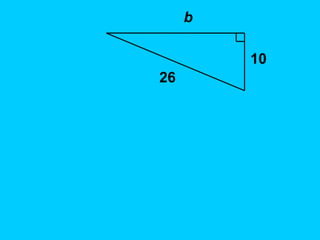
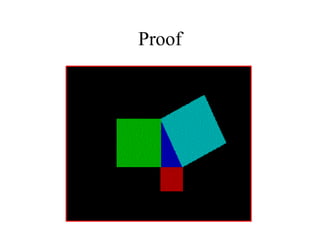
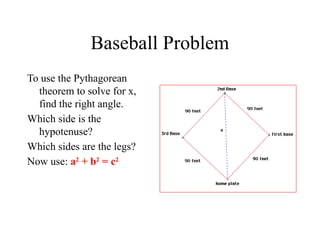
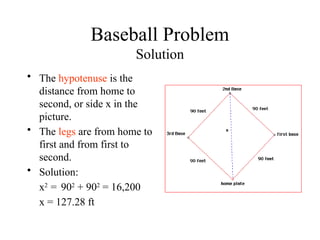
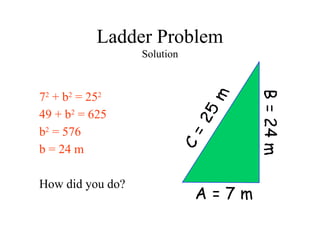
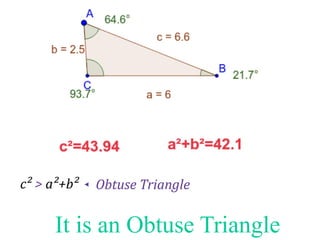
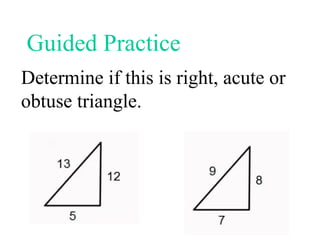
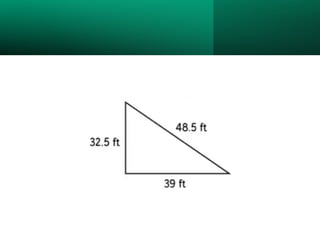
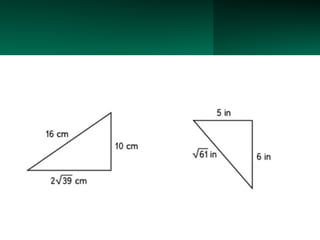
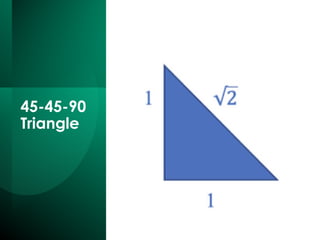
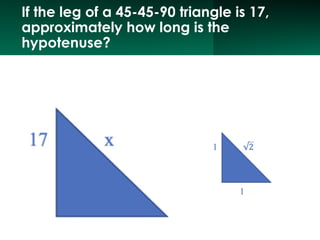
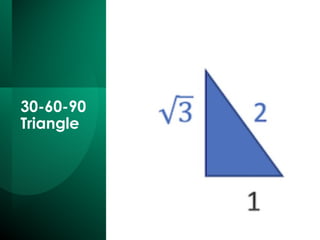
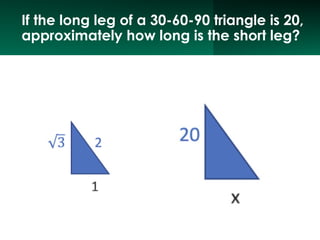
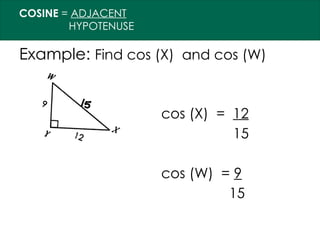
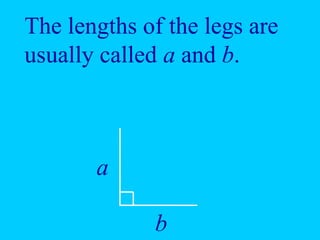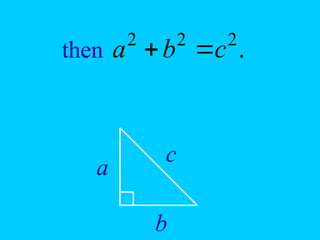The document discusses the Pythagorean Theorem, illustrating its application in various real-life scenarios, such as calculating distances involving right triangles. It includes examples, exercises, and problems related to right triangles, including how to apply trigonometric ratios. Additionally, it provides practical applications and scenarios, including architecture and surveying tasks that utilize the theorem.

1. a
b
c
2
2
2
c
b
a 

THE PYTHAGOREAN
THEOREM

2. Pythagorean Theorem
Essential Questions
How is the Pythagorean Theorem
used to identify side lengths?
When can the Pythagorean
Theorem be used to solve real life
patterns?

3. This is a right triangle:

4. The two sides which
come together in a right
angle are called

5. The two sides which
come together in a right
angle are called

6. The two sides which
come together in a right
angle are called

7. The lengths of the legs are
usually called a and b.
a
b

8. The side across from the
right angle
a
b
is called the

9. And the length of the
hypotenuse
is usually labeled c.
a
b
c

10. The relationship Pythagorus
discovered is now called
The Pythagorean Theorem:
a
b
c

11. The Pythagorean Theorem
says, given the right triangle
with legs a and b and
hypotenuse c,
a
b
c

12. then
a
b
c
.
2
2
2
c
b
a 


13. You can use The Pythagorean
Theorem to solve many kinds
of problems.
Suppose you drive directly
west for 48 miles,
48

14. Then turn south and drive for
36 miles.
48
36

15. How far are you from where
you started?
48
36
?

16. 482
Using The Pythagorean
Theorem,
48
36
c
362
+ = c2

17. Find the length of a diagonal
of the rectangle:
15"
8"
?

18. Find the length of a diagonal
of the rectangle:
15"
8"
?
b = 8
a = 15
c

19. 2
2
2
c
b
a 
 2
2
2
8
15 c

 2
64
225 c

 289
2

c 17

c
b = 8
a = 15
c

20. Find the length of a diagonal
of the rectangle:
15"
8"
17

21. Practice using
The Pythagorean Theorem
to solve these right triangles:

22. 5
12
c = 13

23. 10
b
26

24. 10
b
26
= 24
(a)
(c)
2
2
2
c
b
a 

2
2
2
26
10 
b
676
100 2

b
100
676
2


b
576
2

b
24

b

25. Check It Out! Example 2
A rectangular field has a length of 100 yards and a
width of 33 yards. About how far is it from one corner
of the field to the opposite corner of the field? Round
your answer to the nearest tenth.
100 y
33 y ?

26. Check It Out! Solution
Solve
a2
+ b2
= c2
332
+ 1002
= c2
1089 + 10,000 = c2
11,089 = c2
105.304  c
The distance from one corner of the field to the
opposite corner is about 105.3 yards.
Use the Pythagorean Theorem.
Substitute for the known variables.
Evaluate the powers.
Add.
Take the square roots of both sides.
105.3  c Round.

27. The Pythagorean Theorem
“For any right triangle,
the sum of the areas of
the two small squares is
equal to the area of the
larger.”
a2
+ b2
= c2

28. Proof

29. a
a
a2
b
b
c
c
b2
c2
Let’s look at it
this way…

30. Baseball Problem
A baseball “diamond” is really a square.
You can use the Pythagorean theorem to find
distances around a baseball diamond.

31. Baseball Problem
The distance between
consecutive bases is 90
feet. How far does a
catcher have to throw
the ball from home
plate to second base?

32. Baseball Problem
To use the Pythagorean
theorem to solve for x,
find the right angle.
Which side is the
hypotenuse?
Which sides are the legs?
Now use: a2
+ b2
= c2

33. Baseball Problem
Solution
• The hypotenuse is the
distance from home to
second, or side x in the
picture.
• The legs are from home to
first and from first to
second.
• Solution:
x2
= 902
+ 902
= 16,200
x = 127.28 ft

34. Ladder Problem
A ladder leans against a
second-story window of a
house.
If the ladder is 25 meters
long,
and the base of the ladder
is 7 meters from the
house,
how high is the window?

35. Ladder Problem
Solution
• First draw a diagram that
shows the sides of the
right triangle.
• Label the sides:
– Ladder is 25 m
– Distance from house is 7
m
• Use a2
+ b2
= c2
to solve
for the missing side.
Distance from house: 7 meters

36. Ladder Problem
Solution
72
+ b2
= 252
49 + b2
= 625
b2
= 576
b = 24 m
How did you do?
A = 7 m

37. Task to Practice:
1. A park has a walking path that
forms a right triangle. The lengths of
the legs are 8 meters and 15 meters.
Find the length of the diagonal path.
2. A boat travels 12 miles north and 16
miles east. How far is the boat from its
starting point?

38. Peer Collaboration
Make a scenario on which you can
apply Pythagorean theorem in your
daily life going to school.
Illustrate the problem and solve.

39. REVIEW ON
PYTHAGOREAN
THEOREM

40. • A 15-foot tree casts a shadow that is 9
feet long. How long is from the top of the
tree to the tip of the shadow, if the
ground is flat and the tree and its shadow
form a right triangle?
15 ft
9 ft

41. Illustrate
and
solve:
• An airplane is flying
directly from point A
to point B, passing
over the top of a
mountain. The
horizontal distance
from A to B is 400
miles, and the
mountain is 300
miles tall. What is the
straight-line distance
from point A to point
B?

42. • A rectangular garden
has a length of 12
meters and a width of
9 meters. What is the
length of the
diagonal?

43. • Is the triangle with
sides 8, 15, and 17 a
right triangle?

44. PEER ACTIVITY
• Given the worksheet,
brainstorm how to
solve the given real-
world problem, show
your solution.

45. CONVERSE OF
PYTHAGOREAN THEOREM

46. Generally, if

47. It is a right triangle

48. It is an Obtuse Triangle

49. c2
= 92
= 81
a2
+ b2
=82
+ 72
= 113
It is an Acute Triangle
81 < 113

50. Determine if this is right, acute or
obtuse triangle.
Guided Practice

53. INDEPENDENT
ACTIVITY

54. SPECIAL
RIGHT
TRIANGLE

55. 45-45-90
Triangle

56. If the leg of a 45-45-90 triangle is 17,
approximately how long is the
hypotenuse?

57. 30-60-90
Triangle

58. If the long leg of a 30-60-90 triangle is 20,
approximately how long is the short leg?

59. REVIEW
OF
SPECIAL
RIGHT
TRIANGLE
300
-600
-900
Triangle
450
-450
-900
Triangle

60. APPLICATION OF SPECIAL RIGHT
TRIANGLE
An 18-foot ladder is leaning against a wall, forming a 30°
angle with the wall and the foot of the ladder form 600
with the ground. How high up the wall does the ladder
reach?
300
600
18 ft
x

61. APPLICATION OF SPECIAL RIGHT
TRIANGLE
Cutting a Square in Half
A square has sides of 10 units. If you cut the
square in half along its diagonal, what is the
length of the diagonal?

62. APPLICATION OF SPECIAL RIGHT
TRIANGLE
• A six-ft-long door jam leans against a building. If the
door jam makes an angle of 60° with the ground, how
far up the wall does the jam reach? How far from the
wall is the base of the jam? Round your answers to two
decimal places, as needed.
600
6ft
y
x

63. THINK-
PAIR-
SHARE
ACTIVITY
Analyze the
problem
Illustrate the
scenario.
Solve the missing
side of the
triangle.
Explain your
answer.

64. REVIEW
Samantha is designing a
triangular garden in the
shape of a 30-60-90 special
right triangle. The shortest
side of the triangle,
opposite the 30° angle, is 10
feet long.
1. What is the length of the
hypotenuse?
2. What is the length of the
longer leg, opposite the 60°
angle?

65. Trigonometric
Ratios
Trigonometry is the
study of triangle
measurement.

66. TRIGONOMETRIC RATIOS
Every acute angle of a right triangle has
the following trigonometric ratios:

67. TRIGONOMETRIC RATIOS
SINE = The ratio of the leg opposite the
angle to the hypotenuse.
SIN A = a
c
SIN B = b
c

68. Example: Find sin (X) and sin (W)
Sin (X) = 9
15
Sin (W) = 12
15
SINE = opposite
hypotenuse

69. TRIGONOMETRIC RATIOS
COSINE = The ratio of the leg adjacent to
the angle to the hypotenuse.
COS A = b
c
COS B = a
c

70. Example: Find cos (X) and cos (W)
cos (X) = 12
15
cos (W) = 9
15
COSINE = ADJACENT
HYPOTENUSE

71. TRIGONOMETRIC RATIOS
TANGENT = The ratio of the leg opposite
the angle to the leg adjacent to the angle.
TAN A = a
b
TAN B = b
a

72. Example: Find sin (X) and sin (W)
tan (X) = 9
12
tan (W) = 12
9
Tangent = opposite
adjacent

73. Example
Find:
1. Sin A
2. Sin C
3. Cos A
4. Cos C
5. Tan A
6. Tan C
Remember

74. Give each trigonometric ratio as
a fraction in simplest form.

75. Find the Angle.
Sin A _____ Cos C_____
Cos B ____ Tan A _____
Tan C _____ Sin B _____

76. REVIEW
A ladder in leaning against a building.
The length of the ladder is 25 ft. The point
where the ladder touches the side of the
building is 20 ft above the ground. What is
the measure of the angle formed by the
ground and the ladder?
20ft
25ft

77. REVIEW
A statue is 46ft tall. Greg is standing 110 ft
from the base of the statue. What is angle
made by the ground and the line to the
top of the statue from where Greg is
standing
46ft
110 ft

78. REAL-WORLD PROBLEM APPLICATION
You’re designing a ramp for a new wheelchair-accessible
building. The ramp needs to have a safe and comfortable
slope, and you're working with the following specifications:
• The ramp must rise 4 feet (the height from the ground to
the entrance of the building).
• The ramp must have a total length of 20 feet, which is the
hypotenuse of the right triangle you’ll use for the ramp
design.
Task:
1.Find the horizontal distance (the base of the triangle) between
the base of the ramp and the building.
2.Determine the angle measure that the ramp makes with the
ground.
3.Using the values from the ramp, calculate the six trigonometric
ratios for the angle of elevation.

79. REAL-WORLD PROBLEM APPLICATION
You are a surveyor working on a project to map a piece of land.
You need to measure the distance between two points, A and B,
across a river, but the area is difficult to access directly. Instead,
you can measure the distance between points A and C on the
same side of the river, and also the angle formed by the ground
to a point directly above point B.
• The distance between point A and C (along the riverbank) is
100 meters.
• The angle measure by the ground to point B is 30°.
• The distance from point A to a point directly above B (height
from the water level to the top of the point) is 50 meters.
Task:
• Find the distance between points A and B across the river.
• Using the given angle measure , calculate the horizontal
distance between point C and the top of point B (the "height"
distance from the river level).
• Find all six trigonometric ratios for the angle at point C.