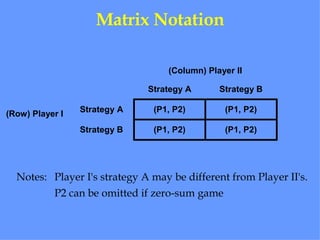
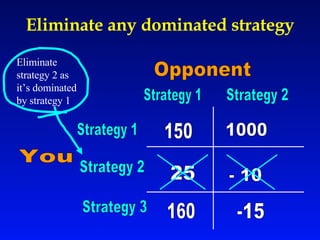
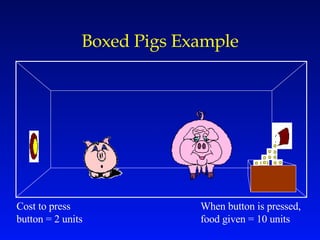
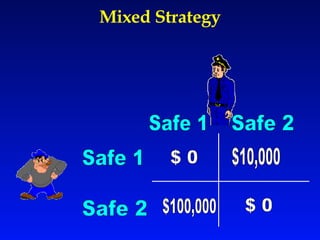
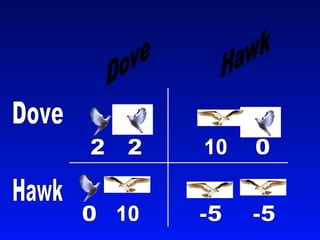
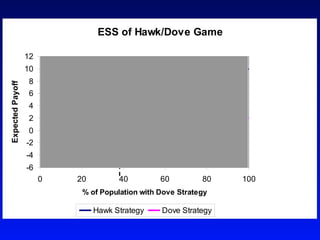
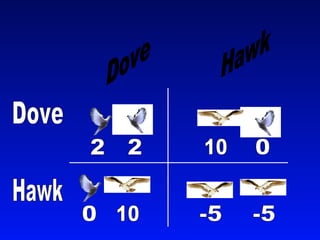
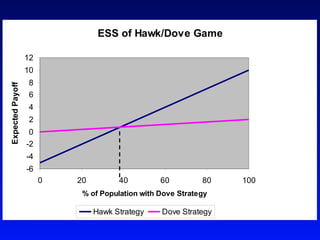
Game theory is a mathematical approach to modeling strategic interactions between rational decision-makers. It assumes humans seek the best outcomes and makes predictions based on payoff matrices showing players' rewards for different strategy combinations. Common applications include economics, politics, and analyzing conflict and cooperation situations like the Prisoner's Dilemma. Game theory also studies concepts like Nash equilibrium, mixed strategies, and evolutionary stable strategies.

1. Introduction to Game Theory Yale Braunstein Spring 2007

15. Matrix Notation Notes: Player I's strategy A may be different from Player II's. P2 can be omitted if zero-sum game

16. Prisoner’s Dilemma & Other famous games A sample of other games: Marriage Disarmament (my generals are more irrational than yours)

17. Prisoner’s Dilemma 10 , 10 Blame Don't Blame Don't 20 , 0 0 , 20 1 , 1 Prisoner 1 Prisoner 2 Notes: Higher payoffs (longer sentences) are bad. Non-cooperative equilibrium  Joint maximum Institutionalized “solutions” (a la criminal organizations, KSM) NCE Jt. max.

22. Plan ahead and look back Strategy 2 Strategy 1 150 1000 25 Strategy 1 Strategy 2 - 10 You Opponent

23. If you have a dominating strategy, use it Strategy 2 Strategy 1 150 1000 25 Strategy 1 Strategy 2 - 10 You Opponent Use strategy 1

24. Eliminate any dominated strategy Strategy 2 Strategy 1 150 1000 25 Strategy 1 Strategy 2 - 10 You Opponent Strategy 3 -15 160 Eliminate strategy 2 as it’s dominated by strategy 1

27. Maximin & Minimax Equilibrium Strategies Strategy 2 Strategy 1 150 1000 25 Strategy 1 Strategy 2 - 10 You Opponent Strategy 3 -15 160 Min 1000 150 - 10 -15 160 Max

29. Is this a Nash Equilibrium? Strategy 2 Strategy 1 150 1000 25 Strategy 1 Strategy 2 - 10 You Opponent Strategy 3 -15 160 Min 1000 150 - 10 -15 160 Max

30. Cost to press button = 2 units When button is pressed, food given = 10 units Boxed Pigs Example

31. 5 , 1 Press Wait Press Wait 9 , -1 4 , 4 0 , 0 Little Pig Big Pig Decisions, decisions...

33. Mixed Strategy Safe 2 Safe 1 $ 0 $10,000 $100,000 Safe 1 Safe 2 $ 0

34. Mixed Strategy Solution

35. The Payoff Matrix for Holmes & Moriarity Player #1 Player #2 Strategy #1 Strategy #2 Strategy #1 Strategy #2 Payoff (1,1) Payoff (1,2) Payoff (2,1) Payoff (2,2) Canterbury Canterbury Dover Dover 0 100 50 0 Holmes Moriarty

37. Hawk / Dove Game

39. Hawk Dove Hawk Dove 2 2 10 0 10 0 -5 -5

41. Hawk Dove Hawk Dove 2 2 10 0 10 0 -5 -5