Game theory
•Download as PPT, PDF•
6 likes•4,141 views
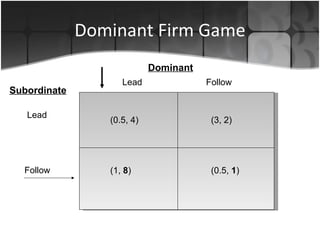
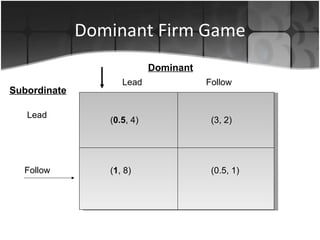
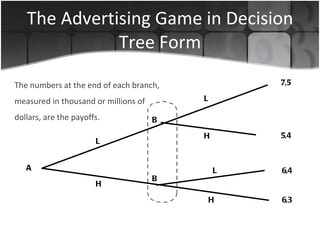
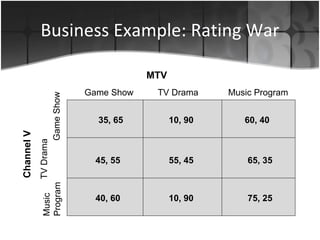
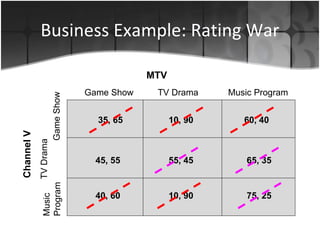
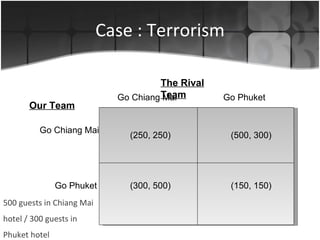
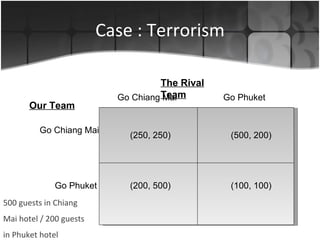
The document discusses several applications of game theory including the dominant firm game, Nash equilibrium, prisoner's dilemma, and a terrorism scenario. It analyzes strategic situations involving two or more players where the success of each player depends on the choices of others. Key concepts explained are dominant strategies, Nash equilibria, and how game theory can model real-world competitive interactions and predict outcomes even when players cannot communicate.
![Game Theory ,[object Object]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Recommended
More Related Content
What's hot
What's hot (20)
Viewers also liked
Similar to Game theory
Similar to Game theory (20)
Recently uploaded
Recently uploaded (20)
Game theory
- 1. GAME THEORY AN APPLICATION
- 6. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow (0.5, 4) (1, 8) (3, 2) (0.5, 1)
- 7. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow (0.5, 4 ) (1, 8) (3, 2 ) (0.5, 1)
- 8. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow (0.5, 4) (1, 8 ) (3, 2) (0.5, 1 )
- 10. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow (0.5, 4) (1, 8) ( 3 , 2) ( 0.5 , 1)
- 11. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow ( 0.5 , 4) ( 1 , 8) (3, 2) (0.5, 1)
- 13. Dominant Firm Game Lead Follow Dominant Subordinate Lead Follow (0.5, 4) ( 1 , 8 ) (3, 2) (0.5, 1)
- 15. NASH EQUILIBRIUM
- 17. CASE I: APPLICATION OF GAME THEORY IN TWO ADVERTISING AGENCIES
- 20. The Advertising Game in Decision Tree Form The numbers at the end of each branch, measured in thousand or millions of dollars, are the payoffs. 7,5 L L H L H H B B A 5,4 6,4 6,3
- 27. CASE II: APPLICATION OF GAME THEORY IN TWO TELEVISION CHANNELS
- 28. Business Example: Rating War 35, 65 10, 90 60, 40 45, 55 55, 45 65, 35 75, 25 10, 90 40, 60 MTV Channel V Game Show TV Drama Music Program Game Show TV Drama Music Program
- 29. Business Example: Rating War 35, 65 10, 90 60, 40 45, 55 55, 45 65, 35 75, 25 10, 90 40, 60 MTV Channel V Game Show TV Drama Music Program Game Show TV Drama Music Program
- 37. Case : Terrorism 500 guests in Chiang Mai hotel / 300 guests in Phuket hotel Go Chiang Mai Go Phuket The Rival Team Our Team Go Chiang Mai Go Phuket (250, 250) (300, 500) (500, 300) (150, 150)
- 44. Case : Terrorism 500 guests in Chiang Mai hotel / 200 guests in Phuket hotel Go Chiang Mai Go Phuket The Rival Team Our Team Go Chiang Mai Go Phuket (250, 250) (200, 500) (500, 200) (100, 100)
- 48. A PRESENTATION BY: Amritanshu Mehra (11DCP008) Kush Aggarwal (11DCP024) Ravi Gupta (11DCP038 )