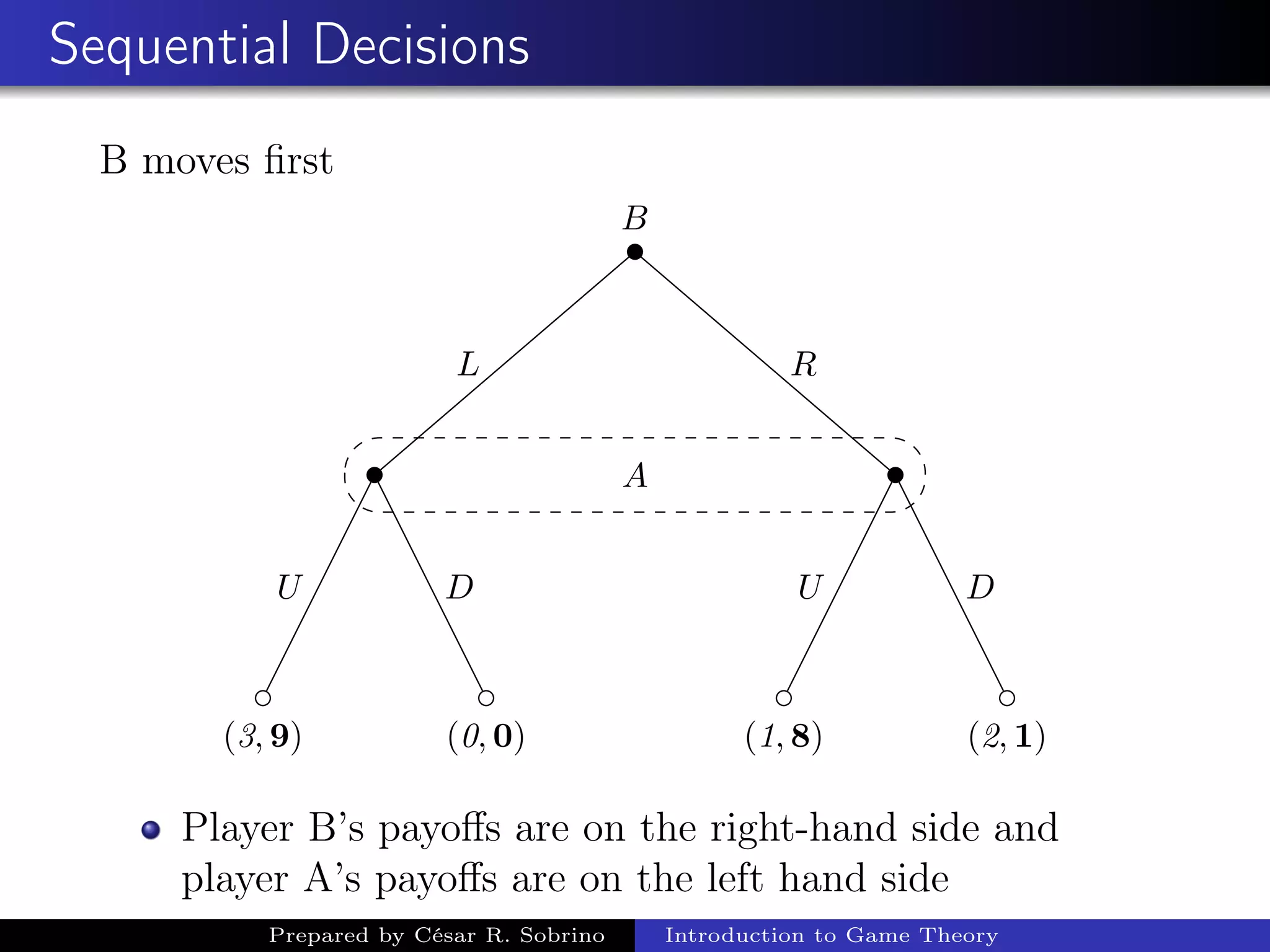
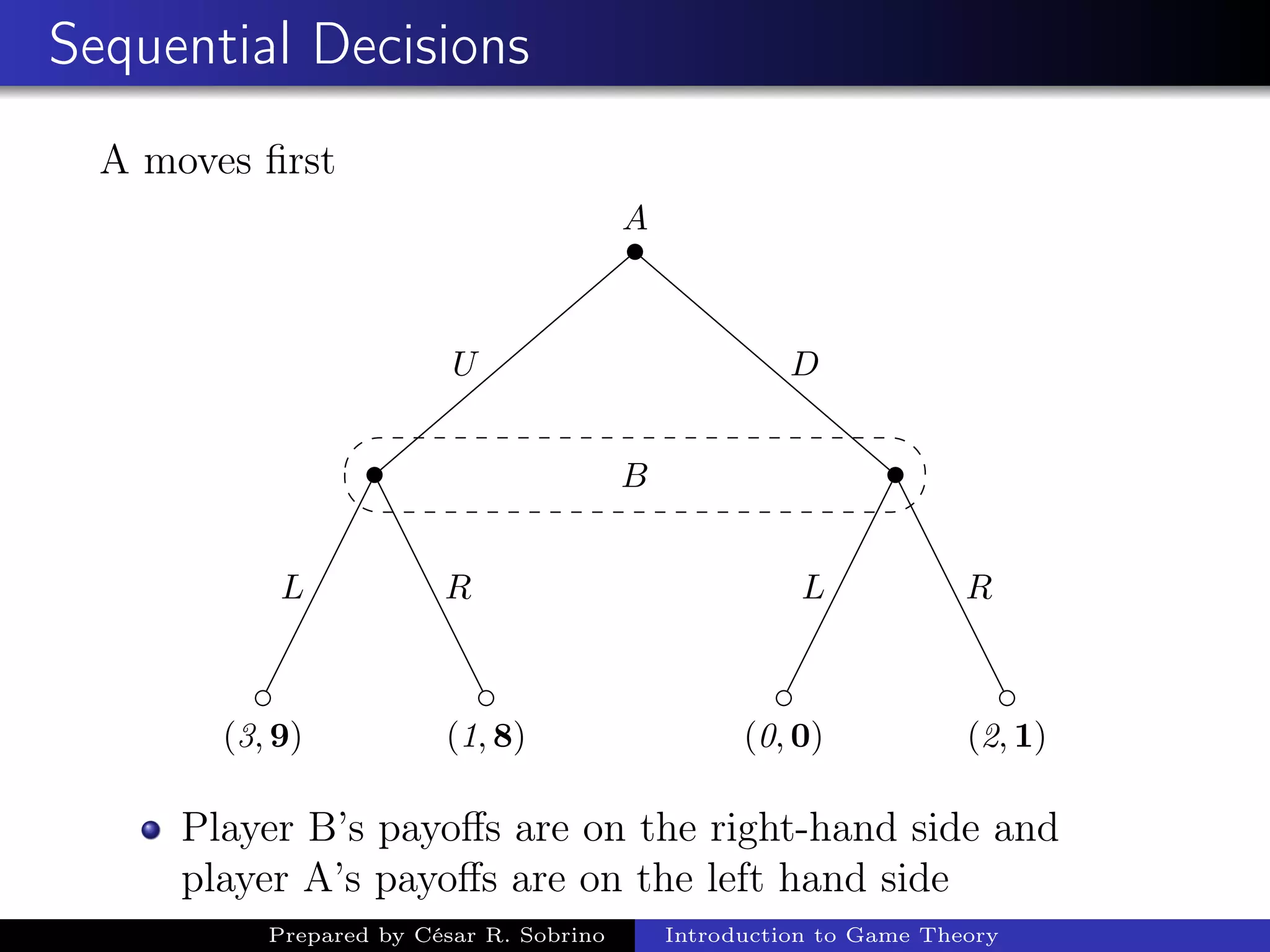
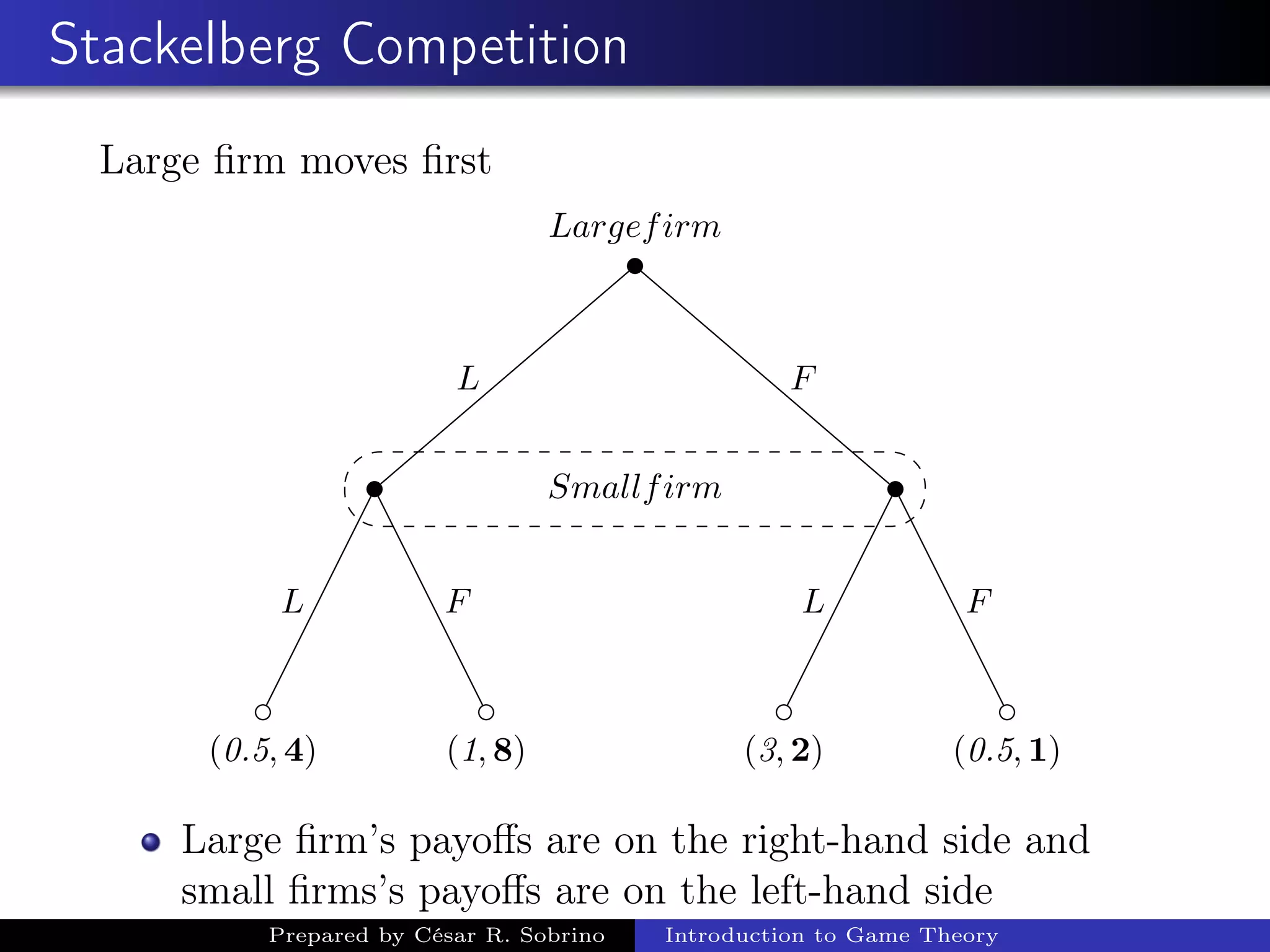
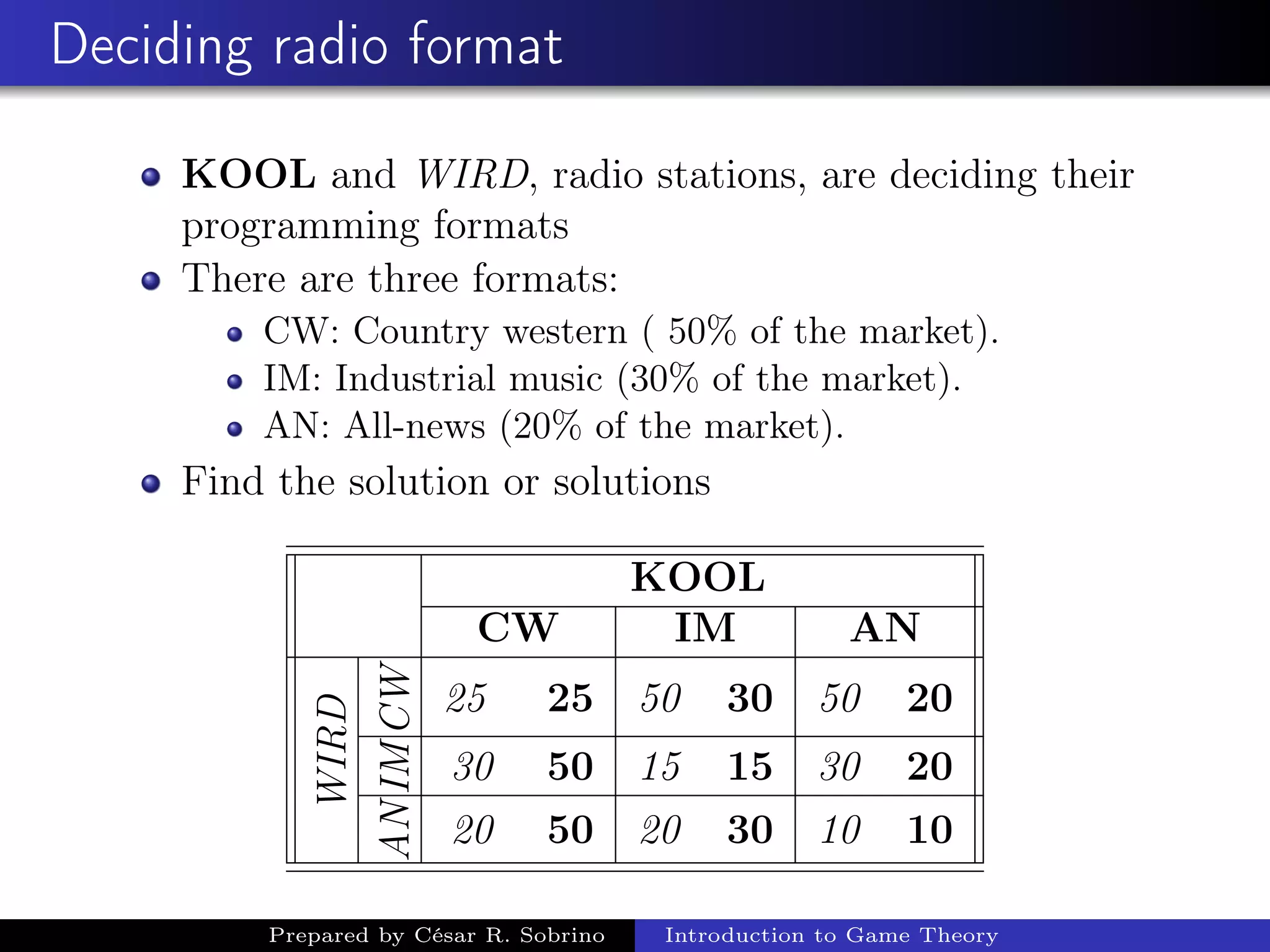
This document provides an introduction and overview of game theory. It describes key concepts in game theory including the elements of a game, complete and incomplete information, perfect and imperfect information, Nash equilibrium, simultaneous decisions, pure strategies and dominant strategies. It provides examples of classic games including the prisoner's dilemma, trade war, and battle of the sexes to illustrate these concepts. The prisoner's dilemma and trade war examples show how the games have dominant strategies that lead to a Nash equilibrium that is not optimal for either player.








































![Skeeping Employees from Shirking
Suppose:
Employee chooses (work, shirk) with probabilities
(p,1 − p), respectively. p ∈]0, 1[.
Manager chooses (monitor, no monitor) with
probabilities (q,1 − q), respectively. q ∈]0, 1[
First, find employee’s expected payoff from each pure
strategy.
If employee works: receives 50
E(work)= 50 × q + 50 × (1 − q) = 50
If employee shirks: receives 0 or 100
E(shirk)=0 × q + 100 × (1 − q) = 100 − 100 × q
Prepared by César R. Sobrino Introduction to Game Theory](https://image.slidesharecdn.com/introductiontogametheory-180822214434/75/Introduction-to-Game-Theory-42-2048.jpg)