Downloaded 80 times
Uploaded byNjdeh Tahmasian
Game Theory: An Intoduction
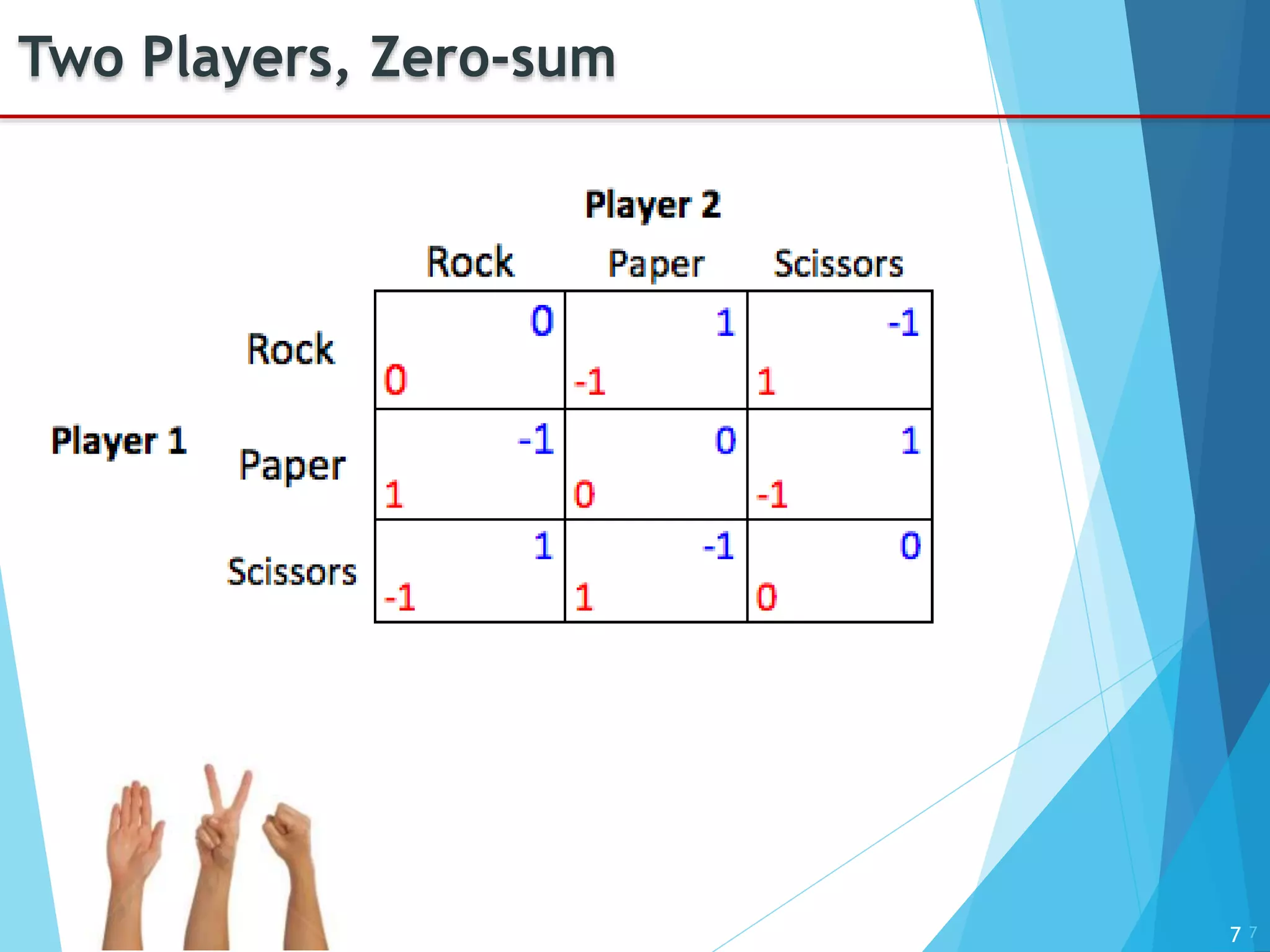
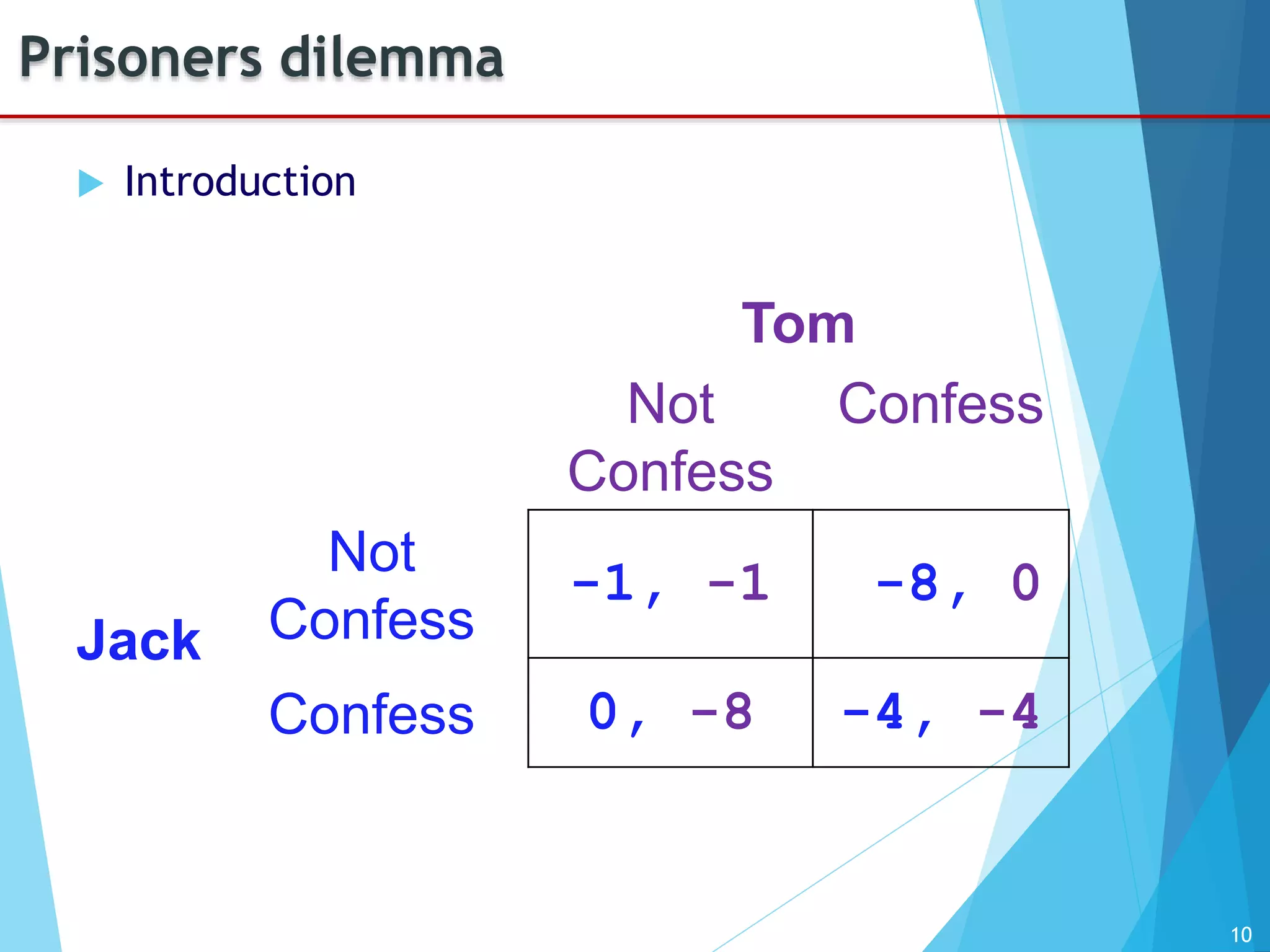
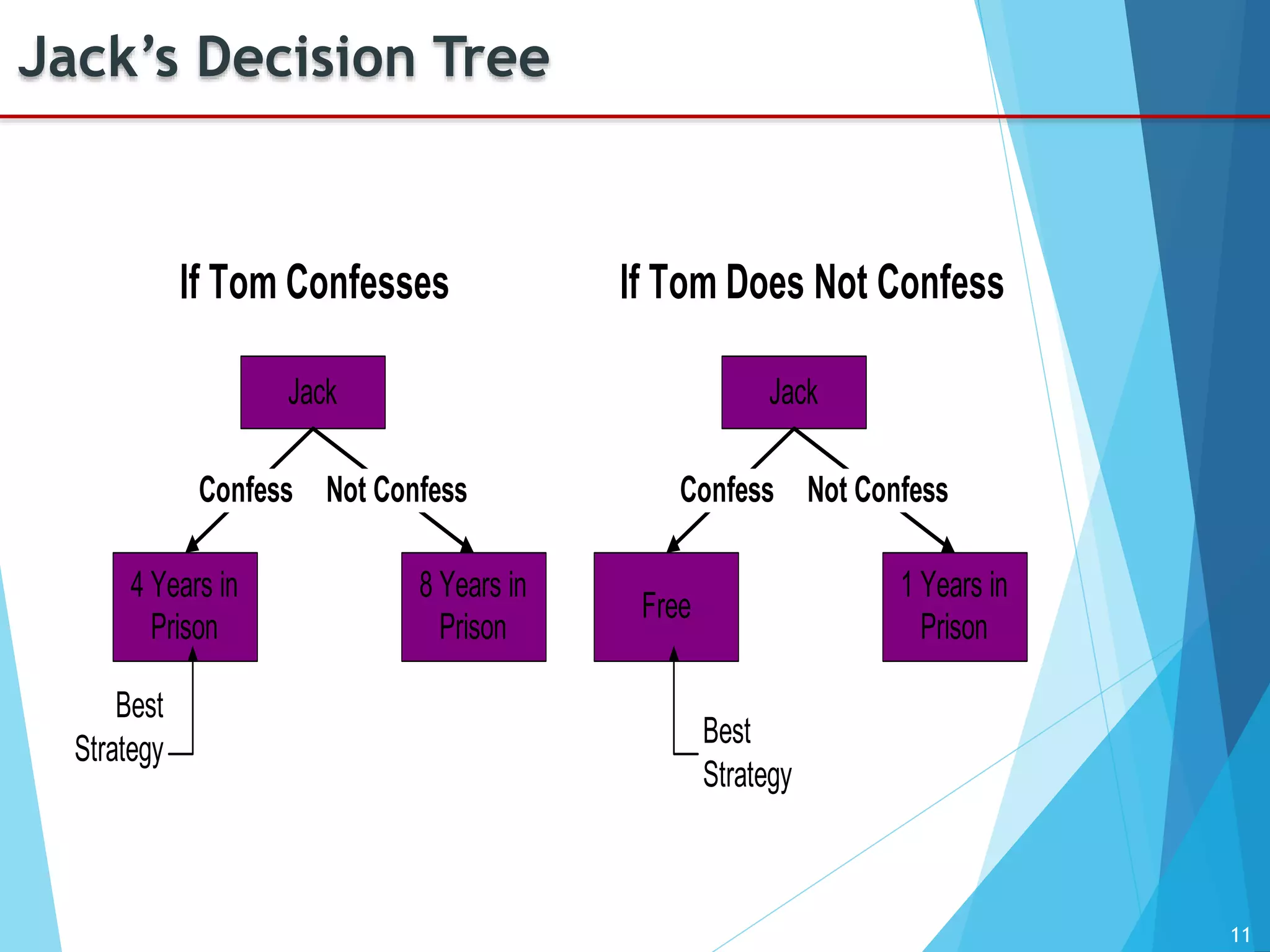
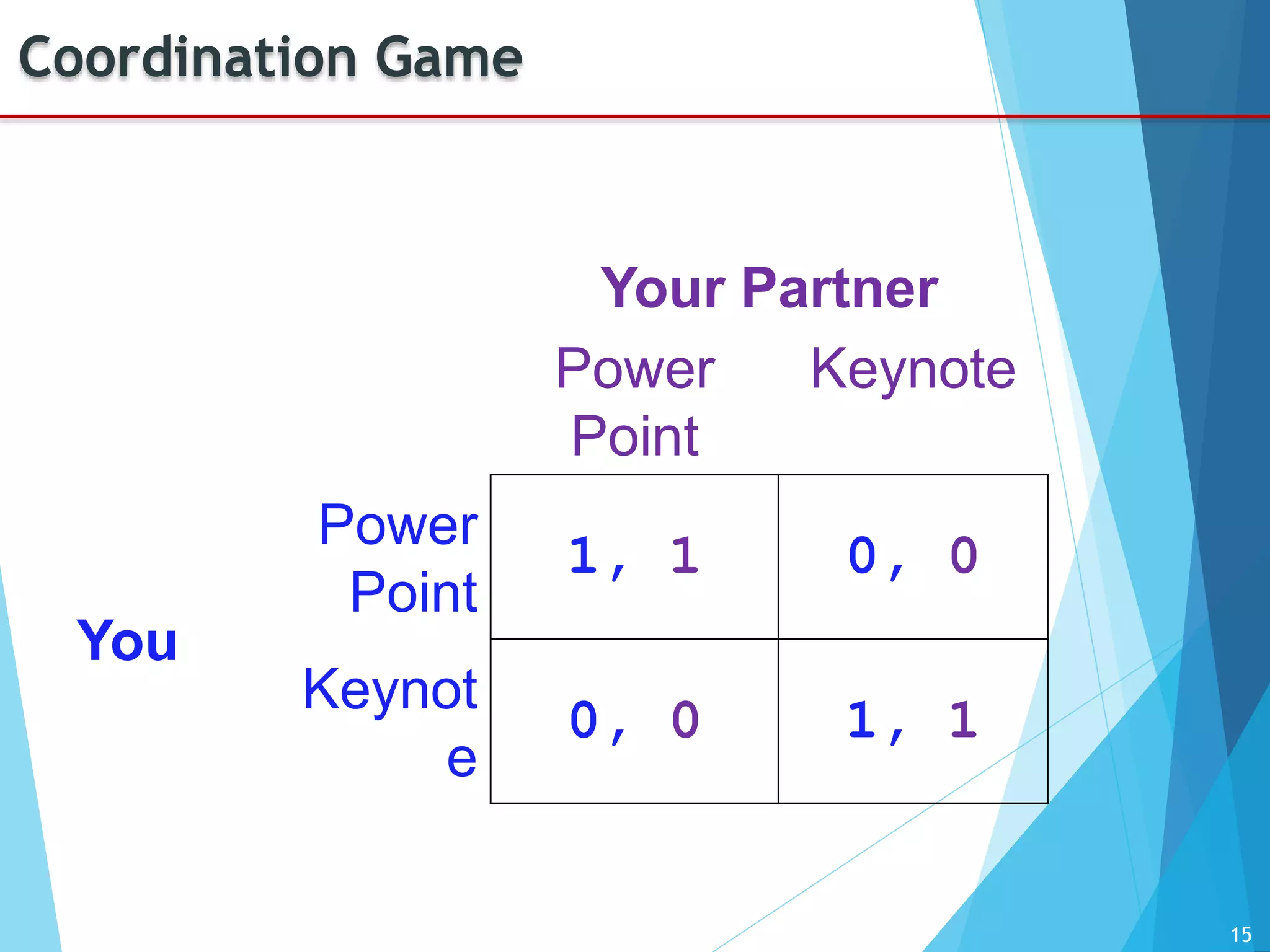
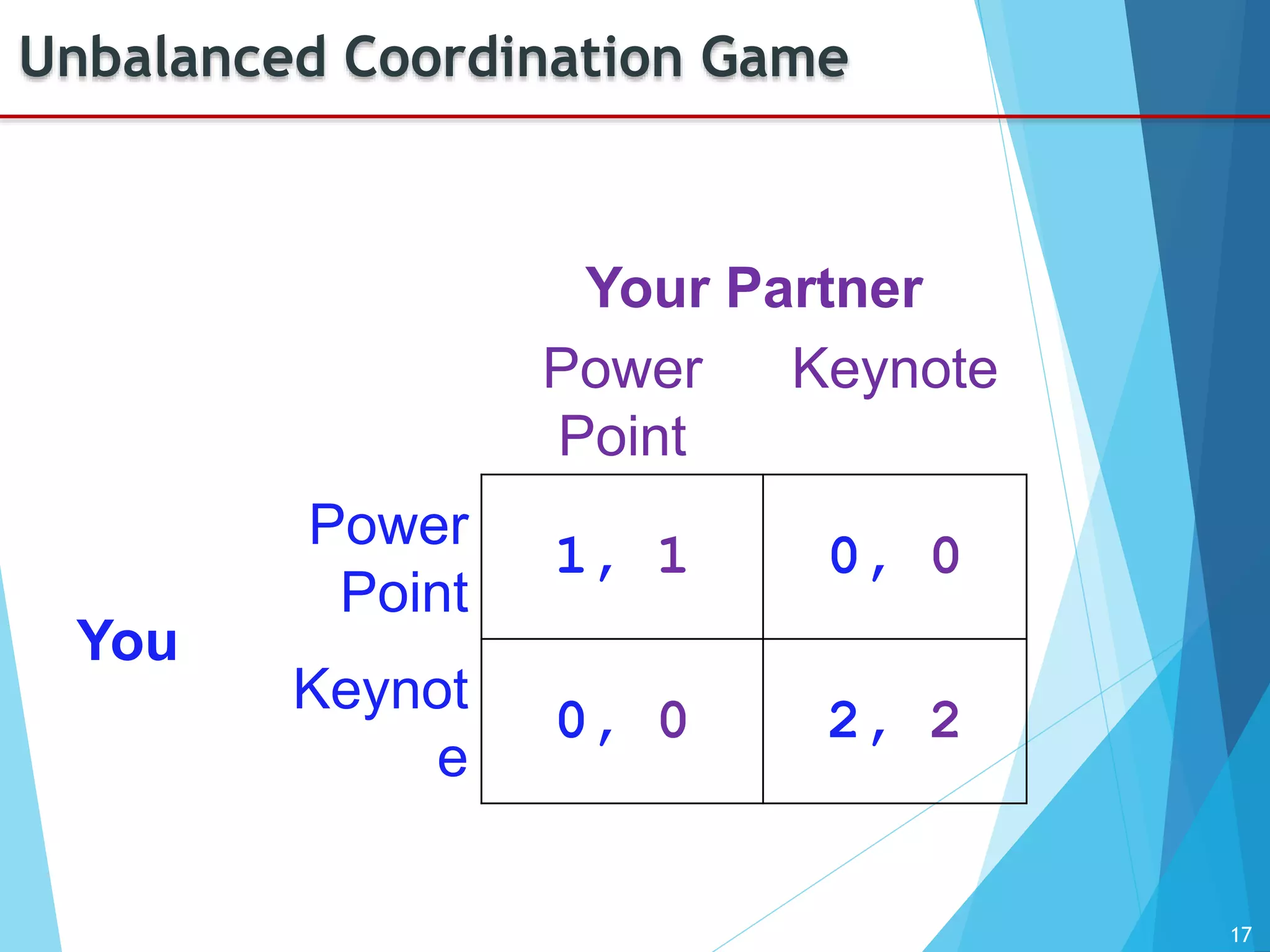
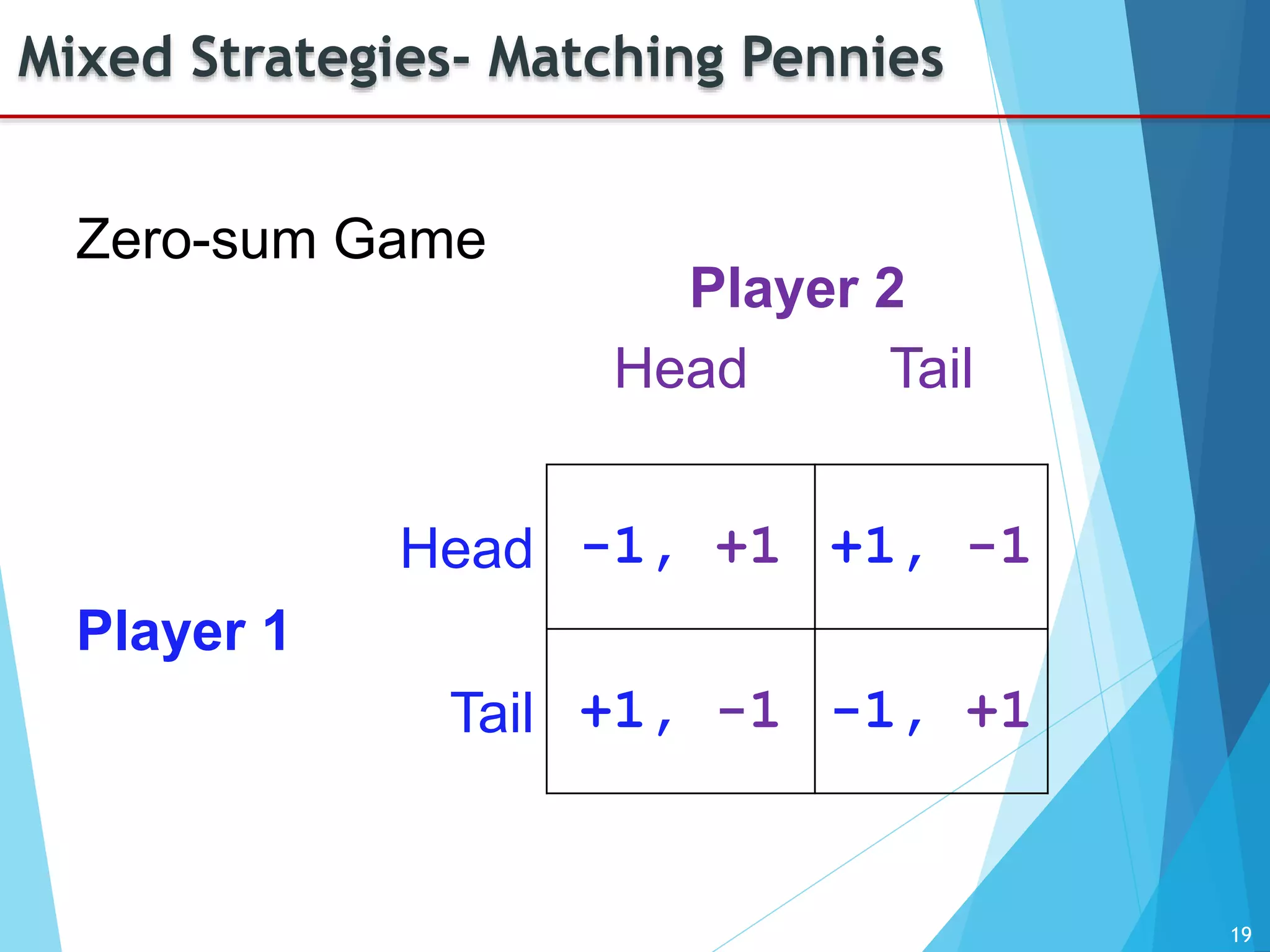
The document provides an introduction to game theory, detailing its history, applications, and key concepts such as the prisoner's dilemma, dominant strategies, and Nash equilibrium. It highlights the interdisciplinary nature of game theory, developed since the 1920s, and its relevance in various fields including economics, politics, and sports. The document also explores different types of games and their classifications based on player interaction and information availability.
More Related Content
Similar to Game Theory: An Intoduction
Game Theory: An Intoduction
- 1. 1 GAME THEORY AN INTRODUCTION NjdehTahmasian Savarani Winter 2014
- 2. 2 History Interdisciplinary (Economicand Mathematic) approach to the study of human behavior Founded in the 1920s by John von Neumann 1994 Nobel prize in Economics awarded to three researchers “Games” are a metaphor for wide range of human interactions
- 3. 3 Applications Market: pricingof a new product when other firms have similar new products deciding how to bid in an auction Networking: choosing a route on the Internet or through a transportation networks Politic: Deciding whether to adopt an aggressive or a passive stance in international relations Sport: choosing how to target a soccer penalty kick and choosing how to defend against Choosing whether to use performance-enhancing drugs in a professional sport 3
- 4. 4 What is a(Mathematical) Game? Rules Outcomes and payoffs Uncertainty of the Outcome Decision making No cheating 4
- 5. 5 Classification of Games Number of players Simultaneous or sequential game Random moves Perfect information Complete information Zero-sum games Communication Cooperative or non-cooperative game 5
- 6.
- 7.
- 8. 8 Three or MorePlayers
- 9. 9 The Prisoner’s Dilemma Two burglars, Jack and Tom, are captured and separated by the police Each has to choose whether or not to confess and implicate the other If neither confesses, they both serve one year for carrying a concealed weapon If each confesses and implicates the other, they both get 4 years If one confesses and the other does not, the confessor goes free, and the other gets 8 years
- 10. 10 Prisoners dilemma Introduction Tom Not Confess Confess Jack Not Confess -1,-1 -8, 0 Confess 0, -8 -4, -4
- 11. 11 Jack’s Decision Tree IfTom Does Not ConfessIf Tom Confesses Jack 4 Years in Prison 8 Years in Prison Free 1 Years in Prison Jack Not ConfessConfess Confess Not Confess Best Strategy Best Strategy
- 12. 12 Dominant strategy Aplayers has a dominant strategy if that player's best strategy does not depend on what other players do. P1(S,T) >= P1 (S’, T) Strict Dominant strategy P1(S,T) > P1 (S’, T) Games with dominant strategies are easy to play No need for “what if …” thinking
- 13. 13 Prisoner's Dilemma Strategiesmust be undertaken without the full knowledge of what other players will do. Players adopt dominant strategies BUT they don't necessarily lead to the best outcome.
- 14. 14 Nash Equilibrium ANash equilibrium is a situation in which none of them have dominant Strategy and each player makes his or her best response (S, T) is Nash equilibrium if S is the best strategy to T and T is the best strategy to S John Nash shared the 1994 Nobel prize in Economic for developing this idea!
- 15. 15 Coordination Game Your Partner Power Point Keynote You Power Point 1,1 0, 0 Keynot e 0, 0 1, 1
- 16. 16 Other samples ofCoordination Game Using Metric units of measurement of English Units Two people trying to find each other in a crowded mall with two entrance … These games has more than one Nash Equilibrium
- 17. 17 Unbalanced Coordination Game YourPartner Power Point Keynote You Power Point 1, 1 0, 0 Keynot e 0, 0 2, 2
- 18. 18 Battle of theSexes
- 19. 19 Mixed Strategies- MatchingPennies Zero-sum Game Player 2 Head Tail Player 1 Head -1, +1 +1, -1 Tail +1, -1 -1, +1
- 20. 20 Three or MorePlayers
- 21.
- 22.