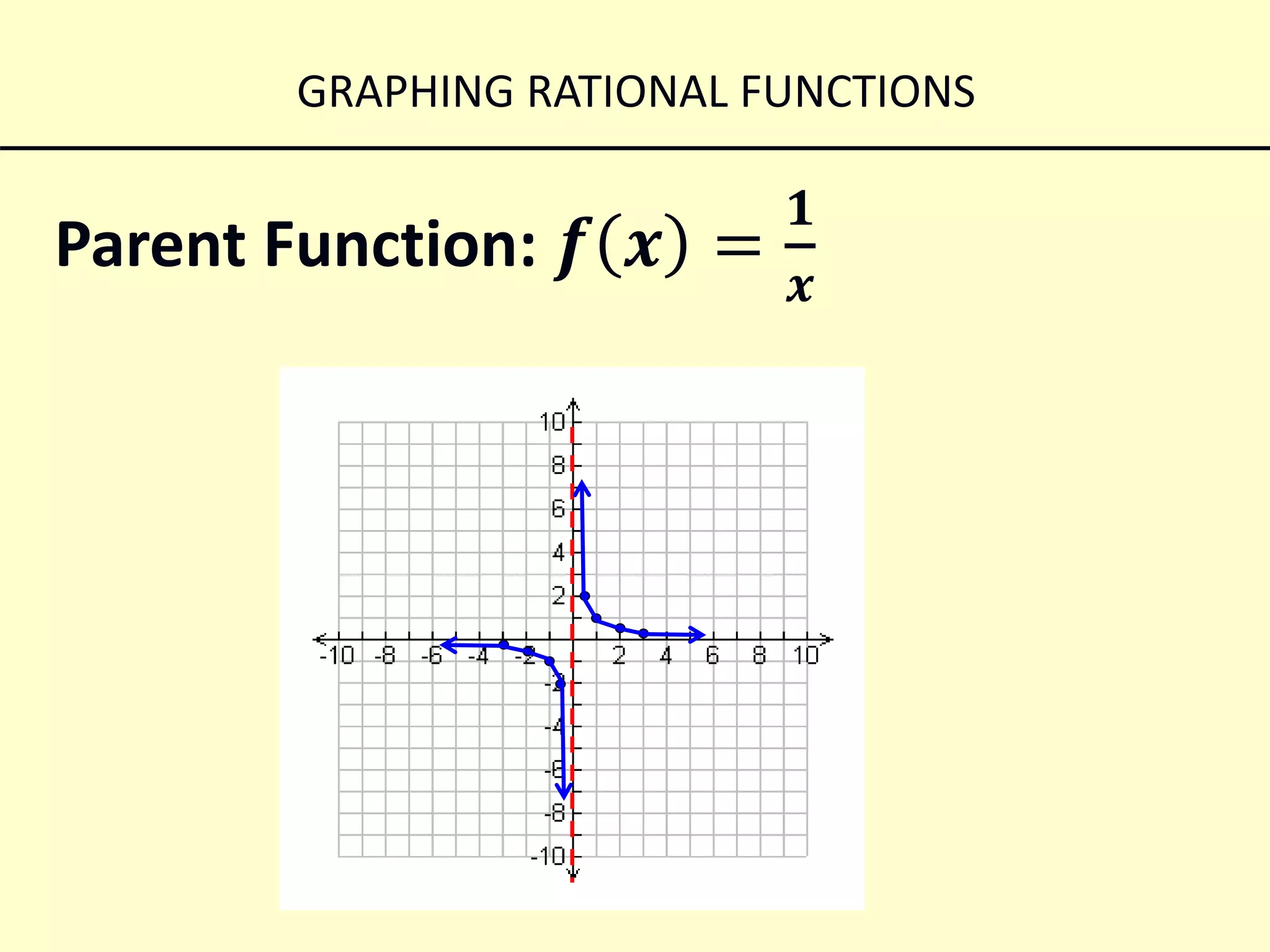
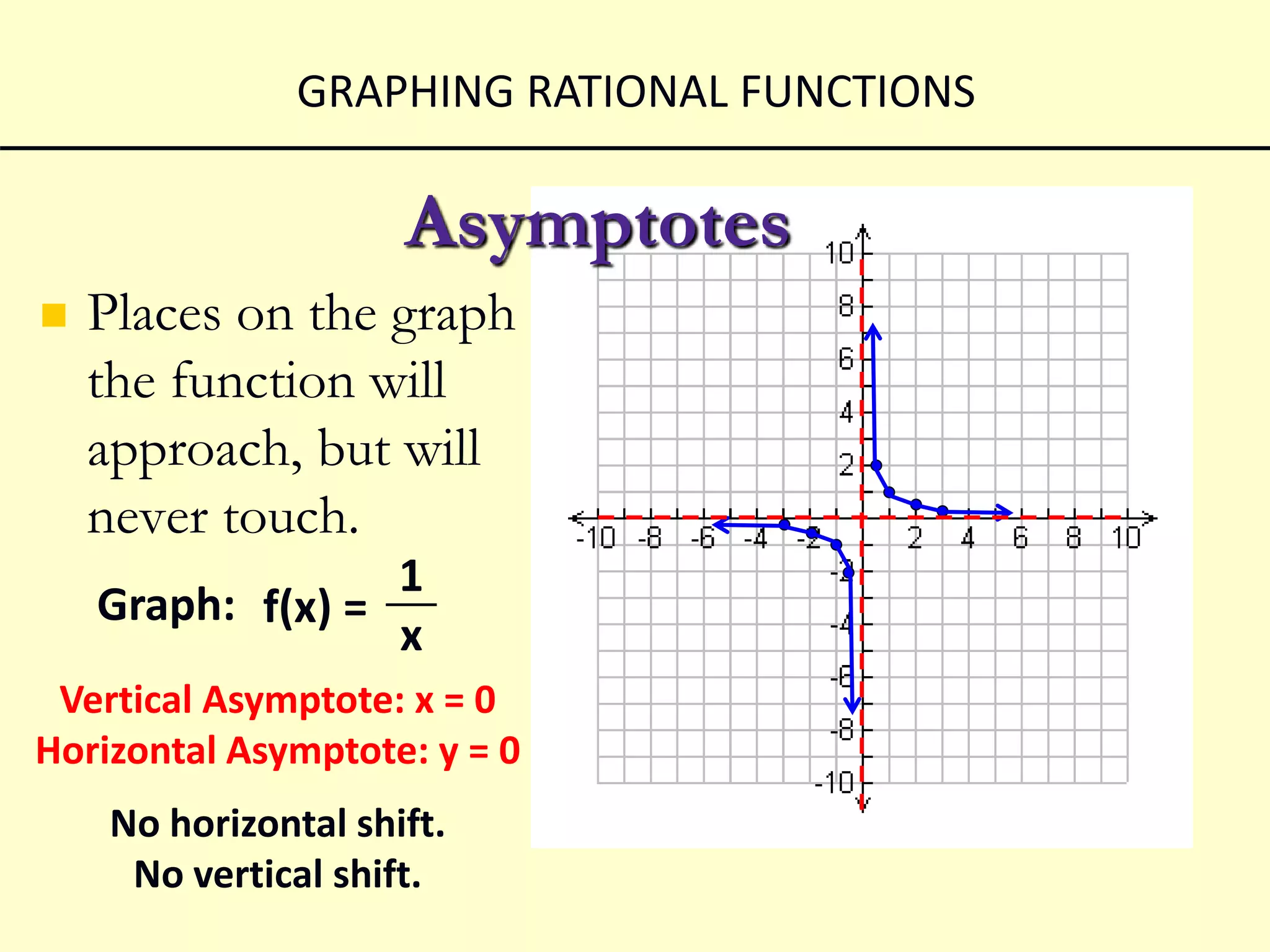
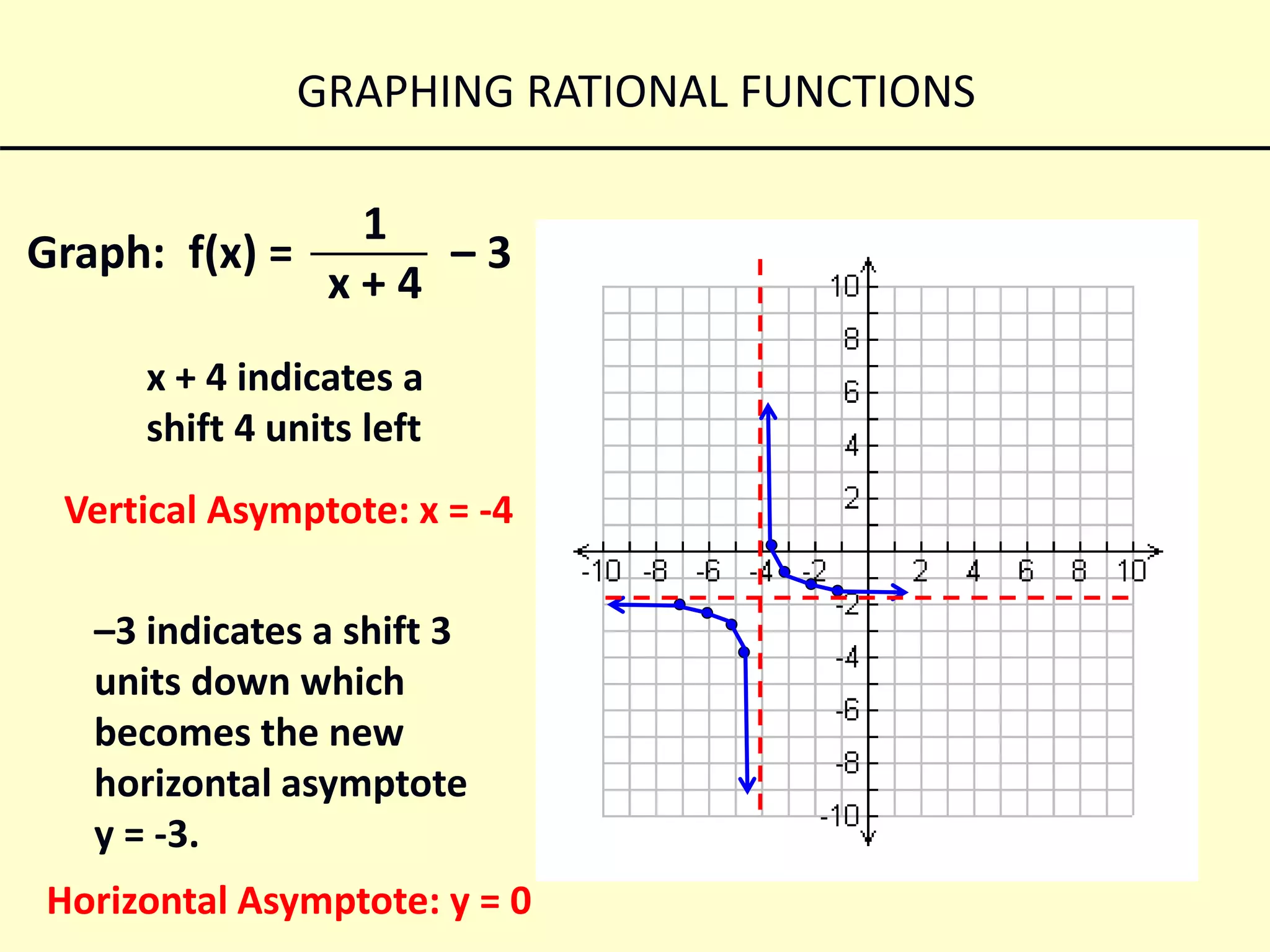
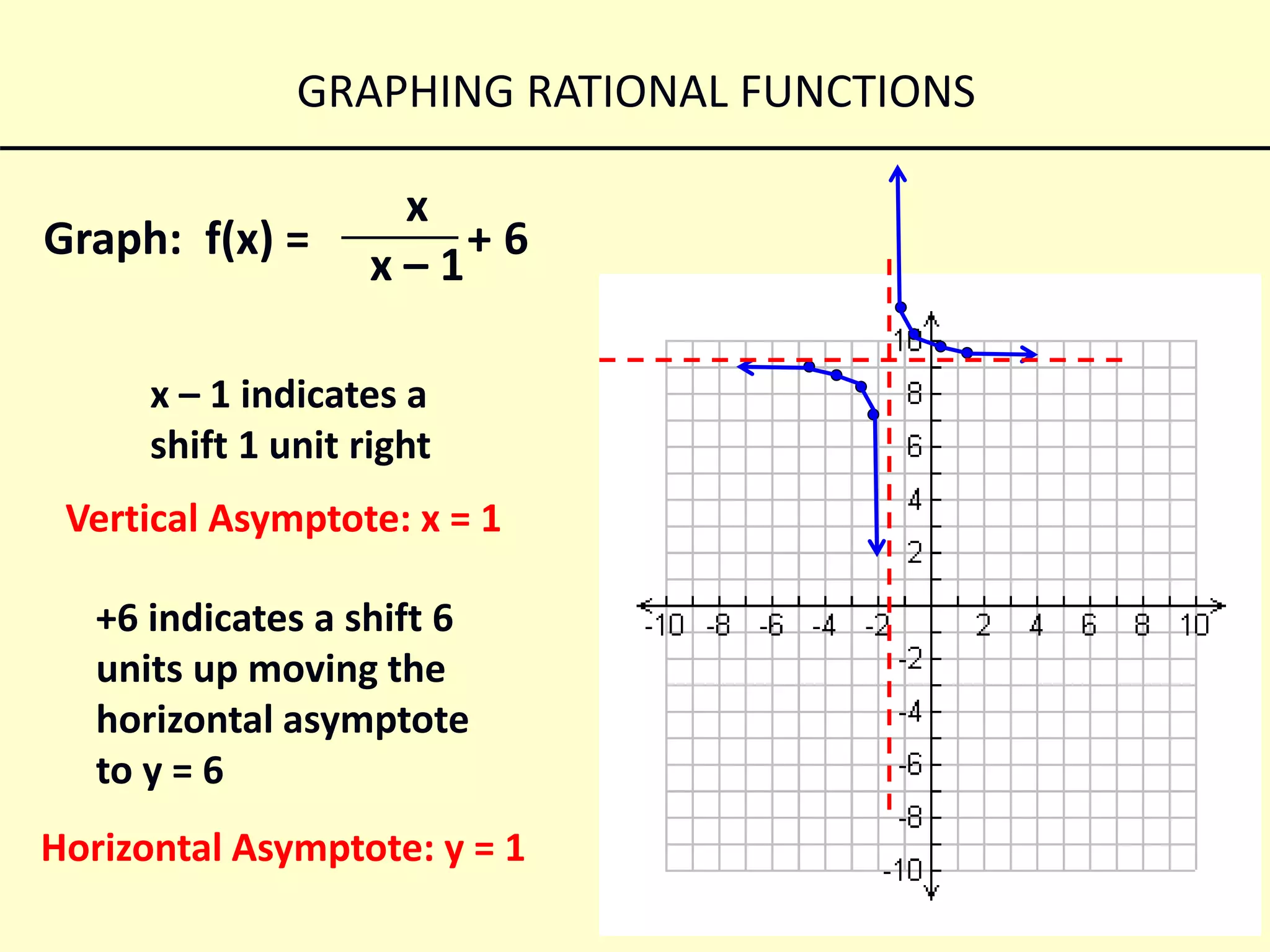
This document discusses how to graph rational functions. It explains that rational functions have vertical and horizontal asymptotes. Vertical asymptotes occur when the denominator is set equal to zero. Horizontal asymptotes depend on the degrees of the numerator and denominator. If the denominator degree is greater, the horizontal asymptote is the x-axis. If the degrees are the same, the asymptote is found by dividing the leading coefficients. If there is a vertical shift, the asymptote is the same as the shift value. Examples are provided to demonstrate graphing different rational functions based on their asymptotes.

1. GRAPHING RATIONAL FUNCTIONS
INTERVENTION MATERIAL
IN
GENERAL MATHEMATICS
FIRST SEMESTER
SY 2016-2017
Prepared by:
KRISTEL ANN G. ALDAY
Teacher III

2. GRAPHING RATIONAL FUNCTIONS
Warm Up
Graph the function
𝑓 𝑥 = − 𝑥 + 3 2
+ 4

3. GRAPHING RATIONAL FUNCTIONS
Parent Function: 𝒇 𝒙 =
𝟏
𝒙

4. GRAPHING RATIONAL FUNCTIONS
f(x) = + k
a
x – h
(-a indicates a reflection
in the x-axis)
vertical translation
(-k = down, +k = up)
horizontal translation
(+h = left, -h = right)
Pay attention to the transformation clues!
Watch the negative sign!! If
h = -2 it will appear as x + 2.

5. GRAPHING RATIONAL FUNCTIONS
Vertical Asymptote: x = 0
Horizontal Asymptote: y = 0
f(x) =
1
x
Graph:
No horizontal shift.
No vertical shift.
Asymptotes
 Places on the graph
the function will
approach, but will
never touch.

6. GRAPHING RATIONAL FUNCTIONS
W𝐡𝐚𝐭 𝐝𝐨𝐞𝐬 𝒇 𝒙 = −
𝟏
𝒙
look like?

7. GRAPHING RATIONAL FUNCTIONS
Graph: f(x) =
1
x + 4
Vertical Asymptote: x = -4
x + 4 indicates a
shift 4 units left
Horizontal Asymptote: y = 0
No vertical shift

8. GRAPHING RATIONAL FUNCTIONS
Graph: f(x) = – 3
1
x + 4
x + 4 indicates a
shift 4 units left
–3 indicates a shift 3
units down which
becomes the new
horizontal asymptote
y = -3.
Vertical Asymptote: x = -4
Horizontal Asymptote: y = 0

9. GRAPHING RATIONAL FUNCTIONS
Graph: f(x) = + 6
x
x – 1
x – 1 indicates a
shift 1 unit right
+6 indicates a shift 6
units up moving the
horizontal asymptote
to y = 6
Vertical Asymptote: x = 1
Horizontal Asymptote: y = 1

10. GRAPHING RATIONAL FUNCTIONS
You try!!
1. 𝑦 =
1
𝑥
+ 2

11. GRAPHING RATIONAL FUNCTIONS
You try!!
2. 𝑦 =
1
𝑥+3
− 4

12. GRAPHING RATIONAL FUNCTIONS
How do we find asymptotes
based on an equation only?

13. GRAPHING RATIONAL FUNCTIONS
Vertical Asymptotes (easy one)
 Set the denominator equal to zero and solve for
x.
 Example: 𝑦 =
6
𝑥−3
 x-3=0 x=3
 So: 3 is a vertical asymptote.

14. GRAPHING RATIONAL FUNCTIONS
Horizontal Asymptotes (H.A)
 In order to have a horizontal asymptote, the
degree of the denominator must be the same, or
greater than the degree in the numerator.
 Examples:
 𝑦 =
𝑥2−3
𝑥+7
No H.A because 2 > 1
 𝑦 =
𝑥3−2
𝑥3−2
Has a H.A because 3=3.
 𝑦 =
𝑥+1
𝑥2 Has a H.A because 1 < 2

15. GRAPHING RATIONAL FUNCTIONS
3 cases
to consider in determining
Horizontal Asymptote of the
graph of a Rational Function

16. GRAPHING RATIONAL FUNCTIONS
If the degree of the denominator
is GREATER than the
numerator.
 The Asymptote is y=0 ( the x-axis)

17. GRAPHING RATIONAL FUNCTIONS
If the degree of the denominator
and numerator are the same:
 Divide the leading coefficient of the numerator
by the leading coefficient of the denominator in
order to find the horizontal asymptote.
 Example: 𝑦 =
6𝑥3
3𝑥3−2
 Asymptote is 6/3 =2.

18. GRAPHING RATIONAL FUNCTIONS
If there is a Vertical Shift
 The asymptote will be the same number as the
vertical shift.
 (think about why this is based on the examples
we did with graphs)
 Example:
5
𝑥−3
+ 7
 Vertical shift is 7, so H.A is at 7.