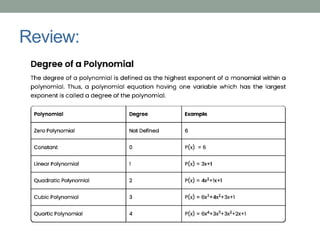
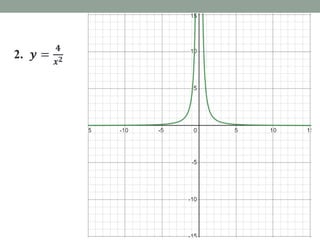
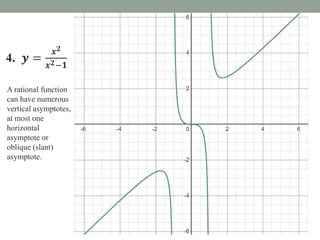
This document provides an overview of rational functions, equations, and inequalities. It discusses the domain, asymptotes, and graphing of rational functions. Procedures are outlined for solving rational equations by finding the lowest common denominator and checking solutions. Solving rational inequalities is described as finding the lowest common denominator and determining the sign of the numerator to identify the solution set. Examples are provided to illustrate key concepts and solution methods.

1. I. RATIONAL FUNCTIONS,
EQUATIONS AND
INEQUALITIES

2. Review:

3. Review:

4. Review:

5. Review:

6. Rational Functions
1. Rational Functions
a. Domain of Rational Functions
b. Asymptotes of Rational Function
c. Graphing Rational Functions
2. Solving Rational Equations
3. Solving Rational Inequalities
4. Solving Situations Involving Rational Functions,
Equations, and Inequalities

7. Rational Functions
Examples:
1. 𝑓 𝑥 =
1
𝑥
2. 𝑃 𝑥 =
2+𝑥
𝑥2
3. 𝑦 =
𝑛(3𝑛−1)
2−𝑛

8. Rational Functions
Example: Finding the Domain of Rational Functions
Find the domain of the following rational functions by
determining the values for which each denominator is zero, thus
making the rational expression undefined.
a. 𝑓 𝑥 =
2
𝑥2
b. 𝑔 𝑥 =
𝑥+1
2𝑥+1
c. 𝑦 =
3𝑥+4
𝑥2+𝑥−12

9. Rational Functions
Study the graphs of these rational functions.
1. 𝑦 =
1
𝑥
2. 𝑦 =
4
𝑥2

10. 1. 𝒚 =
𝟏
𝒙

11. 2. 𝒚 =
𝟒
𝒙𝟐

12. 1. 𝒚 =
𝟏
𝒙

13. 2. 𝒚 =
𝟒
𝒙𝟐

14. 3. 𝒚 =
𝒙−𝟏
𝒙𝟐−𝟒
A rational function
can have numerous
vertical asymptotes,
at most one
horizontal
asymptote or
oblique (slant)
asymptote.

15. 4. 𝒚 =
𝒙𝟐
𝒙𝟐−𝟏
A rational function
can have numerous
vertical asymptotes,
at most one
horizontal
asymptote or
oblique (slant)
asymptote.

16. To determine the asymptotes of a rational function
𝑓 𝑥 =
𝑃(𝑥)
𝑄(𝑥)
=
𝑎𝑛𝑥𝑛
+ 𝑎𝑛−1𝑥𝑛−1
+ … + 𝑎1 𝑥 + 𝑎0
𝑏𝑛𝑥𝑛 + 𝑏𝑛−1𝑥𝑛−1 + … + 𝑏1 𝑥 + 𝑏0
Follow these guidelines:
1. A graph has a vertical asymptote, line x=a, at each value a where the
denominator is zero.
2. The horizontal asymptote is determined using the following:
a. If n < m, then the graph has a horizontal asymptote at line y = 0.
b. If n = m, then the graph has a horizontal asymptote at line y =
𝑎𝑛
𝑏𝑛
.
c. If n > m, then the graph has no horizontal asymptote.
3. The graph of a rational function has an oblique asymptote if n = m + 1.
To determine the equation of the oblique asymptote, the numerator P(x)
is divided by the denominator Q(x) using long division. In the resulting
quotient
𝑃(𝑥)
𝑄(𝑥)
+ 𝐷 𝑥 =
𝑅(𝑥)
𝑄(𝑥)
, 𝑦 = 𝐷(𝑥) is the equation of the oblique
asymptote.

17. Determine the asymptotes (vertical, horizontal, oblique), if any, of the
given rational functions.
a. 𝑓 𝑥 =
𝑥−3
𝑥2−9
b. 𝑦 =
5𝑥−2𝑥2−3
𝑥2+4𝑥+4
c. 𝑦 =
𝑥3+2𝑥2−𝑥−2
𝑥2+1

18. Graphing a Rational Function
Follow these steps in graphing a rational function f(x):
1. Simplify the faction by factoring the numerator and
denominator, if possible.
2. Find and plot the x-intercept(s) by solving f(x) = 0.
3. Find and plot the y-intercept by evaluating f(0).
4. Determine and sketch the graph of the asymptotes.
5. Plot points between and beyond x-intercept and vertical
asymptotes to approximate the behavior of the graph in each
interval.
6. Draw smooth curves to connect the points and to sketch how
the graph behaves as the values get closer to the asymptotes.

19. Example: Graphing Rational Functions
Graph the following rational functions, then determine their domain
and range.
a. 𝑦 =
4−𝑥
2𝑥+1
b. 𝑦 =
𝑥3−2𝑥2−15𝑥
𝑥2−2𝑥

20. Rational Equations
• A rational equation is an equation involving one or more
rational expressions.
• Examples:
1.
2
𝑥−3
= 0
2.
1
𝑥
−
𝑥
𝑥+1
= 4
3.
𝑥+1
𝑥2−3𝑥+2
=
5
2𝑥

21. Solving Rational Equations
Procedure in solving rational equations:
a. Find the LCD
b. Multiply both sides by the LCD
c. Check the solutions by substitution

22. Solving Rational Equations
a. 8 −
4
𝑥
= 2 +
5
𝑥

23. Solving Rational Equations
b.
𝑥
𝑥+4
+
2
𝑥
= 1

24. Solving Rational Equations
c.
1
𝑥+2
=
6
𝑥2+𝑥−2

25. Solving Rational Equations
d.
𝑥−3
𝑥+2
−
1+𝑥
𝑥+1
=
5
𝑥

26. Rational Inequalities
• A rational inequality is an inequality involving at least one
rational expression.
• Examples:
1.
𝑥
𝑥+1
≥ 1
2.
1
𝑥
−
2
𝑥2 < 0
3.
𝑥2+2𝑥+1
𝑥−4
≤
𝑥
1−𝑥

27. Solving Rational Inequalities
Here are the steps in solving rational inequality:
1. Express the inequality in general form, that is rewrite it such
that one side of the inequality is zero.
2. Find the LCD of the

28. Solving Rational Inequalities
a.
2𝑥