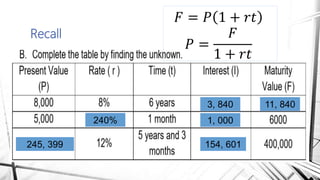
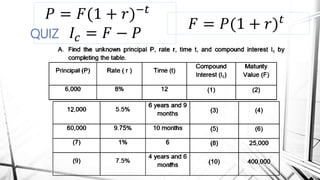
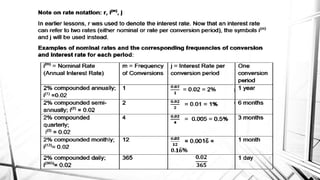
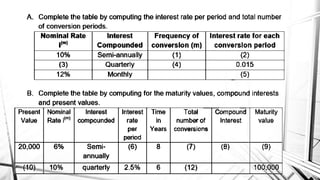
Compound interest is interest calculated on the initial principal and also on the accumulated interest from previous periods of time. More frequent compounding results in higher total interest earned over time. For example, compounding interest semi-annually instead of annually means interest is earned twice as often, leading to greater overall growth of the principal amount. The document provides examples of compound interest calculations using common formulas and variables like principal, interest rate, time period, and future/maturity value.

1. Compound Interest

2. Match Column A with Column B
RECALL
Column A Column B
1. Principal A. The time money is borrowed or invested
2. Term B. The amount paid or earned for the use of the money
3. Interest C. The percentage of increase of investment or loan
4. Maturity (Future) Value D. The amount of money borrowed or invested
5. Interest Rate E. The amount added by the lender, to be received on payment date
6. Origin F. The amount received on repayment date

3. Recall
3, 840 11, 840
1, 000240%
245, 399 154, 601
𝐹 = 𝑃 1 + 𝑟𝑡
𝑃 =
𝐹
1 + 𝑟𝑡

4. • Maturity Value
• Present Value
Goal and Objective

5. The following table shows the amount at the end of each year if principal P is
invested at an annual interest rate r compounded annually. Computations for the
particular example P = P100,000 and r = 5% are also included.
Today’s Situation

6. How Did We Get Here?

13. 𝑃 = 𝐹(1 + 𝑟)−𝑡
=50,000(1.1)-7
=50,000(0.5132)

15. Seat Work
1. Mr. Ocampo invested P150,000 at 10% compounded annually. He plans
to get this amount after 6 years for his son’s college education. How
much will he get?
2. What is the interest of P25,000 if invested at 4.5% compounded
annually in 3 years and 2 months?
3. Mr. Bautista aims to have his investment grow to P500,000 in 4 years.
How much should he invest in an account that pays 5% compounded
annually?
4. Mrs. Versoza wants to compare simple and compound interests on a
P350,000 investment for 3 and 3 months years.
a. Find the interest if funds earn 6.5% simple interest for 1 year.
b. b. Find the interest if funds earn 6.5% interest compounded annually.
c. c. Find the difference between the two interests.

21. QUIZ
𝑃 = 𝐹(1 + 𝑟)−𝑡
𝐼𝑐 = 𝐹 − 𝑃
𝐹 = 𝑃(1 + 𝑟) 𝑡

22. Solve the following problems on compound interest.
1. Peter borrowed P100,000 at 8% compounded annually. How much will he be
paying after 2 years?
2. A time deposit account in a bank yields 5.5% compound interest annually.
Jennifer invested P450,000 for 4 years in this savings account. How much
interest will she gain?
3. In order to have P250,000 in 5 years, how much should you invest if the
compound interest is 12%?
4. How much money must be invested to obtain an amount of P150,000 in 2 years
if money earns at 10.5% compounded annually?
5. What amount must be deposited by a student in a bank that pays 2 %
compounded annually so that after 12 years he will have P100,000?
𝑃 = 𝐹(1 + 𝑟)−𝑡
𝐼𝑐 = 𝐹 − 𝑃
𝐹 = 𝑃(1 + 𝑟) 𝑡

23. 1. Peter borrowed P100,000 at 8% compounded annually.
How much will he be paying after 2 years?
Given: P=100,000 r=8%=0.08 t=2 years
F=P(1+r)t=(100,000)(1+0.08)2=116, 640
2. A time deposit account in a bank yields 5.5% compound
interest annually. Jennifer invested P450,000 for 4 years
in this savings account. How much interest will she
gain?
Given: P=450,000 r=5.5%=0.055 t=4 years
F=P(1+r)t=(450,000)(1+0.055)4=557, 471.0928
Ic=F-P=557, 471.0928-450, 000=107, 471.0928

24. 3. In order to have P250,000 in 5 years, how much
should you invest if the compound interest is 12%?
Given: F=250,000 r=12%=0.12 t=5 years
P=F(1+r)-t=(250,000)(1+0.12)-5=141, 856.7139
4. How much money must be invested to obtain an
amount of P150,000 in 2 years if money earns at 10.5%
compounded annually?
Given: F=150,000 r=10.5%=0.105 t=2 years
P=F(1+r)-t =(150,000)(1+0.105)-2=122, 847.6075

25. 5. What amount must be deposited by a student in a
bank that pays 2 % compounded annually so that after
12 years he will have P100,000?
Given: F=100,000 r=2%=0.02 t=12 years
P=F(1+r)-t =(100,000)(1+0.02)-12=78, 849. 31756

26. Compounding more than
once a year

27. Example 1. Given a principal of PhP 10,000, which of the following options
will yield greater interest after 5 years: OPTION A: Earn an annual interest
rate of 2% at the end of the year, or OPTION B: Earn an annual interest rate
of 2% in two portions—1% after 6 months, and 1% after another 6 months?
Solution.
Sometimes, interest may be
compounded more than once a year.

28. Answer: Option B
will give the higher
interest after 5
years. If all else is
equal, a more
frequent
compounding will
result in a higher
interest, which is
why Option B gives
a higher interest
than Option A.

29. The investment scheme in Option B introduces new concepts because
interest is compounded twice a year, the conversion period is 6 months,
and the frequency of conversion is 2. As the investment runs for 5 years,
the total number of conversion periods is 10. The nominal rate is 2% and
the rate of interest for each conversion period is 1%.
Definition of Terms:
Frequency of conversion (m) – number of conversion periods in one year
Conversion or interest period– time between successive conversions of
interest
Total number of conversion periods n
n = mt = (frequency of conversion)x(time in years)
Nominal rate (i(m)) – annual rate of interest
Rate (j) of interest for each conversion period

32. 𝑗 =
𝑖(𝑚)
𝑚
𝑛 = 𝑚𝑡
F = P(1 + 𝑗) 𝑛

33. IC

36. 𝑗 =
𝑖(𝑚)
𝑚
𝑛 = 𝑚𝑡
P =
𝐹
(1 + 𝑗) 𝑛
P = 𝐹(1 + 𝑗)−𝑛

37. P = 𝐹(1 + 𝑗)−𝑛
P=(25,000)(1+0.025)-10=19, 529.96

38. m=2
m=4
m=12