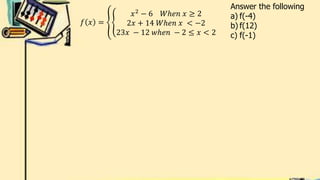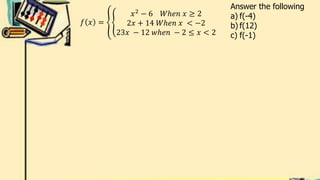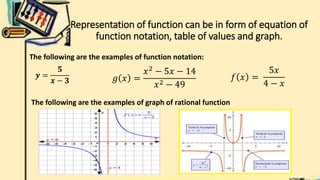
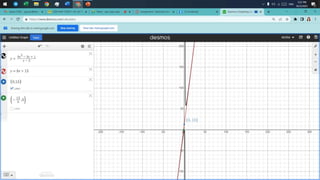
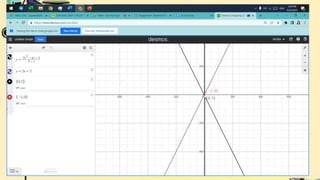
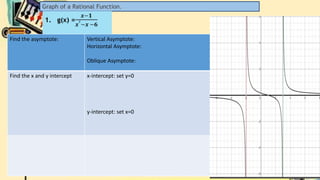
This document discusses various topics related to piecewise functions and rational functions: - It defines piecewise functions and provides examples of evaluating piecewise functions at given values. - It introduces rational functions as functions of the form p(x)/q(x) where p(x) and q(x) are polynomials and q(x) is not equal to zero. It discusses representing rational functions in different forms. 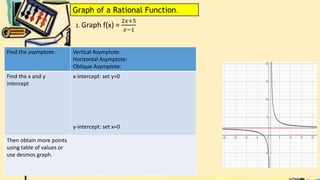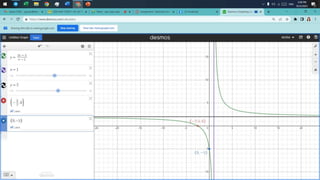- It explains how to identify restrictions or extraneous roots of rational functions by setting the denominator equal to zero. It also discusses how to determine the domain of a rational function based on its restrictions. 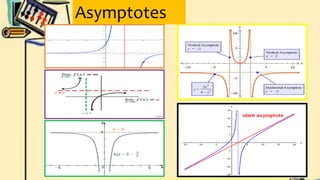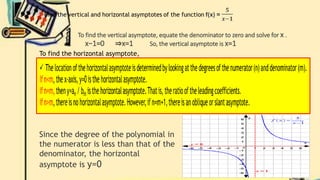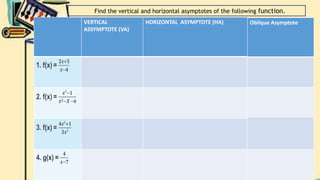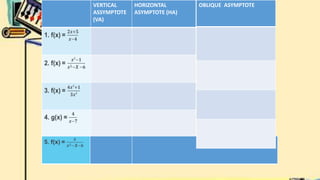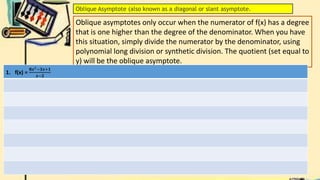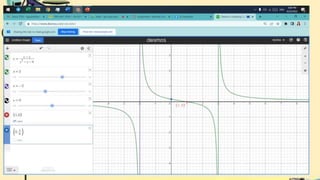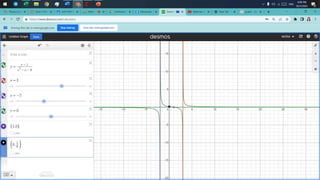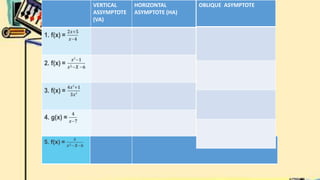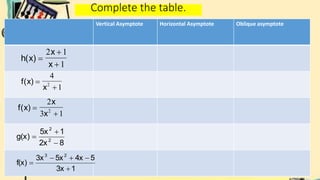- Finally, it defines vertical and horizontal asymptotes of rational functions. It provides

1. General Mathematics
Topics that we need to discuss for today.
- Evaluation of Piece – Wise functions
-Rational Function
- Restrictions/Extraneous roots
- Domain of Rational Function
- Asymptotes
- Intercepts

2. Piecewise Function
A piecewise function is a function built from
pieces of different functions over different intervals
𝒇 𝒙 =
𝒙𝟐
− 𝟔 𝑾𝒉𝒆𝒏 𝒙 ≥ 𝟐
𝟐𝒙 + 𝟏𝟒 𝑾𝒉𝒆𝒏 𝒙 < −𝟐
𝟐𝟑𝒙 − 𝟏𝟐 𝒘𝒉𝒆𝒏 − 𝟐 ≤ 𝒙 < 𝟐
Evaluating Piecewise Function
𝒇 𝒙 =
𝒙𝟐
− 𝟐𝒙 + 𝟏 𝒘𝒉𝒆𝒏 𝒙 ≥ 𝟒
𝟏𝟐𝒙 − 𝟐𝟑 𝒘𝒉𝒆𝒏 𝒙 < −𝟒
𝟓𝒙 − 𝟏𝟐 𝒘𝒉𝒆𝒏 − 𝟒 ≤ 𝒙 < 𝟒
Answer the following
a) f(-4)
b) f(12)
c) f(-1)
𝐴𝑛𝑠𝑤𝑒𝑟 𝑡ℎ𝑒 𝑓𝑜𝑙𝑙𝑜𝑤𝑖𝑛𝑔:
a) f(-5)
b) f(2)
c) f(5)

3. Evaluating Piecewise Functions:
Evaluating piecewise functions is just like
evaluating functions that you are already familiar
with.
f(x) = x2 + 1 , x  0
x – 1 , x  0
Let’s calculate f(2).
You are being asked to find y when
x = 2. Since 2 is  0, you will only
substitute into the second part of the
function.
f(2) = 2 – 1 = 1

4. f(x) = x2 + 1 , x  0
x – 1 , x  0
Let’s calculate f(-
2). use
You are being asked to find y when
x = -2. Since -2 is  0, you will only substitute into the
first part of the function.
f(-2) = x² + 1
= (-2)2 + 1
= 5

5. Answer the following
a) f(-4)
b) f(12)
c) f(-1)
𝑓 𝑥 =
𝑥2 − 6 𝑊ℎ𝑒𝑛 𝑥 ≥ 2
2𝑥 + 14 𝑊ℎ𝑒𝑛 𝑥 < −2
23𝑥 − 12 𝑤ℎ𝑒𝑛 − 2 ≤ 𝑥 < 2

6. Answer the following
a) f(-4)
b) f(12)
c) f(-1)
𝑓 𝑥 =
𝑥2 − 6 𝑊ℎ𝑒𝑛 𝑥 ≥ 2
2𝑥 + 14 𝑊ℎ𝑒𝑛 𝑥 < −2
23𝑥 − 12 𝑤ℎ𝑒𝑛 − 2 ≤ 𝑥 < 2

7. 𝑓 𝑥 =
𝑥2 − 2𝑥 + 1 𝑤ℎ𝑒𝑛 𝑥 ≥ 4
12𝑥 − 23 𝑤ℎ𝑒𝑛 𝑥 < −4
5𝑥 − 12 𝑤ℎ𝑒𝑛 − 4 ≤ 𝑥 < 4
𝐴𝑛𝑠𝑤𝑒𝑟 𝑡ℎ𝑒 𝑓𝑜𝑙𝑙𝑜𝑤𝑖𝑛𝑔:
a) f(-5)
b) f(2)
c) f(8)

8. A rational expression is an expression of the
form
𝒑
𝒒
where p and q are polynomials and q(x)≠0.
Similarly, we define a rational function as a function of the form
𝐑 𝒙 =
𝒑(𝒙)
𝒒(𝒙)
where p(x) and q(x) are both polynomials and q(x) is not equal to
zero.
Rational Function

9. Representation of function can be in form of equation of
function notation, table of values and graph.
𝒚 =
𝟓
𝒙 − 𝟑 𝑓 𝑥 =
5𝑥
4 − 𝑥
𝑔 𝑥 =
𝑥2 − 5𝑥 − 14
𝑥2 − 49
The following are the examples of function notation:
The following are the examples of graph of rational function

10. Identifying Restrictions and Simplifying Rational
Functions
Restrictions or extraneous roots are the real numbers for
which the functions are not defined. The domain of a rational
function in terms of its restrictions must be determined.
𝑓 𝑥 =
𝑥2
− 6𝑥 + 9
𝑥2 + 3𝑥 − 18
Example 1:
𝑓 𝑥 =
(𝑥 − 3)(𝑥 − 3)
(𝑥 − 3)(𝑥 + 6)
𝑓 𝑥 =
𝑥 − 3
𝑥 + 6
𝑅𝑒𝑠𝑡𝑟𝑖𝑐𝑡𝑖𝑜𝑛𝑠:
𝑥 − 3 𝑥 + 6 = 0 → 𝐷𝑒𝑛𝑜𝑚𝑖𝑛𝑎𝑡𝑜𝑟
𝑥 − 3 = 0 𝑜𝑟 𝑥 + 6 = 0
𝑥 = 3 𝑥 = −6

11. Identifying Restrictions and Simplifying Rational
Functions
Restrictions or extraneous roots are the real numbers for
which the functions are not defined. The domain of a rational
function in terms of its restrictions must be determined.
𝑓 𝑥 =
𝑥2
− 6𝑥 + 9
𝑥2 + 3𝑥 − 18
Example 1:
𝑓 𝑥 =
(𝑥 − 3)(𝑥 − 3)
(𝑥 − 3)(𝑥 + 6)
𝑓 𝑥 =
𝑥 − 3
𝑥 + 6
𝑅𝑒𝑠𝑡𝑟𝑖𝑐𝑡𝑖𝑜𝑛𝑠:
𝑥 − 3 𝑥 + 6 = 0 → 𝐷𝑒𝑛𝑜𝑚𝑖𝑛𝑎𝑡𝑜𝑟
𝑥 − 3 = 0 𝑜𝑟 𝑥 + 6 = 0
𝑥 = 3 𝑥 = −6
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝒕𝒉𝒆 𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝒇𝒖𝒏𝒄𝒕𝒊𝒐𝒏 𝒊𝒔 𝒅𝒆𝒇𝒊𝒏𝒆𝒅
𝒇𝒐𝒓 𝒂𝒏𝒚 𝒓𝒆𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓𝒔 𝒆𝒙𝒄𝒆𝒑𝒕 𝟑 𝒂𝒏𝒅 − 𝟔.
𝒙𝒍𝒙 ≠ −𝟔, 𝟑 → 𝑺𝒆𝒕 𝑩𝒖𝒊𝒍𝒅𝒆𝒓
−∞, −𝟔 𝑼 −𝟔, 𝟑 𝑼(𝟑, ∞)  Interval Notation

12. Example 2:
Determine the restriction then simplify.
p 𝑥 =
𝑥2
− 14𝑥 − 51
𝑥2 − 𝑥 − 12
𝑝 𝑥 =
(𝑥 − 17)(𝑥 + 3)
(𝑥 + 3)(𝑥 − 4)
𝑝 𝑥 =
𝑥 − 17
𝑥 − 4
Restrictions:
(𝑥 + 3) (x -4) = 0
𝑥 + 3 = 0, 𝑥 − 4 = 0
𝒙 = −𝟑, 𝒙 = 𝟒
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝒕𝒉𝒆 𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝒇𝒖𝒏𝒄𝒕𝒊𝒐𝒏 𝒊𝒔 𝒅𝒆𝒇𝒊𝒏𝒆𝒅
𝒇𝒐𝒓 𝒂𝒏𝒚 𝒓𝒆𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓𝒔 𝒆𝒙𝒄𝒆𝒑𝒕 − 𝟑 𝒂𝒏𝒅 𝟒.
𝒙𝒍𝒙 ≠ −𝟑, 𝟒 → 𝑺𝒆𝒕 𝑩𝒖𝒊𝒍𝒅𝒆𝒓
−∞, −𝟑 𝑼 −𝟑, 𝟒 𝑼(𝟒, ∞)  Interval Notation

15. Domain of a Rational Function
For rational function, there are restricted values of the domain
that will result to undefined values of range. To find the set
notation for domain, the denominator can be assigned as
function and solve for x so that the restricted values shall be
determined.
2.) g(x)=
𝟔𝒙−𝟖
𝒙𝟐−𝟒𝒙−𝟐𝟏
𝟑. ) 𝒉 𝒙 =
𝟐𝒙 − 𝟏𝟒
𝒙𝟐 − 𝟗
1.) 𝒇 𝒙 =
𝟐𝒙−𝟕
𝒙+𝟔

16. Domain of a Rational Function
For rational function, there are restricted values of the domain
that will result to undefined values of range. To find the set
notation for domain, the denominator can be assigned as
function and solve for x so that the restricted values shall be
determined.
2.) g(x)=
𝟔𝒙−𝟖
𝒙𝟐−𝟒𝒙−𝟐𝟏
𝟑. ) 𝒉 𝒙 =
𝟐𝒙 − 𝟏𝟒
𝒙𝟐 − 𝟗
1.) 𝒇 𝒙 =
𝟐𝒙−𝟕
𝒙+𝟔

17. Domain of a Rational Function
For rational function, there are restricted values of the domain
that will result to undefined values of range. To find the set
notation for domain, the denominator can be assigned as
function and solve for x so that the restricted values shall be
determined.
2.) g(x)=
𝟔𝒙−𝟖
𝒙𝟐−𝟒𝒙−𝟐𝟏
𝟑. ) 𝒉 𝒙 =
𝟐𝒙 − 𝟏𝟒
𝒙𝟐 − 𝟗
1.) 𝒇 𝒙 =
𝟐𝒙−𝟕
𝒙+𝟔

18. Asymptotes

19. Asymptotes
The asymptote of the rational function is a line or curve that the
graph of a function gets closer but does not touch the x- axis.
There are different types of asymptotes:
1. 𝑽𝒆𝒓𝒕𝒊𝒄𝒂𝒍 𝑨𝒔𝒚𝒎𝒑𝒕𝒐𝒕𝒆𝒔
- The rational function has vertical asymptote represented by the equation x =a.
-Vertical asymptote are the extraneous points of the domain of a reduced
rational function.
The values of a is the denominator of the rational function.
-to find, set a or equate the denominator to zero = o or
equate to 0, then solve the variable.
-The line x=a is a vertical asymptote for the graph of a
function f if f(x) ∞ or f(x) ∞ .
f(x) =
𝟓
𝒙−𝟑
VERTICAL ASYMPTOTE

20. Asymptotes
The asymptote of the rational function is a line or curve tht the graph of a
function gets closer but does not touch the x- axis.
There are different types of asymptotes:
𝟐. 𝑯𝒐𝒓𝒊𝒛𝒐𝒏𝒕𝒂𝒍 𝑨𝒔𝒚𝒎𝒑𝒕𝒐𝒕𝒆𝒔
The line y = b is a horizontal asymptote for the graph of f(x), if f(x) get close b as gets as very large
or very small. There are 2 cases I terms of horizontal asymptotes:
Case 1:
If the degree of the numerator of f(x) is less than the degree of the denominator then y = 0.
Case 2:
If the degree of the numerator and denominator are equal then, it divide the numeral coefficient
of both numerator and denominator.

21. Finding Horizontal Asymptotes
𝑓 𝑥 =
𝑁(𝑥)
𝐷(𝑥)
=
𝑎𝑛𝑋𝑛
+ ⋯ + 𝑎𝑛
𝑏𝑛𝑋𝑚 + ⋯ + 𝑏𝑛
a) If n > m, then horizontal asymptotes is ONE.
b)If n <m, then horizontal asymptotes is equal to 0 or y = 0.
c) If n = m , then horizontal asymptotes, y =
𝑎𝑛
𝑏𝑛

22. To find the vertical asymptote, equate the denominator to zero and solve for x .
x−1=0 ⇒x=1 So, the vertical asymptote is x=1
To find the horizontal asymptote,
Since the degree of the polynomial in
the numerator is less than that of the
denominator, the horizontal
asymptote is y=0

23. To find the vertical asymptote, equate the denominator to zero and solve for x .
x+4=0 ⇒x=-4 So, the vertical asymptote is x=-4

24. To find the vertical asymptote, equate the denominator to zero and solve for x .
x- 2 =0 ⇒x= 2 So, the vertical asymptote is x= 2
To find the horizontal asymptote,
Since the degree of the polynomial in the numerator is 3 and the degree of
the polynomial in the denominator is 1 or n>m , there is no horizontal
asymptote.

25. Find the vertical and horizontal asymptotes of the following function.
VERTICAL
ASSYMPTOTE (VA)
HORIZONTAL ASYMPTOTE (HA) Oblique Asymptote

26. Find the vertical and horizontal asymptotes of the following function.

27. for our activity today… use
Canvas RATIONAL FUNCTION
(20 POINTS)

28. VERTICAL
ASSYMPTOTE
(VA)
HORIZONTAL
ASYMPTOTE (HA)
OBLIQUE ASYMPTOTE

29. 3. Oblique Asymptote(diagonal or slant)
If the numerator is one degree greater than the
denominator, the graph has a slant asymptote. Using
polynomial division, divide the numerator by the
denominator to determine the line of the slant
asymptote.

30. Oblique Asymptote (also known as a diagonal or slant asymptote.
Oblique asymptotes only occur when the numerator of f(x) has a degree
that is one higher than the degree of the denominator. When you have
this situation, simply divide the numerator by the denominator, using
polynomial long division or synthetic division. The quotient (set equal to
y) will be the oblique asymptote.
1. f(x) =
𝟖𝒙2−𝟑𝒙+𝟏
𝒙−𝟐

31. Oblique Asymptote (also known as a diagonal or slant asymptote.
Oblique asymptotes only occur when the numerator of f(x) has a degree
that is one higher than the degree of the denominator. When you have
this situation, simply divide the numerator by the denominator, using
polynomial long division or synthetic division. The quotient (set equal to
y) will be the oblique asymptote.
1. f(x) =
𝟖𝒙2−𝟑𝒙+𝟏
𝒙−𝟐

32. Oblique Asymptote (also known as a diagonal or slant asymptote.
2. f(x) =
𝟐𝒙2−𝟒𝒙+𝟓
𝟑−𝒙

34. *Reduce the rational function to its lowest terms.
*When numerator and denominator have factor(s) in common there is a “hole” at
the zero(s).
*Arrange both the numerator and denominator in descending order by degree.
Vertical Asymptote: set denominator to zero. There may be 1, two or more or
none.
Determining Asymptote of Rational Function
There may be no vertical, horizontal or oblique asymptote. A function cannot have
both horizontal and oblique asymptote.

35. Rational Function that has a Common
Factor

36. Graph of a Rational Function.
Find the asymptote: Vertical Asymptote:
Horizontal Asymptote:
Oblique Asymptote:
Find the x and y
intercept
x-intercept: set y=0
y-intercept: set x=0
Then obtain more points
using table of values or
use desmos graph.
1. Graph f(x) =
2𝑥+5
𝑥−1

38. Graph of a Rational Function.
Find the asymptote: Vertical Asymptote:
Horizontal Asymptote:
Oblique Asymptote:
Find the x and y intercept x-intercept: set y=0
y-intercept: set x=0

41. Determine the vertical, horizontal or oblique asymptotes in each
item.
𝑓 𝑥 =
𝑥 + 1
𝑥2 − 4
𝑔 𝑥 =
10𝑥 − 24
5𝑥 − 25
ℎ 𝑥 =
𝑥2
− 2𝑥 + 1
𝑥 − 4

42. Practice!!
Given a function, f x =
𝑥+4
𝑥2−9
, Answer the following
a) Domain of the function.
b) Intercepts
c) Vertical Asymptotes
d) Horizontal or Oblique Asymptotes
e) Graph

43. Intercepts
Examine where the function crosses the x-axis and the y-axis by
solving y =f(x) = 0 and computing f(0) or x = 0
𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑒 𝑡ℎ𝑒 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑓𝑜𝑙𝑙𝑜𝑤𝑖𝑛𝑔:
𝑓 𝑥 =
𝑥 + 1
𝑥2 − 4 𝑔 𝑥 =
10𝑥 − 24
5𝑥 − 25 ℎ 𝑥 =
𝑥2
− 2𝑥 + 1
𝑥 − 4

44. VERTICAL
ASSYMPTOTE
(VA)
HORIZONTAL
ASYMPTOTE (HA)
OBLIQUE ASYMPTOTE

45. Complete the table.
Vertical Asymptote Horizontal Asymptote Oblique asymptote
h x
x
x
( ) 


2 1
1
f x
x
( ) 

4
1
2
f x
x
x
( ) 

2
3 1
2
8
2x
1
5x
g(x) 2
2



1
3x
5
4x
5x
3x
f(x)
2
3






46. Inverse Function slide