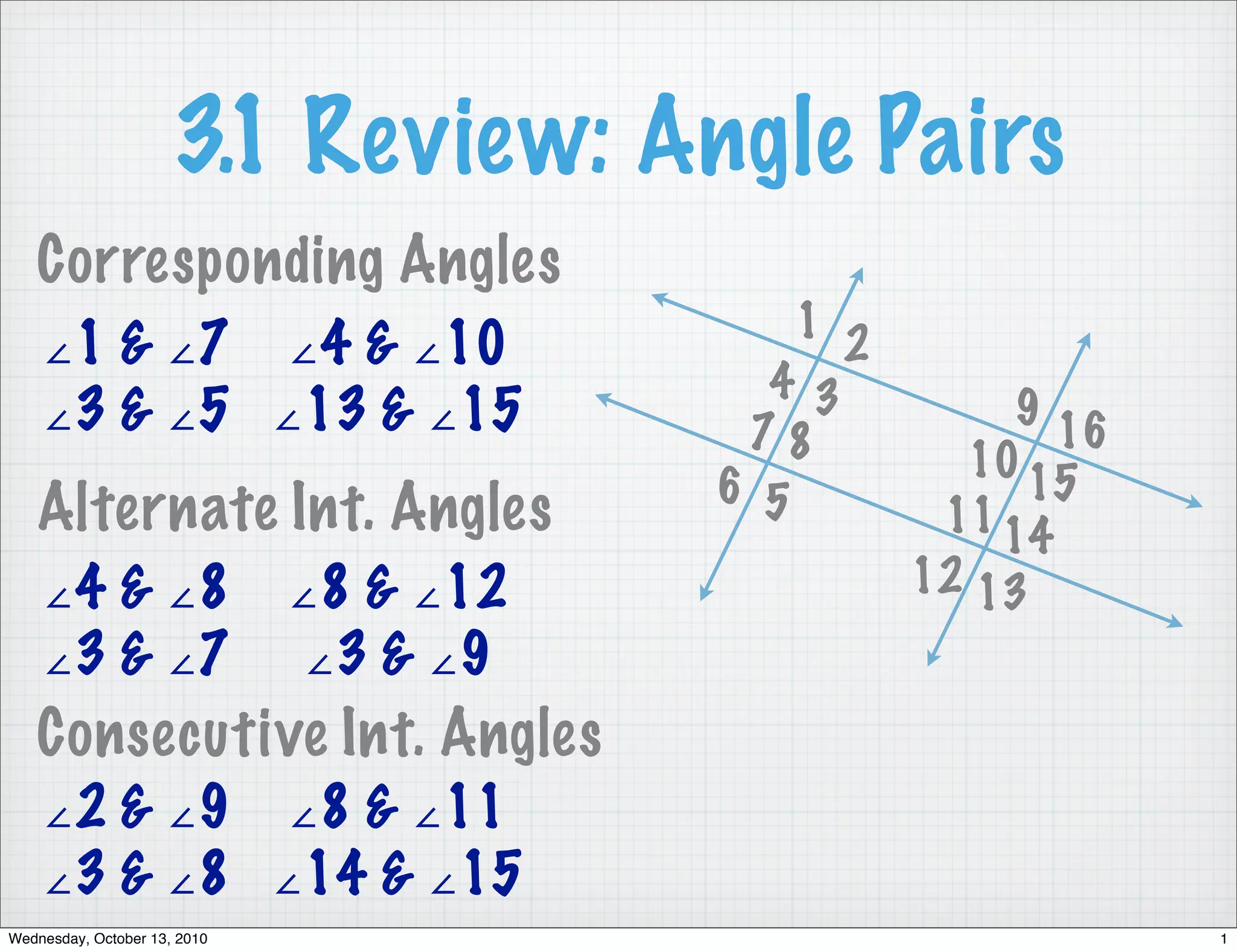
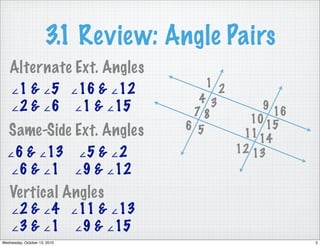
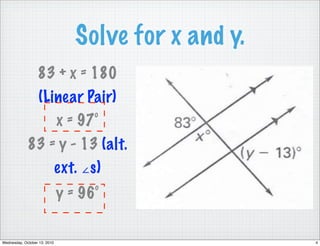
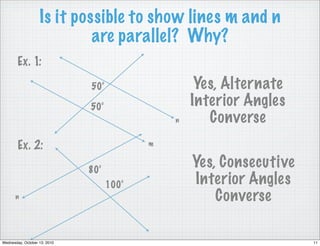
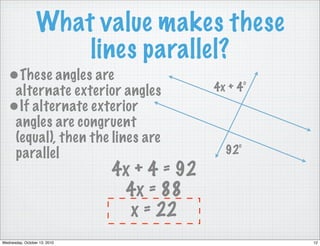
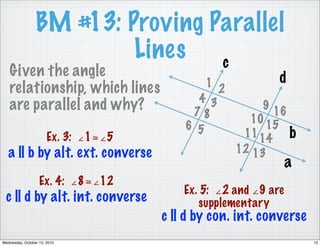
This document reviews different angle pairs that are formed when two lines intersect or are parallel, including corresponding angles, alternate interior angles, consecutive interior angles, alternate exterior angles, and vertical angles. It provides examples of using these angle relationships to determine if lines are parallel or to find the measure of unknown angles. The last pages discuss writing the converses of the angle theorems and using congruent or supplementary angles to prove that two lines are parallel. Students are assigned problems applying these concepts for homework.

1. 3.1 Review: Angle Pairs
Corresponding Angles
1 2
∠1 & ∠7 ∠4 & ∠10
4 3
∠3 & ∠5 ∠13 & ∠15 78
9 16
10 15
6 5
Alternate Int. Angles 11 14
∠4 & ∠8 ∠8 & ∠12 12 13
∠3 & ∠7 ∠3 & ∠9
Consecutive Int. Angles
∠2 & ∠9 ∠8 & ∠11
∠3 & ∠8 ∠14 & ∠15
Wednesday, October 13, 2010 1

2. 3.1 Review: Angle Pairs
Alternate Ext. Angles
1 2
∠1 & ∠5 ∠16 & ∠12
4 3
∠2 & ∠6 ∠1 & ∠15 78
9 16
10 15
Same-Side Ext. Angles 6 5
11 14
∠6 & ∠13 ∠5 & ∠2 12 13
∠6 & ∠1 ∠9 & ∠12
Vertical Angles
∠2 & ∠4 ∠11 & ∠13
∠3 & ∠1 ∠9 & ∠15
Wednesday, October 13, 2010 2

3. Solve for the missing angles.
BM 14 and 15
∠1= 127° (linear with 53°)
∠2=53° (vertical with 53°)
∠3=127° (vertical with ∠1)
∠5=53° (corr. with 53°)
∠4=37° (comp. with ∠5)
∠6=90° (vertical with rt. ∠)
∠7=37° (corr. with ∠4)
∠8=143° (linear with ∠7)
∠9=37° (vertical with ∠7)
∠10=143° (vertical with ∠8)
Wednesday, October 13, 2010 3

4. Solve for x and y.
83 + x = 180
(Linear Pair)
x = 97°
83 = y - 13 (alt.
ext. ∠s)
y = 96°
Wednesday, October 13, 2010 4

5. BM 16!!
Prove the Alternate Exterior Angles Theorem
Given: m || l Prove: ∠1 ≅ ∠2
Statements Reasons 1
1. m || l 1. Given 2 3
l
2. ∠1 ≅ ∠3 2. Corr. ∠s are ≅ m
3. ∠3 ≅ ∠2 3. Vertical ∠s are ≅
4. ∠1 ≅ ∠2 4. Transitive
Wednesday, October 13, 2010 5

6. 3.4 Proving Lines are
Parallel
Benchmark 17
Wednesday, October 13, 2010 6

7. What are Proofs?
A “step-by-step” justification
of what you are doing.
Start with the given.
Define what you know.
(Statement, then Reason)
End with your desired
conclusion.
Wednesday, October 13, 2010 7

8. Write the converse:
If t wo lines are parallel, then
their corresponding angles are
congruent.
Corresponding Angles
Converse Postulate
If t wo lines have corresponding
angles congruent, then the lines
are parallel.
Wednesday, October 13, 2010 8

9. Write the converse:
If t wo lines are parallel, then
their alternate interior angles
are congruent.
Alternate Interior Angles
Converse Theorem
If t wo lines have alternate
interior angles congruent, then
the lines are parallel.
Wednesday, October 13, 2010 9

10. Write the converse:
If t wo lines are parallel, then
their consecutive interior
angles are supplementary.
Consecutive Interior Angles
Converse Theorem
If t wo lines have consecutive
interior angles supplementary,
then the lines are parallel.
Wednesday, October 13, 2010 10

11. Is it possible to show lines m and n
are parallel? Why?
Ex. 1:
50° Yes, Alternate
50° Interior Angles
n Converse
Ex. 2: m
80°
Yes, Consecutive
100° Interior Angles
n Converse
Wednesday, October 13, 2010 11

12. What value makes these
lines parallel?
•These angles are
alternate exterior angles 4x + 4°
•If alternate exterior
angles are congruent
(equal), then the lines are
parallel 92°
4x + 4 = 92
4x = 88
x = 22
Wednesday, October 13, 2010 12

13. BM #13: Proving Parallel
Lines c
Given the angle d
relationship, which lines 1
2
4 3
are parallel and why? 78
9
16
10
6 5 15
Ex. 3: ∠1≅∠5 11 14 b
a || b by alt. ext. converse 12 13
a
Ex. 4: ∠8≅∠12
Ex. 5: ∠2 and ∠9 are
c || d by alt. int. converse supplementary
c || d by con. int. converse
Wednesday, October 13, 2010 13

14. Summary:
The Angle Theorems state “If lines
are parallel, then angles are ≅ or
supplementary.”
The Converse Theorems state “If
angles are ≅ or supplementary,
then the lines are parallel.”
Wednesday, October 13, 2010 14

15. Assignment:
#18 3-2 WS p. 295 (Due at
the end of class)
#19 p. 137 ##1-9 (odd),
10-20 (all), 26, 27, 30, 51,
52, 56-62 (even)
Wednesday, October 13, 2010 15