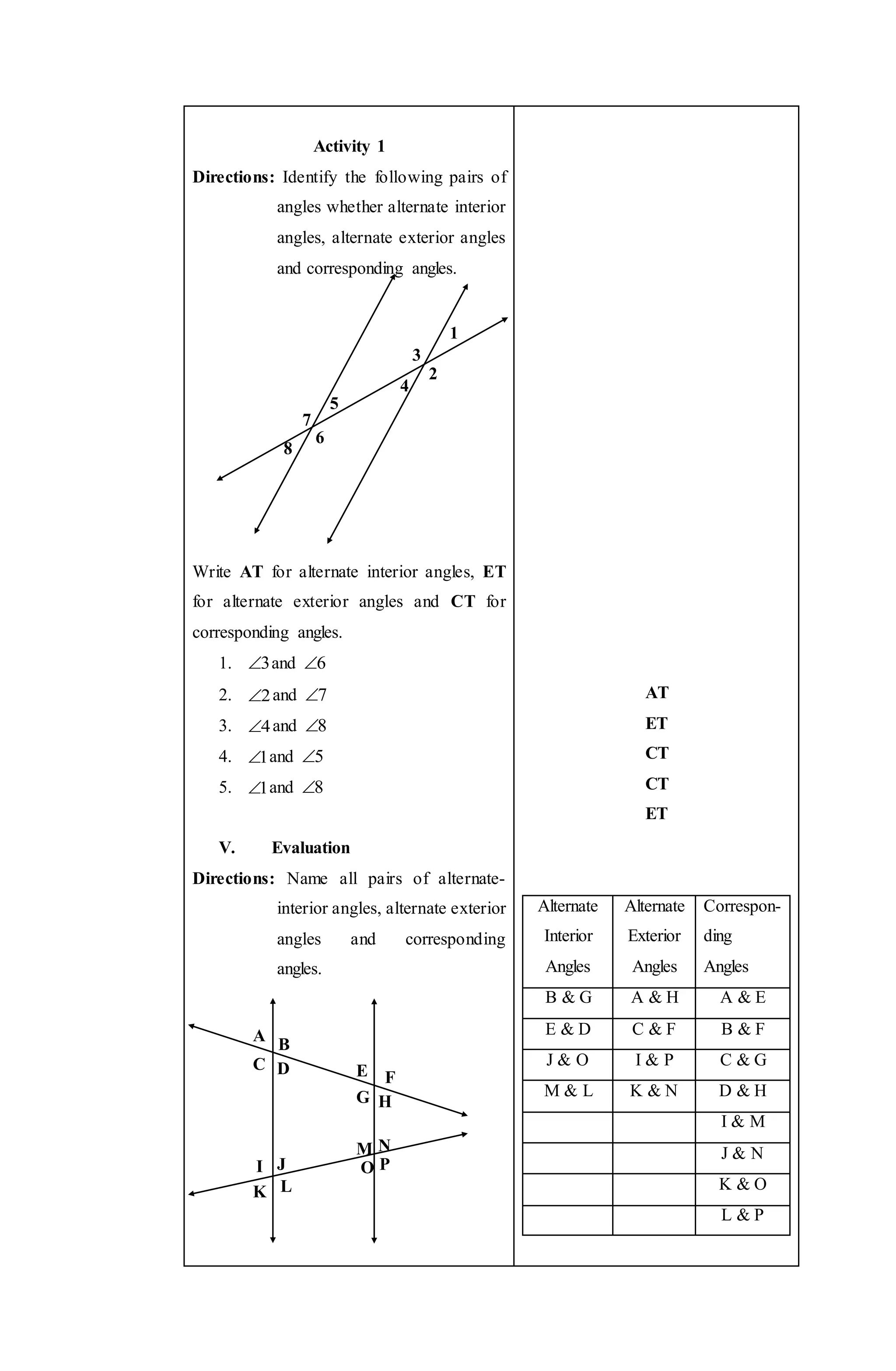
The document outlines a lesson plan on teaching students about pairs of angles formed when parallel lines are cut by a transversal. It includes the objectives, subject matter, materials, and a step-by-step procedure using the 5A's method of teaching. The procedure involves students drawing parallel lines cut by a transversal, identifying and defining different pairs of angles, including alternate interior angles, alternate exterior angles, and corresponding angles. Students are then given activities to practice identifying these pairs of angles and an assignment to measure angles in a drawing.

1. I. Objectives: At the end of the lesson, students are expected to:
a. identify the following pairs of angles;
b. name pairs of angles from the figure;
c. describe the importance of parallelism.
II. Subject Matter: Pairs of Angles formed by Parallel Lines Cut by a
Transversal
Reference: Mathematics for Grade 7 page (350-353)
Skills: drawing, analyzing and solving
Values: parallelism
III. Materials: ruler, protractor, pintail pen, manila paper
IV. Procedure: 5A’s Method
Teacher’s Activity Students’ Activity
A. Awareness
a. Drill
(prayer)
(greetings)
(announcing of classroom rules)
(checking of attendance)
(collecting of assignment)
Before we’ll proceed to our new lesson for
today, let’s have first an activity regarding
our lesson last meeting.
(Group the students into 5 groups)
I have here a word box with three jumbled
words in it. All you have to do is to arrange
them first so you could answer the
following questions below the word box.
Is it clear class?
I’ll give 5 minutes to do it and your time
will start now.
Yes, sir!
Students do as told

2. _________1. These lines do not intersect
each other and they lie on the same plane.
_________2. These lines lie on the different
planes.
_________3. A line that intersects two or
more coplanar lines at two or more distinct
points.
b. Motivation
The terms are skew lines, parallel lines and
transversal line.
Do you know class tat parallel lines and
transversal line have something to do with
our new lesson for today?
Do you know class that there are pairs of
angles formed when transversal line
intersects parallel lines?
c. Presentation
So, this morning, we will discuss the pairs
of angles formed by parallel lines cut by a
transversal line.
Everybody read!
d. Statement of the Aim
*identify the following pairs of angles;
*name pairs of angles given the figure;
*describe the importance of parallelism.
Parallel lines
Skew lines
Transversal line
No, sir!
No, Sir!
“Pairs of Angles formed by Parallel
Lines Cut by a Transversal”
Lraplale sinel
Weks nisel
Vansreltras lein

3. B. Activity
The group you had in our first activity will
be the same group you’ll have in this
activity. I am going to provide you the
necessary materials: ruler, manila paper and
pintail pen.
All you have to do is to follow these
following procedures for you to do the
activity,
Am I understood class?
When you are done, say with action, “Clap,
clap, clap Champion”! The group which can
finish first will be declared as the winner
and will receive a secret prize afterwards.
I’ll give you five minutes to do it and your
time starts now.
(let one student draw the figure on the
board)
(let another student discuss the figure being
drawn on the board)
Yes, Sir!
Students do as told
Student does told
Student does told
Do the following in your group;
1. Draw a horizontal line and
label it as line l.
2. Draw another horizontal
line below the line l and
name it as line k.
3. Draw a diagonal line,
intersecting the two lines:
line l and line k and name it
as line t.
4. Name the points of
intersecting as Point X and
Y respectively.

4. For uniformity, let’s label together the
angles being formed by parallel lines cut a
transversal.
(Labelling)
C. Analysis
So now, let’s discuss about the pairs of
angles.
Let’s begin with angle 3 and angle 6.
Are the two angles?
Are the two angles interior or not?
Are the two angles placed on the opposite
sides of the transversal?
Very good!
So angle 3 and angle 6 are non-adjacent
interior angles on the opposite sides of the
transversal.
What other pair of angles which has the
same characteristics with the angle 3 angle
6?
Angle 3 and angle 6 are not
congruent because they do not have
common side.
Angle 3 and angle 6 are interior
angles because they lie inside the
figure.
Angle 3 and angle 6 are placed on the
opposite sides of the transversal.
Angle 3 is at the right while angle 6 is
at the left side.
Another pair of angles which has the
same characteristics with angle 3 and
6 is angle 4 and angle 5.
1
X 2
3 4
5 6
89
Y
l
k
t

5. How are you going to describe the
characteristics of angle 3 and angle 4?
Another!
Now let’s proceed to the angles located
outside the figure.
What are those angles?
What have you observed about 1 and angle
8?
Another!
Another!
Very good!
How are you going to give another pair of
angles which has the same characteristics
with angle1 and angle 8?
Why do you say so?
Bravo!
Let’s move-on to another pair of angles.
What have observed about angle 3 and
angle 7?
Angle 4 and angle 5 are not adjacent
because they do not have common
side.
Angle 4 and angle 5 are interior
angles because they located inside the
figure.
The angles located outside the figure
are angle 1, 2, 7, and angle 8.
Angle 1 and angle 8 are not adjacent
because they do not have common
side.
Angle 1 and angle 8 are exterior
angles because they are located
outside the figure
Angle 1 and angle8 are located on the
opposite sides of the transversal.
Another pair of angles which has the
same characteristics with angle 1
angle 8 is angle 2 angle 7.
It’s because angle 2 and angle 7 are
non-adjacent exterior angles on the
opposite sides of the transversal.
Angle 3 and angle 7 are not adjacent
because they do not have common
side.

6. Are the two angles; one is interior and the
other one is exterior?
How are you going to describe the
placement of the two angles?
What other pair of angles which has the
same characteristics with angle 3 and angle
7?
Why do you say so?
Very good!
Another pairs of angles which have the
same characteristics with angle 3 and angle
7 aside from angle 4 and angle 8 are angle 1
and angle 5 and angle 2 and angle 6.
Let’s recall the pairs of angles that we have
discussed a while ago.
(Recalling)
D. Abstraction
Based from the characteristics of the pair of
angles like angle 3 and angle 6 and angle 4
and angle 5, how are you going to formulate
the definition of alternate interior angles?
Angle 3 and angle 7 are interior angle
and exterior angle because they are
located
Angle 3 and angle 7 are located on
the same sides of the transversal.
Another pair of angle which has the
same characteristics with angle 3 and
angle 7 is angle 4 and angle 8.
It is because angle 4 and angle 8 are
non-adjacent angles where one is
interior and the other one is exterior
on the same side of the transversal.
Based from the characteristics of
those pairs of angles, alternate
interior angles are two non-adjacent
angles interior angles on the opposite
sides of the transversal.

7. How are you going to define alternate
exterior angles based from the
characteristics of pairs of angles: angle 1
and angle 8, angle 2 and angle 8?
How are you going to define the
corresponding angles based from the
characteristics of pair of angles; angle 3 and
angle 7?
Very absolutely excellent!
Everybody read the definition of the
following pairs of angles formed by parallel
lines cut by a transversal;
Alternate exterior angles are two
nonadjacent exterior angles on the
opposite sides of the transversal.
Corresponding angles are two
nonadjacent angles, one is interior
and the other one is exterior on the
same side of the transversal.
Pairs of angles formed by parallel
lines cut by a transversal
(based from the figure on the
previous activity)
Alternate interior angles are two
nonadjacent interior angles on the
opposite sides of the transversal.
Ex: 3 and 6
4 and 5
Alternate exterior angles are two
nonadjacent exterior angles on the
opposite sides of the transversal.
Ex: 1 and 8
2 and 7
Corresponding Angles are two
nonadjacent angles which one is
interior and the other one is exterior
on the same side of the transversal.

8. Values Integration
In our discussion, we have discussed about
pairs of angles formed by parallel lines cut
by a transversal.
You have noticed that parallel lines are two
essential in our discussion.
In connection to our real life class, can you
give a situation which involves parallelism?
Based from the given situation in general
idea, how importance is parallelism?
Exactly correct!
E. Application
In our real world class, how are parallel
lines being applied?
Very good!
Example, like dress code. For an
idealist perspective, whatever you
wear in your top, it should match with
your bottom, and otherwise you’ll
look weird.
Parallelism is vital to every life of a
person. In everything that a person
does, parallelism must be maintained.
The consistency of your words,
actions and even your philosophy in
life is essential to keep your good
credibility.
The concept of parallel lines is used
in making bridges, roads, buildings,
houses, windows, doors, household
furniture and etc.

9. Activity 1
Directions: Identify the following pairs of
angles whether alternate interior
angles, alternate exterior angles
and corresponding angles.
Write AT for alternate interior angles, ET
for alternate exterior angles and CT for
corresponding angles.
1. 3 and 6
2. 2 and 7
3. 4 and 8
4. 1 and 5
5. 1 and 8
V. Evaluation
Directions: Name all pairs of alternate-
interior angles, alternate exterior
angles and corresponding
angles.
AT
ET
CT
CT
ET
Alternate
Interior
Angles
Alternate
Exterior
Angles
Correspon-
ding
Angles
B & G A & H A & E
E & D C & F B & F
J & O I & P C & G
M & L K & N D & H
I & M
J & N
K & O
L & P
3
4
1
2
7
8
5
6
A
B
C D
I J
K L
E F
G H
M N
PO

10. VI. Assignment
Directions: Draw a parallel lines cut by a
transversal and use a protractor
to measure the following:
 Alternate interior angles
 Alternate exterior angles
 Corresponding angles