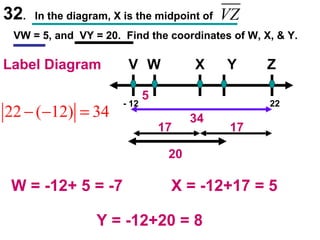
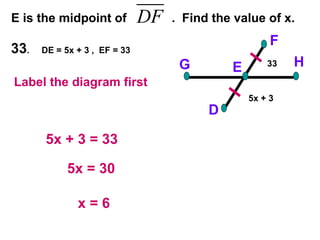
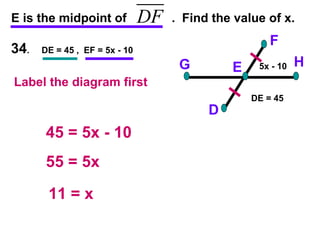
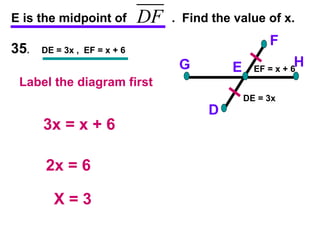
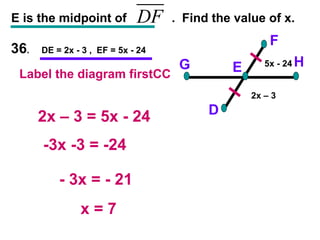
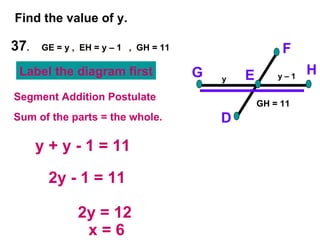
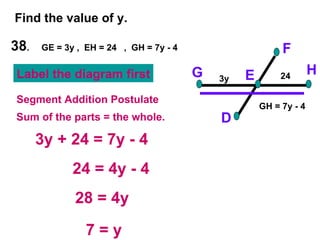
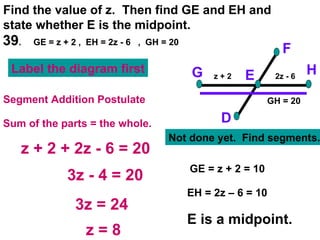
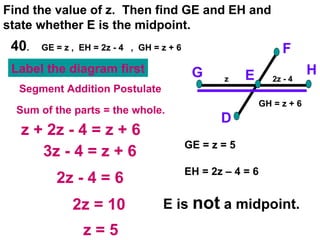
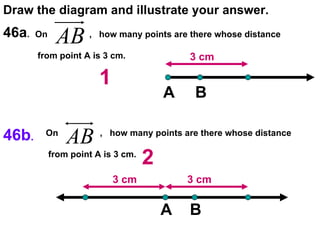
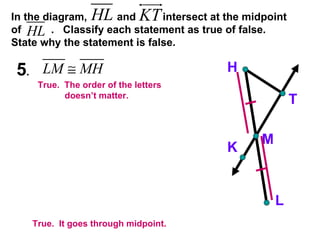
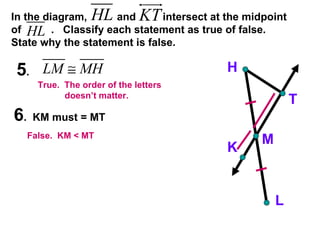
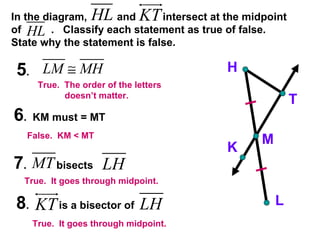
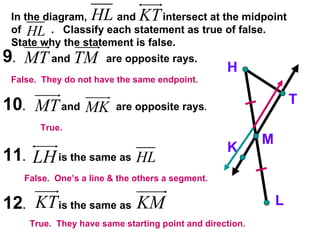
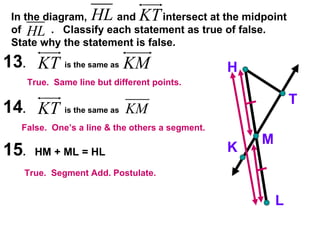
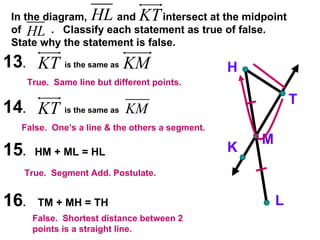
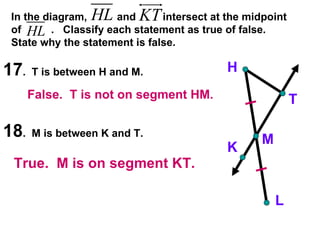
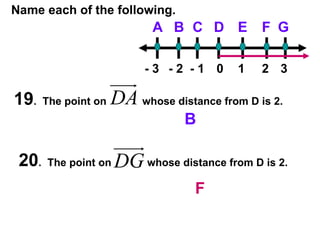
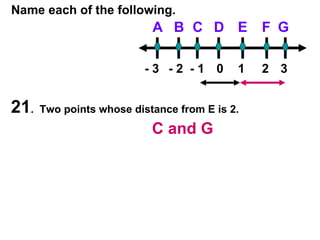
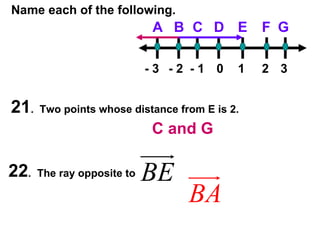
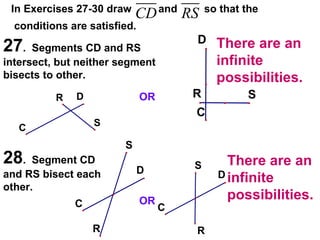
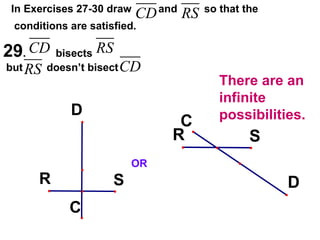
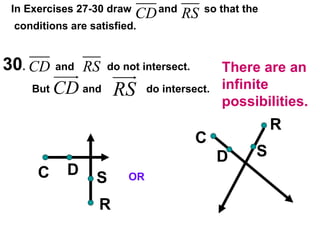
The document contains examples and exercises on classifying statements as true or false based on diagrams of line segments, rays, and their intersections. It also contains examples of finding distances between points on a number line, coordinates of midpoints, values of variables that satisfy given conditions about line segments.

1. Millau Bridge Sir Norman Foster Point, Lines, Planes, Angles Fallingwaters Frank Lloyd Wright Millenium Park Frank Lloyd Wright 1.3 Segments, Rays, and Distance WE Page 15

2. 1.3 Segments, Rays, and Distance WE Page 15 The numbers given are coordinates of 2 points on a number line. Find the distance between the points. 1 . - 6 and 9 2 . - 3 and - 17 3 . - 1.2 and - 5.7 4 . - 2.5 and 4.6

3. In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. 5 . H K M T L True. It goes through midpoint. True. The order of the letters doesn’t matter.

4. In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. 5 . 6 . KM must = MT H K M T L False. KM < MT True. The order of the letters doesn’t matter.

5. In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. 5 . 6 . KM must = MT 7 . bisects 8 . is a bisector of H K M T L True. It goes through midpoint. True. It goes through midpoint. False. KM < MT True. The order of the letters doesn’t matter.

6. 9 . and are opposite rays. 10 . and are opposite rays . 11 . is the same as 12 . is the same as H K M T L False. They do not have the same endpoint. True. False. One’s a line & the others a segment. True. They have same starting point and direction. In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false.

7. 13 . is the same as 14 . is the same as 15 . HM + ML = HL H K M T L In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. True. Same line but different points. False. One’s a line & the others a segment. True. Segment Add. Postulate.

8. 13 . is the same as 14 . is the same as 15 . HM + ML = HL 16 . TM + MH = TH H K M T L In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. True. Same line but different points. False. One’s a line & the others a segment. True. Segment Add. Postulate. False. Shortest distance between 2 points is a straight line.

9. 17 . T is between H and M. 18 . M is between K and T. H K M T L In the diagram, and intersect at the midpoint of . Classify each statement as true of false. State why the statement is false. False. T is not on segment HM. True. M is on segment KT.

10. Name each of the following. 19 . The point on whose distance from D is 2. D B C G F E A - 3 - 2 - 1 0 1 2 3 B

11. Name each of the following. 19 . The point on whose distance from D is 2. 20 . The point on whose distance from D is 2. D B C G F E A - 3 - 2 - 1 0 1 2 3 B F

12. Name each of the following. 21 . Two points whose distance from E is 2. D B C G F E A - 3 - 2 - 1 0 1 2 3 C and G

13. Name each of the following. 21 . Two points whose distance from E is 2. 22 . The ray opposite to D B C G F E A - 3 - 2 - 1 0 1 2 3 C and G

14. Name each of the following. 23 . The midpoint of D B C G F E A - 3 - 2 - 1 0 1 2 3 D seen visually. or Average the coordinates. Note that the name of the midpoint is a letter while the coordinate is a number. D

15. Name each of the following. 24 . The coordinate of the midpoint of D B C G F E A - 3 - 2 - 1 0 1 2 3 -1 seen visually. or Average the coordinates.

16. Name each of the following. 25 . The coordinate of the midpoint of D B C G F E A - 3 - 2 - 1 0 1 2 3 -1

17. Name each of the following. 25 . The coordinate of the midpoint of 26 . A segment congruent to D B C G F E A - 3 - 2 - 1 0 1 2 3 -1

18. In Exercises 27-30 draw and so that the conditions are satisfied. 27 . Segments CD and RS intersect, but neither segment bisects to other. 28 . Segment CD and RS bisect each other. OR OR There are an infinite possibilities. There are an infinite possibilities.

19. 29 . bisects but doesn’t bisect OR In Exercises 27-30 draw and so that the conditions are satisfied. There are an infinite possibilities.

20. 30 . and do not intersect. OR C R D S R D C S In Exercises 27-30 draw and so that the conditions are satisfied. But and do intersect. There are an infinite possibilities.

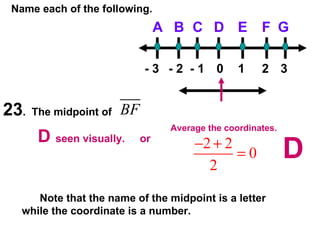
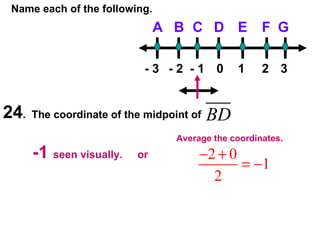
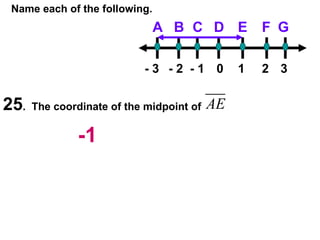
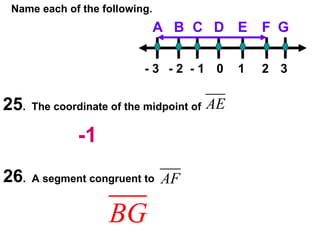
21. 31 . In the diagram, , S is midpoint of . QR = 4 and ST = 5. Complete. P Q R S T Label Diagram First !! 4 5 5 10 10 6 a] RS = _____ b] RT = _____ c] PR = _____ d] PQ = _____ 5 10 10 6 Note that once the diagram was labeled , everything was easier.

22. 32 . In the diagram, X is the midpoint of VW = 5, and VY = 20. Find the coordinates of W, X, & Y. V W X Y Z 5 20 34 - 12 22 17 17 Label Diagram X = -12+17 = 5 W = -12+ 5 = -7 Y = -12+20 = 8

23. 33 . DE = 5x + 3 , EF = 33 E is the midpoint of . Find the value of x. F D H G E 5x + 3 = 33 5x = 30 x = 6 33 5x + 3 Label the diagram first

24. 34 . DE = 45 , EF = 5x - 10 E is the midpoint of . Find the value of x. F D H G E 45 = 5x - 10 55 = 5x 11 = x 5x - 10 DE = 45 Label the diagram first

25. 35 . DE = 3x , EF = x + 6 E is the midpoint of . Find the value of x. F D H G E 3x = x + 6 2x = 6 X = 3 EF = x + 6 DE = 3x Label the diagram first

26. 36 . DE = 2x - 3 , EF = 5x - 24 E is the midpoint of . Find the value of x. F D H G E 2x – 3 = 5x - 24 -3x -3 = -24 - 3x = - 21 x = 7 Label the diagram firstCC 5x - 24 2x – 3

27. 37 . GE = y , EH = y – 1 , GH = 11 Find the value of y. F D H G E y + y - 1 = 11 2y - 1 = 11 2y = 12 x = 6 Segment Addition Postulate Sum of the parts = the whole. y y – 1 Label the diagram first GH = 11

28. 38 . GE = 3y , EH = 24 , GH = 7y - 4 Find the value of y. F D H G E 3y + 24 = 7y - 4 24 = 4y - 4 28 = 4y 7 = y Segment Addition Postulate Sum of the parts = the whole. 3y 24 Label the diagram first GH = 7y - 4

29. 39 . GE = z + 2 , EH = 2z - 6 , GH = 20 Find the value of z. Then find GE and EH and state whether E is the midpoint. F D H G E z + 2 + 2z - 6 = 20 3z - 4 = 20 3z = 24 z = 8 Segment Addition Postulate Sum of the parts = the whole. GE = z + 2 = 10 EH = 2z – 6 = 10 E is a midpoint. z + 2 2z - 6 Label the diagram first GH = 20 Not done yet. Find segments.

30. 40 . GE = z , EH = 2z - 4 , GH = z + 6 Find the value of z. Then find GE and EH and state whether E is the midpoint. F D H G E z + 2z - 4 = z + 6 3z - 4 = z + 6 2z - 4 = 6 2z = 10 Segment Addition Postulate Sum of the parts = the whole. GE = z = 5 EH = 2z – 4 = 6 E is not a midpoint. z = 5 z 2z - 4 Label the diagram first GH = z + 6

31. 41 . Name the graph of the given equation or inequality. N H M Z Y T G - 4 - 2 0 2 4 6 8 42 . 43 .

32. 44 . Name the graph of the given equation or inequality. N H M Z Y T G - 4 - 2 0 2 4 6 8 45 . The whole line. Point M The absolute value of negative numbers are greater than 0; the absolute value of 0 = 0 ; and the absolute value of positive numbers are greater than zero.

33. 46a . Draw the diagram and illustrate your answer. 46b . On , how many points are there whose distance from point A is 3 cm. 3 cm A B 1 On , how many points are there whose distance from point A is 3 cm. 3 cm 3 cm A 2 B

34. C’est fini. Good day and good luck.