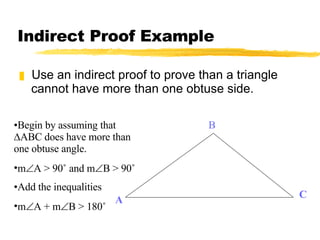
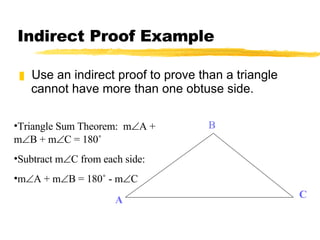
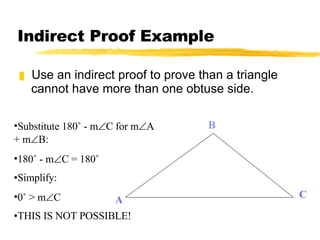
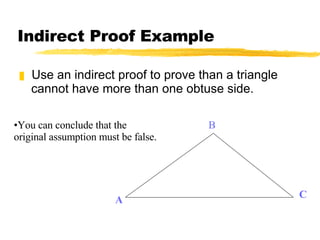
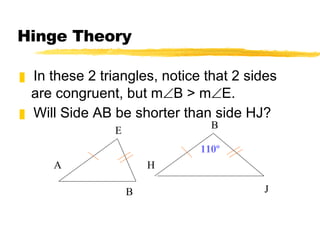
This document discusses indirect proofs and using theorems about triangles to compare side lengths and angle measures. It provides an example of an indirect proof showing that a triangle cannot have more than one obtuse angle. It also discusses the Hinge Theorem and its converse, which relate the measures of included angles and lengths of corresponding sides in triangles with two congruent sides. Exercises are provided for the reader to practice these concepts.

1. Indirect Proof and Inequalities in Two Triangles Objectives: - Read and write an indirect proof - Use the Hinge Theorem and its converse to compare side lengths and angle measures

2. Indirect Proof An indirect proof is a proof in which you prove that a statement is true by first assuming that its opposite is true. If this assumption leads to an impossibility, then you have proved that the original statement is true.

3. Indirect Proof Example Use an indirect proof to prove than a triangle cannot have more than one obtuse side. A B C Begin by assuming that ∆ABC does have more than one obtuse angle. m  A > 90˚ and m  B > 90˚ Add the inequalities m  A + m  B > 180˚

4. Indirect Proof Example Use an indirect proof to prove than a triangle cannot have more than one obtuse side. A B C Triangle Sum Theorem: m  A + m  B + m  C = 180˚ Subtract m  C from each side: m  A + m  B = 180˚ - m  C

5. Indirect Proof Example Use an indirect proof to prove than a triangle cannot have more than one obtuse side. A B C Substitute 180˚ - m  C for m  A + m  B: 180˚ - m  C = 180˚ Simplify: 0˚ > m  C THIS IS NOT POSSIBLE!

6. Indirect Proof Example Use an indirect proof to prove than a triangle cannot have more than one obtuse side. A B C You can conclude that the original assumption must be false.

7. Hinge Theory In these 2 triangles, notice that 2 sides are congruent, but m  B > m  E. Will Side AB be shorter than side HJ? 110º H B A E B J

8. Hinge Theorem If 2 sides of one triangle are congruent to 2 sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the 3rd side of the first is longer than the 3rd side of the second.

9. Converse of the Hinge Theorem If 2 sides of one triangle are congruent to 2 sides of another triangle, and the 3rd side of the first is longer than the 3rd side of the second, then the included angle of the first is larger than the included angle of the second.

10. Do p. 305 1-6 Homework: Worksheets