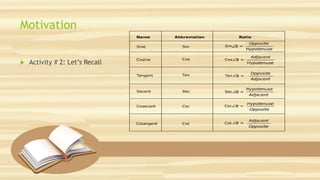
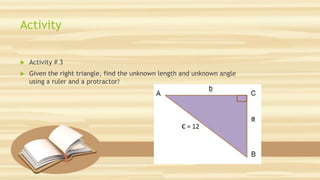
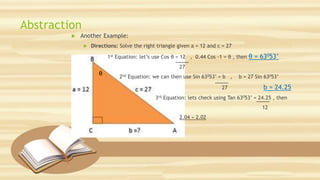
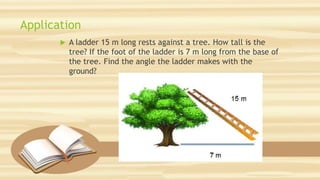
This document discusses six trigonometric functions - sine, cosine, tangent, secant, cosecant and cotangent. It includes three activities to demonstrate these functions using right triangles: finding the functions for a given triangle, finding unknown lengths and angles with and without tools, and solving application problems involving right triangles. The objectives are to demonstrate the six trigonometric ratios and solve real-life problems using them.

1. Six Trigonometric Functions
Grade 9 4th Quarter
Mike Milan

2. Objectives:
 To demonstrate the six trigonometric ratios: sine,
cosine, tangent, secant, cosecant, and cotangent;
and
 To solve the six trigonometric ratio in real life
situations.

3. Motivation
 Activity #1
 How many right triangles do you see?

4. Motivation
 Activity # 2: Let’s recall!
Directions: Find the 6
trigonometric functions of the
triangle.

5. Motivation
 Activity # 2: Let’s Recall

6. Motivation
 Activity #2: Let’s Recall
Sin θ = 12
13
Cos θ = 5
13
Tan θ = 12
5
Sec θ = 13
12
Csc θ = 13
5
Cot θ = 5
12

7. Activity
 Activity # 3
 Given the right triangle, find the unknown length and unknown angle
using a ruler and a protractor?

8. Analysis
 Was it easy for you to find the unknown length
and unknown angle of the right triangle given to
you?
 Without using a ruler and a protractor, do you
think you can able to find the unknown side and
angle?

9. Let’s watch this video first!

10. Abstraction
 Going through the problem, it says that the we need to find the “unknown
length” and “unknown angle”, so we surmised that this right triangle is an
isosceles right triangle.
 1st equation: Let’s presume as isosceles right triangle that the angle θ is 450.
Using Sin θ = b then, b = 12 (Sin 450), so b = 8.49
12
2nd equation: Let’s proceed in checking the
correctness of the value of θ by using Tan function.
Tan θ = 8.49 , then tan-1 1= θ, results to θ = 450, thus it is right to say that
8.49 we were right to acknowledge that it is an isosceles triangle.
θ

11. Abstraction
 Another Example:
 Directions: Solve the right triangle given a = 12 and c = 27
1st Equation: let’s use Cos θ = 12 , 0.44 Cos -1 = θ , then θ = 63053’
27
2nd Equation: we can then use Sin 63053’ = b , b = 27 Sin 63053’
27 b = 24.25
3rd Equation: lets check using Tan 63053’ = 24.25 , then
12
2.04 ≈ 2.02
θ

12. Application
 A ladder 15 m long rests against a tree. How tall is the
tree? If the foot of the ladder is 7 m long from the base of
the tree. Find the angle the ladder makes with the
ground?

13. Quiz
 Solve for the constant and the value of the unknown
variable.
 Use the given figure to solve the remaining parts of right
triangle ACB.
 1. b = 17 cm and c = 23 cm
2. c = 16 and a = 7