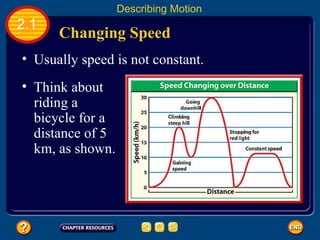
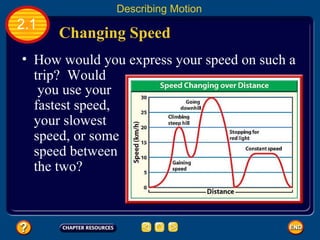
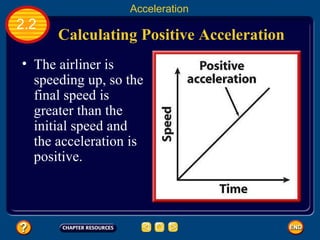
Distance and time are important factors in describing motion, especially in running events. To win a race, runners must cover the distance in the shortest time. Speed is the distance traveled per unit of time and is important for describing motion, along with other factors like average and instantaneous speed. Acceleration is the rate of change of velocity and can be positive if an object is speeding up or negative if slowing down.