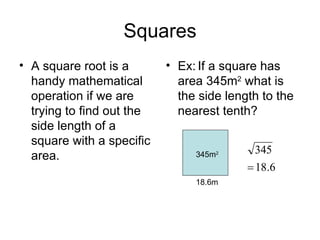
This document discusses various methods for estimating and calculating square roots. It begins by defining irrational numbers as non-repeating decimals that can result from taking the square root of a non-perfect square. It then discusses estimating square roots by knowing perfect square numbers and using guess and check methods. Later sections cover using calculators, applying square roots in formulas, exponent rules including multiplication, division, powers, and scientific notation for writing extremely large numbers.

1. Estimating and Calculating Square Roots 1.1

2. Irrational Numbers It is a non-repeating, non-ending decimal. An irrational number can result from a square root of a non-perfect square. Other example of irrational numbers are things like

3. Estimating Square Roots It is very handy to know by heart some of the first few perfect square numbers. This will help you see patterns and have some idea if your calculated answers are close.

4. Estimating Square Roots cont’d Now, we should be able to answer what the square root is of any small perfect square.

5. Estimating Square Roots cont’d We can also use these when we are looking for square roots of numbers that are close to a perfect square.

6. Estimating Square Roots cont’d Relatively small numbers that are further from perfect squares can be estimated by using a form of guess and check.

7. Estimating Square Roots cont’d Estimating roots of extremely large and extremely small numbers can be done by the following process. Starting from the decimal, split the number into pairs of digits. Estimate the square root of the group furthest from the decimal. Write one zero for all of the other groups.

8. Calculators Generally calculators will give you a quick estimate of square roots to 10 digits by pressing the root button. You need to check how to use your calculator and make sure that you are using the buttons correctly.

9. Multiples of Roots Whenever a number appears in front of a root without an operation between, you multiply the number and the root together.

10. Evaluating Square Roots When you are asked to evaluate square roots you are being asked to “find the value.” Be sure you can evaluate all of the following expressions correctly and get the same answers shown.

11. Applying Square Roots 1.2

12. Squares A square root is a handy mathematical operation if we are trying to find out the side length of a square with a specific area. Ex: If a square has area 345m 2 what is the side length to the nearest tenth? 345m 2 18.6m

13. Square Roots in Formulas Many formulas also use square roots. Ex: Heron’s formula for the area of a triangle is given below where a,b,c are the sides of the triangle and s is half the perimeter. Calculate the area of the following triangle to the nearest tenth using Heron’s formula. 8cm 7cm 5cm

14. Exponents and Powers 1.4

15. Definitions Mathematicians developed over time a notation to represent many repeated multiplications. This was called exponents. The base was the number that was being multiplied over and over again. The exponent was the number of time that the base was multiplied. base exponent

16. Evaluating Exponents The exponential form of a number is the base and exponent form we just saw. When we write out all of the multiplications of the base we call it the repeated multiplication form. If we evaluate the number and write it normally, we call it the standard form. Exponential form Repeated multiplication form Standard form

17. Exponents of Variables We treat exponents on variables exactly the same as any number. The only difference is that we cannot evaluate the expression until we get a value for the variable.

18. What’s the Base? Determining the base can be tricky. The exponent applies only to the very next number to the left. -4 2 2 6 a 4 xy 2 x 3 Base Exponent Expression

19. Coefficient Mathematicians will call any number in front of a set of variables a coefficient. coefficient -4 3 Coefficient Expression

20. Exponent Rules 1.5

21. Multiplication Law If two exponential numbers with the same base are multiplied then the expression is simplified by adding the exponents.

22. Multiplication Law cont’d Try these examples. You need to write the expression as a single exponential expression. The answers are at the bottom.

23. Division Law If two exponential numbers with the same base are divided then the expression is simplified by subtracting the exponents.

24. Division Law Try these examples. You need to write the expression as a single exponential expression. The answers are at the bottom.

25. Power to a Power Rule If an exponential numbers is raised to a second exponent, the expression is simplified by multiplying the exponents.

26. Power to a Power Rule cont’d Try these examples. You need to write the expression as a single exponential expression. The answers are at the bottom.

27. Scientific Notation Large Numbers 1.7

28. Extremely Large Numbers In science it is common to look at extremely large numbers. Consider the following number. 6 022 141 500 000 000 000 000 000 This number is the number of particles found in 12 grams of carbon-12. It is known as Avagadro’s number named in honor of the chemist Amedeo Avagadro. Although the number seems ridiculous it is extremely important to chemists as it represents the number of particles found in 1 gram mole of any substance.

29. Extremely Large Numbers cont’d Numbers like these in science are commonplace. It is therefore very useful to us to find a shortcut way of writing very large numbers. We call this shortcut scientific notation. It uses the ability to drop trailing zeros after a decimal to shorten the number we have to write.

30. Scientific Notation What we do is find the first significant digit looking from left to right. Write a decimal after this first significant digit. Multiply by an appropriate power of 10 that represents all of the places the decimal moved. Drop all trailing 0’s (rounding to an appropriate decimal place).

31. Scientific Notation cont’d Write each of the following in scientific notation. The answers are at the bottom.

32. Operations With Scientific Notation Multiplying very large numbers is much easier with scientific notation. We make use of the fact that we can multiply a series of numbers in any order we want. We also use the exponent laws we just learned about.

33. Operations With Scientific Notation cont’d We need to be careful that our answers are always written in correct scientific notation. If they are not correct after the multiplication or division then we need to adjust the number in front and the coefficient so that it is the correct form but that the value doesn’t change. *Remember* If the front number has to be changed smaller then the power of 10 needs to be bigger. If the front number needs to be made bigger then the power of ten need to be smaller.

34. Operations With Scientific Notation cont’d Complete each of the following writing the answer in scientific notation. The answers are at the bottom.

35. Working With Exponents 1.8

36. What’s the Difference? One of the most difficult things for grade 9 students is trying to understand the difference between the following two expressions.

37. What’s the Difference? cont’d They appear to have the same value but a closer inspection will reveal that they are in fact very different. -81 81 Value Repeated Mult Expression

38. Powers of Monomials 1.9

39. Monomials Recall that a monomial is an expression that involves multiplication and division only. These are monomials These are NOT monomials

40. Power Rule Recall also the law of exponents that says that a power raised to a power is equivalent to a base raised to the multiple of the power.

41. Powers of Monomials Consider the following monomial. In repeated multiplication for and then simplified into exponential form we get the following results.

42. Powers of Monomials cont’d It appears as though we can apply the power to a power exponent law to each factor of a monomial.

43. Powers of Monomials cont’d Try these examples. Calculate and simplify the following powers of monomials. The answers are given at the bottom.

44. Powers of Rational Monomials The same rules hold true for a fraction. So we can try the following examples. Calculate and simplify the following powers of monomials. The answers are given at the bottom.

45. Products of Monomial Powers We can put all of the exponent rules together along with the powers of monomials and simplify very complex expressions. We only need to remember that we can multiply numbers in any order and to use the exponent laws as they come up.

46. Products of Monomial Powers For example, we can do the following calculation and simplification. All of the steps shown are usually done mentally. However, to avoid errors, it is always good to write a few intermediate steps down.

47. Products of Monomial Powers Try these examples. The answers are given at the bottom of the page.

48. Volumes Volumes of cubes are applications of monomial expressions. For volumes we need to remember the formula for the volume of a cube. s

49. Volumes Try this example. The answer is given at the bottom. What is the volume of the cube given? Hint:

50. Zero and Negative Exponents 1.11

51. Zero Exponents Consider the two following calculations of the same exponential expression. In the first case, the numbers were evaluated and reduced, in the second, exponent laws were used.

52. Zero Exponents Let’s take the second equation and write it backward and put the first equation underneath so that the middle lines up. What we can see is that

53. Zero Power The upshot of that exercise is that anything raised to the zero power is 1.

54. Negative Powers Consider the following examples of calculating the same expression. In the first case we evaluate the expressions, reduce the fraction, and rewrite the number in exponential form

55. Negative Powers Let’s take the second equation and write it backward and put the first equation underneath so that the middle lines up. What we can see is that

56. Negative Exponents The upshot of this is that any exponent that is negative has a positive exponent in the reciprocal. (Negative exponents on the top of a fraction are positive on the bottom. Negative exponents in the bottom of a fraction are positive in the top.)

57. Negative Exponents We can even apply this rule to separate factors of an expression. We still need to use the other exponent laws to combine the factors with the same bases.

58. Negative Exponents Try these examples. Simplify the expressions as much as possible and write all factors with positive exponents.

59. Scientific Notation Small Numbers 1.12

60. Very Small Numbers Water H 2 O will split into H + and OH - one time in 10 million molecules (at random). Represented as a ratio of split molecules to whole molecules is or 0.0000001. This number is very small and can be written using negative exponents and scientific notation. The pH of neutral water is 7.

61. Small Numbers If you add a little bit of sodium Hydroxide to water then the amount of H + ions decreases to a ratio of or 0.00000000000001 This number is very small and can be written in scientific notation as The pH of sodium hydroxide solution is 14.

62. Operations With Scientific Notation The operations with scientific notation numbers doesn’t change if the numbers are very large or very small. Multiply the numeric parts first then multiply the powers of 10. Be sure to add and subtract the integer exponents correctly.

63. Operations With Scientific Notation Try these examples. The answers are at the bottom.