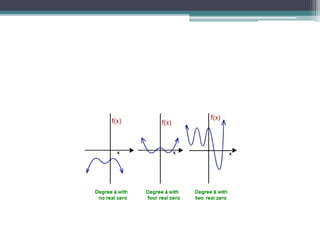
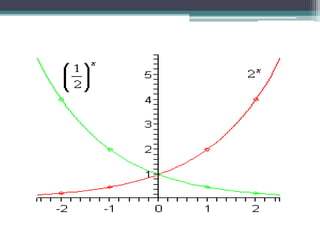
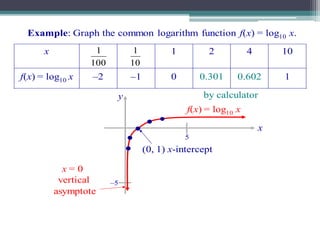
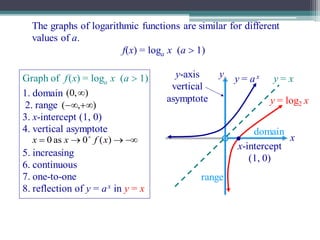
This document provides information about several advanced algebra topics:
1. The Remainder Theorem states that when dividing a polynomial f(x) by x-c, the remainder is equal to f(c).
2. The Factor Theorem states that if f(c) = 0, then x-c is a factor of the polynomial.
3. Synthetic division is a method for dividing polynomials without subtracting, by multiplying the coefficients.
4. The Rational Zeros Theorem can be used to find all possible rational zeros of a polynomial by considering factors of the leading coefficient and constant term.