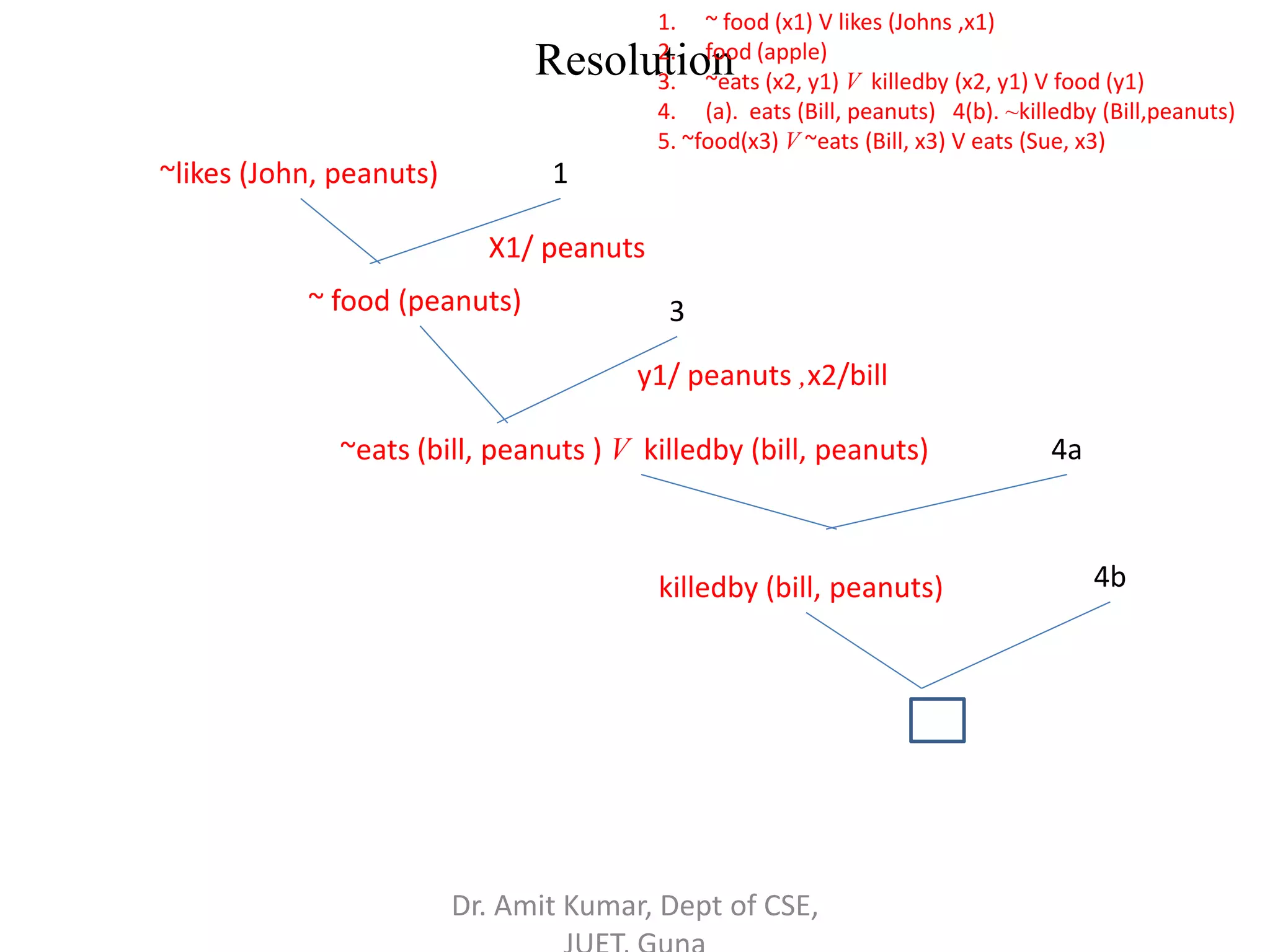
This document provides an overview of propositional logic concepts including:
- Logic is used to distinguish correct from incorrect reasoning and explicate laws of thought.
- A proposition is a declarative statement that is either true or false. Propositional logic uses logical operators to combine propositions into compound statements.
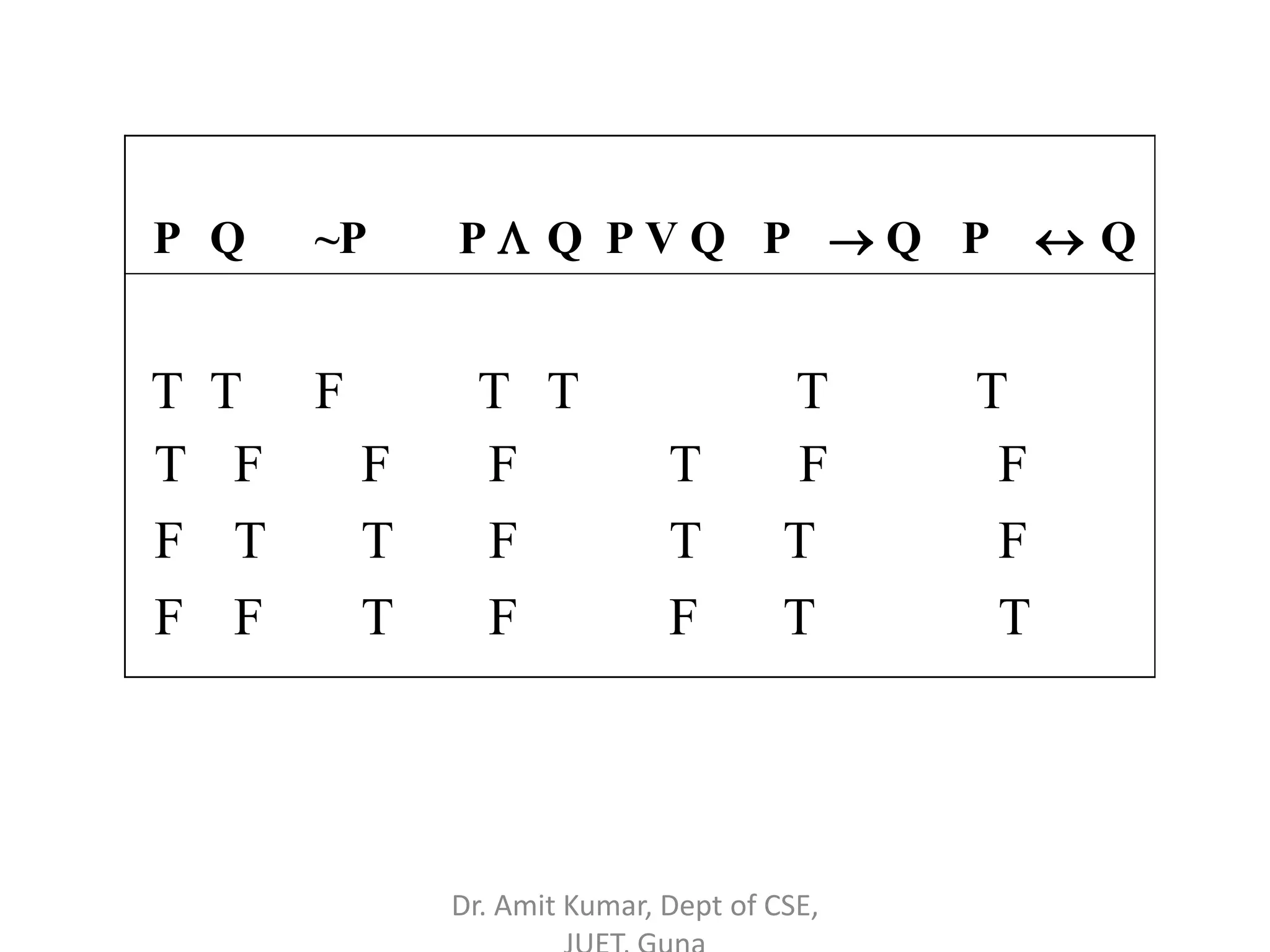
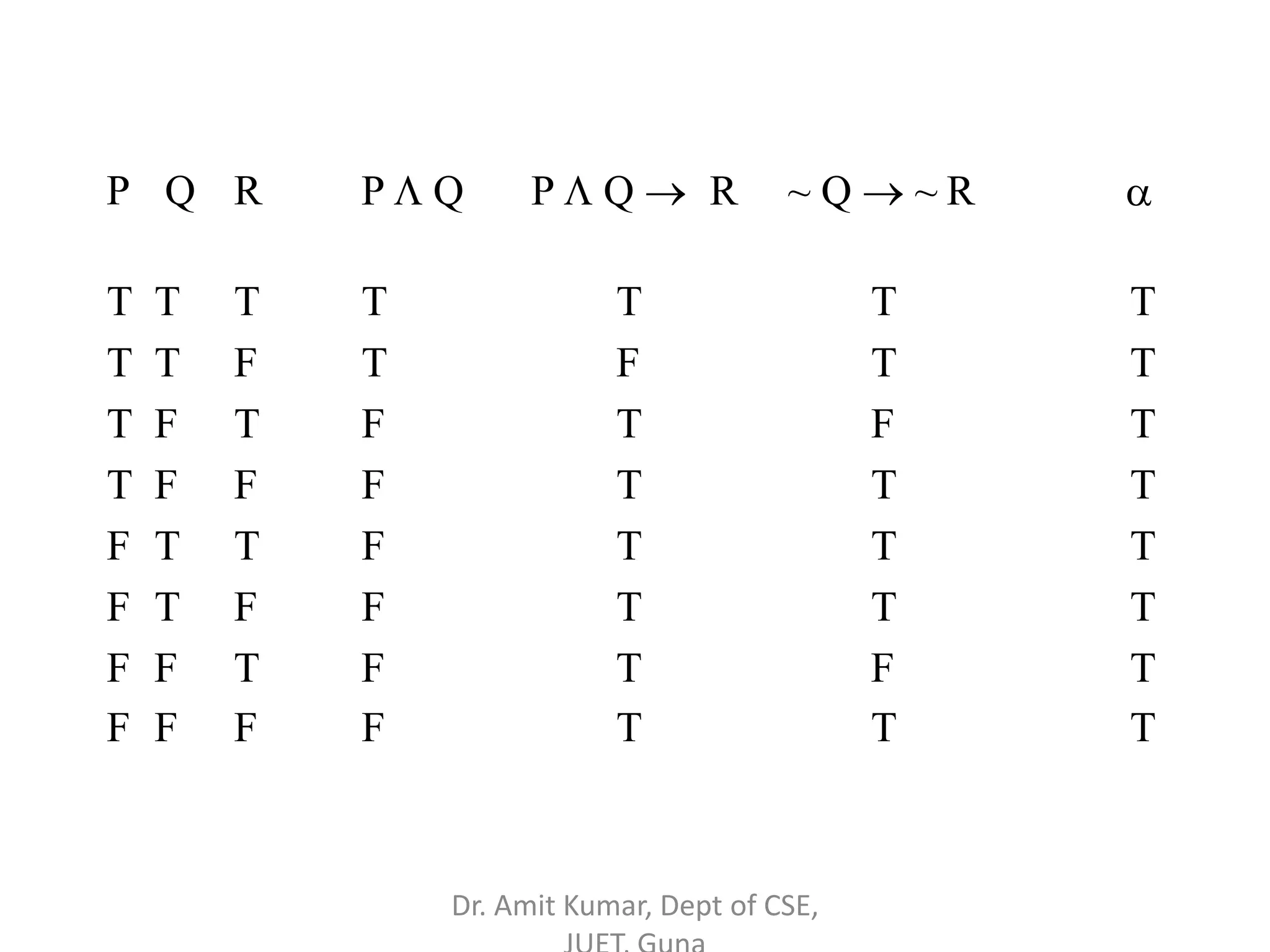
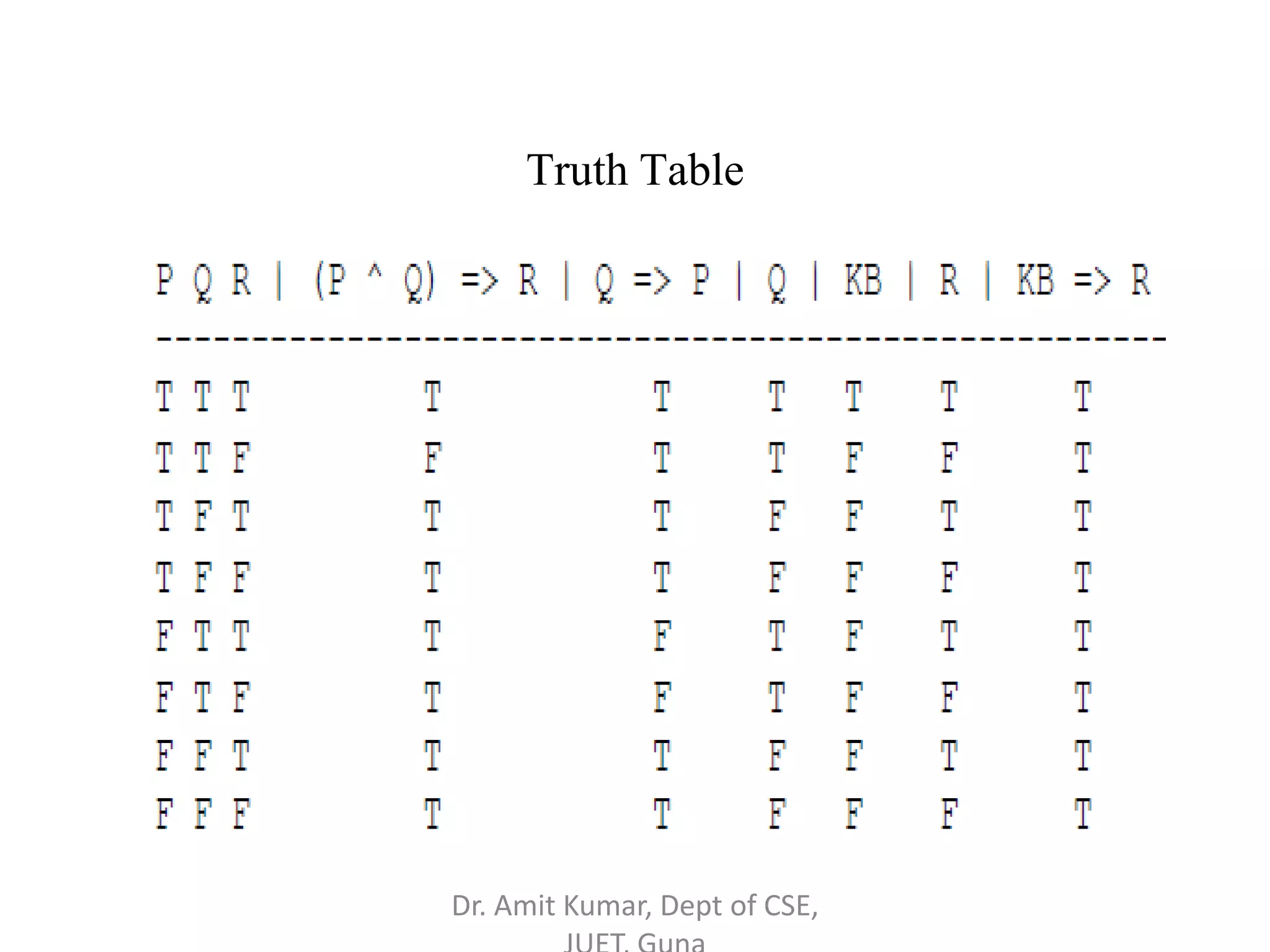
- Truth tables are used to determine the truth values of propositional statements under different variable assignments. Various rules of inference like modus ponens are discussed.
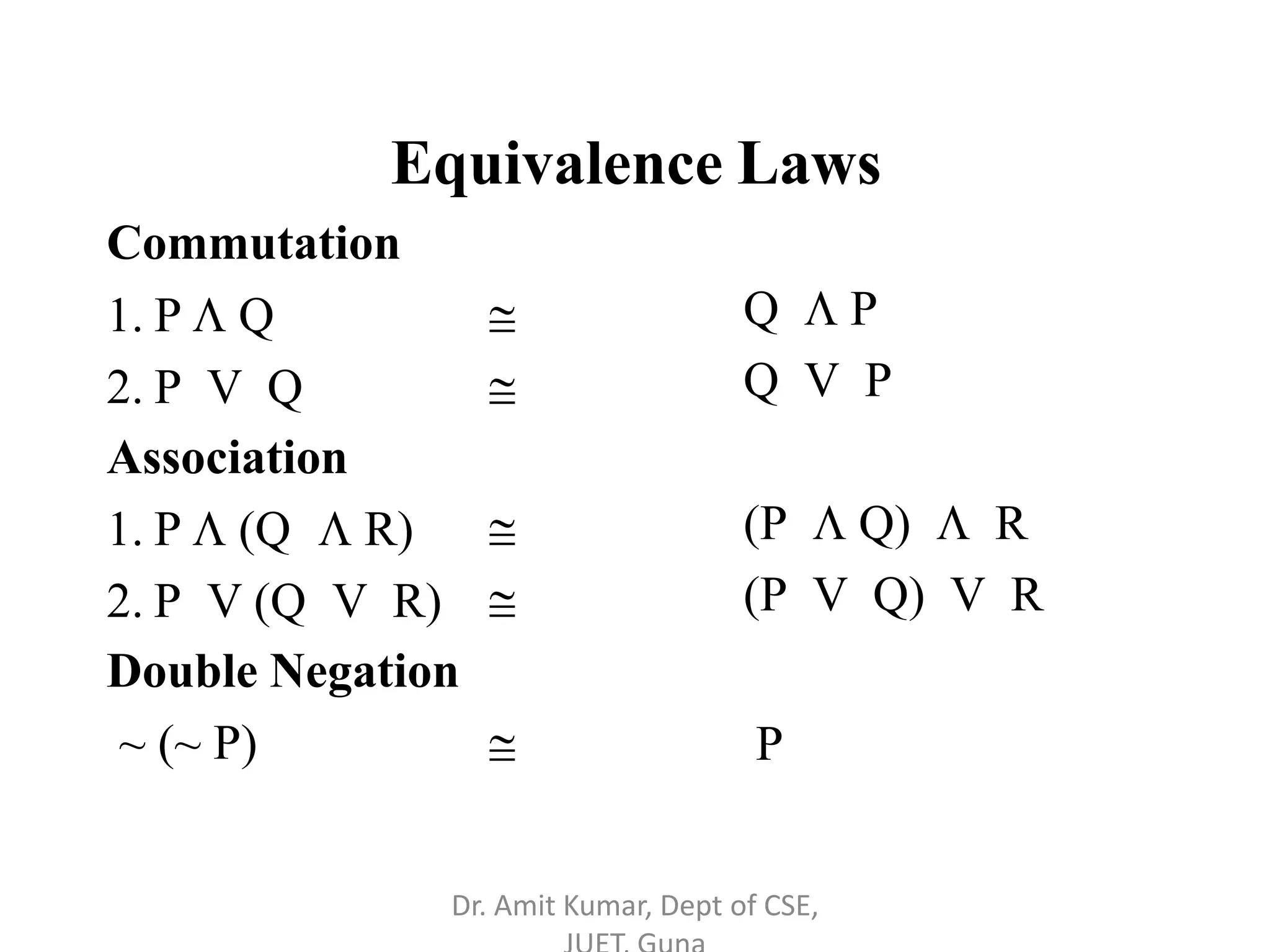
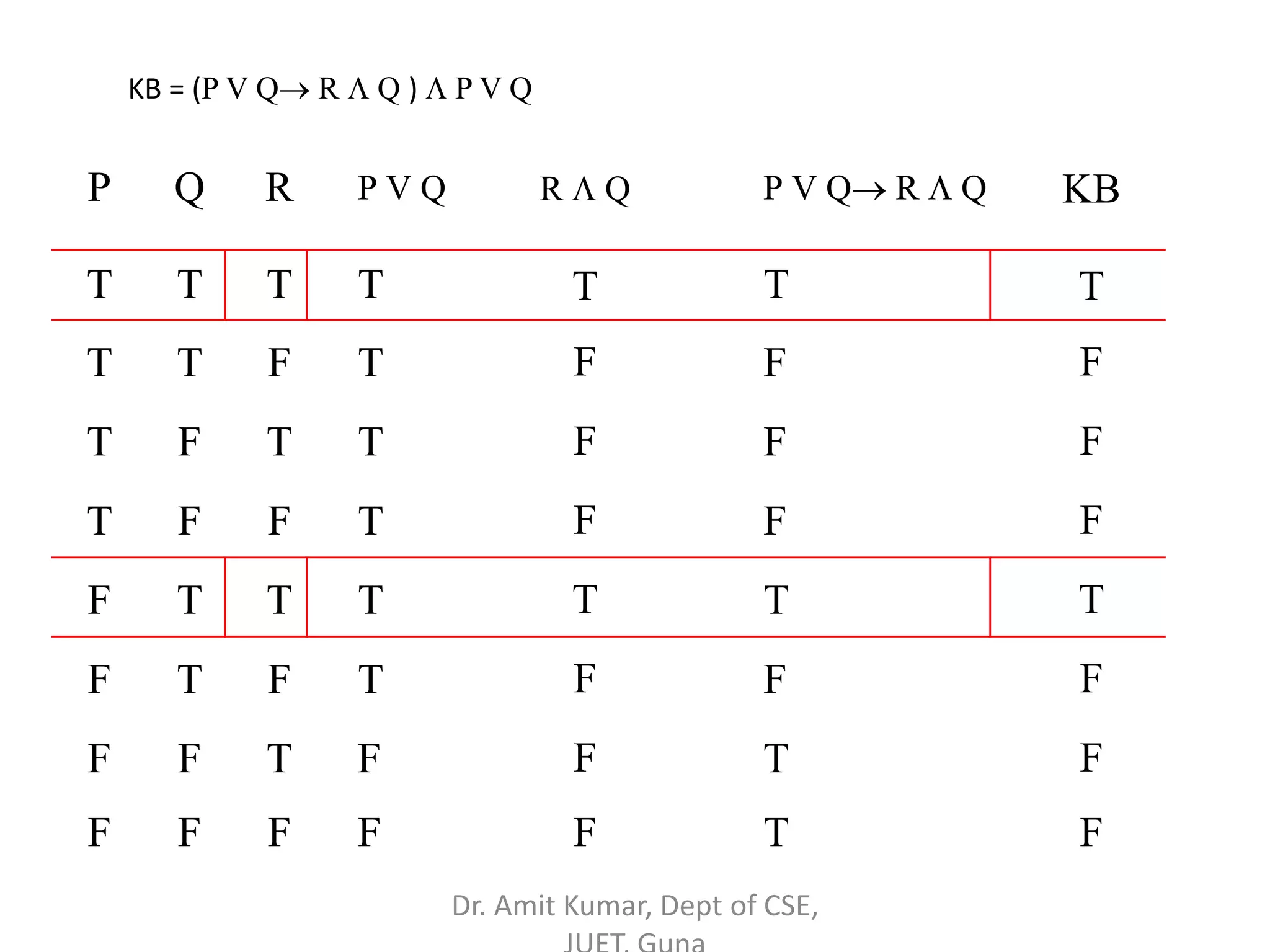
- Propositional logic deals with validity, satisfiability, and logical consequence through truth table analysis and the application of equivalence laws. Examples are provided to illustrate logical reasoning techniques.

































![•We use notation I[α] = T (or F), which means that α is
evaluated to be true or false under interpretation I over a
domain D.
•Let α and β are formulae and I be an interpretation over any
domain D. The following holds true.
•I[αΛβ] = I[α] ΛI[β]
•I[αV β] = I[α] V I[β]
•I[α→β] = I[α] →I[β]
•I[~α] = ~ I[α]
= T if and only if I[α] = F
•For any interpretation I and formulae using (∀x) and (∃x),
the following results holds true.
•I[(∀x)P(x)] = T iff I[P(x)] = T, ∀x ∈D
= F, otherwise
•I[(∃x) P(x)] = T iff ∃c∈D such that I[P(c)] = T
= F, otherwise
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-39-2048.jpg)
![•A formula α is said to be consistent (satisfiable) if and only if
there exists an interpretation I such that I[α] = T. Alternatively we
say that I is a model of α or I satisfies α.
•A formula α is said to be inconsistent(unsatisfiable) if and only
if ∃no interpretation that satisfies αor there exists no model for α.
•A formula α is valid if and only if for every interpretation I, I[α] =
T.
•A formula α is a logical consequence of a set of formulae {α1,
α2, ..., αn} if and only if for every interpretation I, if I[α1Λ…Λαn]
= T, then I[α] = T.
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-40-2048.jpg)







![Isa relationship
1. Isa predicate is used to show subclass-superclass relationship.
2. The implication rule in sentence 3 states that if an object is an instance of
the subclass Pompeian then it is an instance of the superclass Roman.
1. Instance(Marcus,man)
2. Instance(Marcus, Pompeian)
3. Isa(Pompeian, Roman)
4. Instance( Caesar, ruler)
5. ∀ x: Instance(x,Roman) loyalto(x, Caesar) V hate(x, Caesar)
6. ∀ x: ∀ y: ∀ z: Instance( x, y) Λ isa(y,z) Instance( x, z)
In logical representation, it is difficult to define overriding property
Suppose, for example, that, in addition to the facts we already have, we add the
following:
Pompeian(Paulus)
~ [loyalto(Paulus, Caesar) V hate(Paulus, Caesar)]
•In other words, suppose we want to make Paulus an exception to the general rule
about Romans and their feelings toward Caesar.
•Unfortunately, we cannot simply add these facts to our existing knowledge base.
•The difficulty is that if the old assertions are left unchanged, then the addition of
the new assertions makes the knowledge base inconsistent. So our original
sentence 5 must become
1. ∀ x : Roman(x) Λ ~eq(x, Paulus) loyalto(x, Caesar) V hate(x, Caesar)
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-48-2048.jpg)

![Computable Functions example
Original facts given as:
1. man(Marcus)
2. Pompeian(Marcus)
3. Marcus was born in 40 A.D. : born(Marcus, 40)
4. All men are mortal. ∀ x : man(x) mortal(x)
All Pompeians died when the volcano erupted in 79 A.D.
erupted(volcano, 79) Λ ∀ x : [Pompeian(x) died(x, 79)] can be written as
5. ∀ x : [Pompeian(x) died(x, 79)] 6. erupted(volcano, 79)
7. No mortal lives longer than 150 years.
∀ x: ∀ t1 : ∀ t2 : mortal(x) Λ born(x, t1) Λ gt(t2-t1,150) dead(x, t2)
Or ∀ x: mortal(x) Λ gt(age(x), 150) dead(x)
8. It is now 1991. now = 1991
Additional Fact: added later
9. Alive means not dead. ∀ x : ∀ t : [alive(x,t) ~dead(x,t)] Λ [~dead(x,t) alive(x,t)
10. If someone dies, then he is dead at all later times.
∀ x: ∀ t1 : ∀ t2 : died(x,t1) Λ gt(t2, t1) dead(x, t2)
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-50-2048.jpg)



![Conversion to Clause Form
1. Eliminate , using the fact that a b is equivalent to ~ a V b. Performing this
transformation on the following wff for fact :
All the roman who knows marcus either hate caesar or think that anyone who hates anyone
is crazy Wff
∀ x: [Roman(x) Λ know(x, Marcus)] [hate(x, Caesar) V
(∀ y : (∃z : hate(y, z)) thinkcrazy(x,y))]
Clause form
∀ x: ~ [Roman(x) Λ know(x, Marcus)] V [hate(x, Caesar) V
(∀ y : ~(∃z : hate(y, z)) V thinkcrazy(x,y))]
2. Reduce the scope of each ~ to a single term, using the fact that ~ (~ p) = p,
deMorgan's laws [which say that
~(a Λ b) = ~ a V ~b and ~(a V b) = ~ a Λ ~ b], and
the standard correspondences between quantifiers
[~∀ x : P(x) = ∃ x : ~P(x) and ~ ∃ x : P(x) = ∀ x : ~ P(x)].
Performing this transformation on the wff from step 1 yields
∀ x: [~Roman(x) V ~know(x, Marcus)] V [hate(x, Caesar) V
(∀ y : ∀ z : ~hate(y, z) V thinkcrazy(x,y))]
For equivalence relationship use formula: P ↔Q ≅( P →Q) Λ( Q →P)
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-54-2048.jpg)
![3. Standardize variables so that each quantifier binds a unique variable. Since
variables are just dummy names, this process cannot affect the truth-value of
the wff. For example, the formula
∀ x : P(x) V ∀ x : Q(x)
would be converted to
∀ x: P(x1) V ∀ x2 : Q(x2)
4. Move all quantifiers to the left of the formula without changing their relative
order. This is possible since there is no conflict among variable names.
Performing this operation on the formula of step 2, we get
∀ x: ∀ y : ∀ z : [~Roman(x) V ~know(x, Marcus)] V [hate(x, Caesar) V
(~hate(y, z) V thinkcrazy(x,y))]
At this point, the formula is in what is known as prenex normal form. It consists of a
prefix of quantifiers followed by a matrix, which is quantifier free.
5. Eliminate existential quantifiers. A formula that contains an existentially
quantified variable asserts that there is a value that can be substituted for the
variable that makes the formula true. We can eliminate the quantifier by
substituting for the variable a reference to a function
∃ y : President(y) can be transformed into the formula President(S1)
where S1 is a function with no arguments that somehow produces a value that
satisfies President. Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-55-2048.jpg)
![If existential quantifiers occur within the scope of universal quantifiers, then the value
that satisfies the predicate may depend on the values of the universally quantified
variables. For example, in the formula
∀ x: ∃ y: father-of(y,x)
the value of y that satisfies father-of depends on the particular value of x. Thus we
must generate functions with the same number of arguments as the number of
universal quantifiers in whose scope the expression occurs. So this example would be
transformed into
∀ x :father-of(S2(x),x))
These generated functions are called Skolem functions. Sometimes ones with no
arguments are called Skolem constants.
6. Drop the prefix. At this point, all remaining variables are universally quantified, so
the prefix can just be dropped
[~Roman(x) V ~know(x, Marcus)] V [hate(x, Caesar) V (~hate(y, z) V thinkcrazy(x,y))]
7. Convert the matrix into a conjunction of disjuncts. In the case of our
example, since there are no and's (i.e. Λ ), it is only necessary to exploit the
associative property of or(i.e. V) [i.e., a V (b V c) = (a V b) V c] and simply
remove the parentheses, giving
~Roman(x) V ~know(x, Marcus) V hate(x, Caesar) V ~hate(y, z) V thinkcrazy(x,y)
Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-56-2048.jpg)
![However, it is also frequently necessary to exploit the distributive property
[i.e., (a Λ b) V c = (a V c) Λ (b V c)]
For example, the formula
(winterΛ wearingboots) V (summerΛ wearingsandals)
becomes, after one application of the rule
[winter V (summerΛ wearingsandals)] Λ
[wearingboots V (summerΛwearingsandals)]
and then, after a second application.
(winter V summer) Λ
(winter V wearing sandals) Λ
(wearingboots V summer) Λ
(wearingboots V wearingsandals)
9. Create a separate clause corresponding to each conjunct. In order for a wff to be true,
all the clauses that are generated from it must be true. If we are going to be working
with several wff's, all the clauses generated by each of them can now be combined to
represent the same set of facts as were represented by the original wff's.
10. Standardize apart the variables in the set of clauses generated in step 8. By this we
mean rename the variables so that no two clauses make reference to the same
variable. In making this transformation, we rely on the fact that
(∀ x : P(x) Λ Q(x)) = ∀ x : P(x) Λ ∀ x : Q(x)Dr. Amit Kumar, Dept of CSE,](https://image.slidesharecdn.com/logic-180428060612/75/Logic-57-2048.jpg)