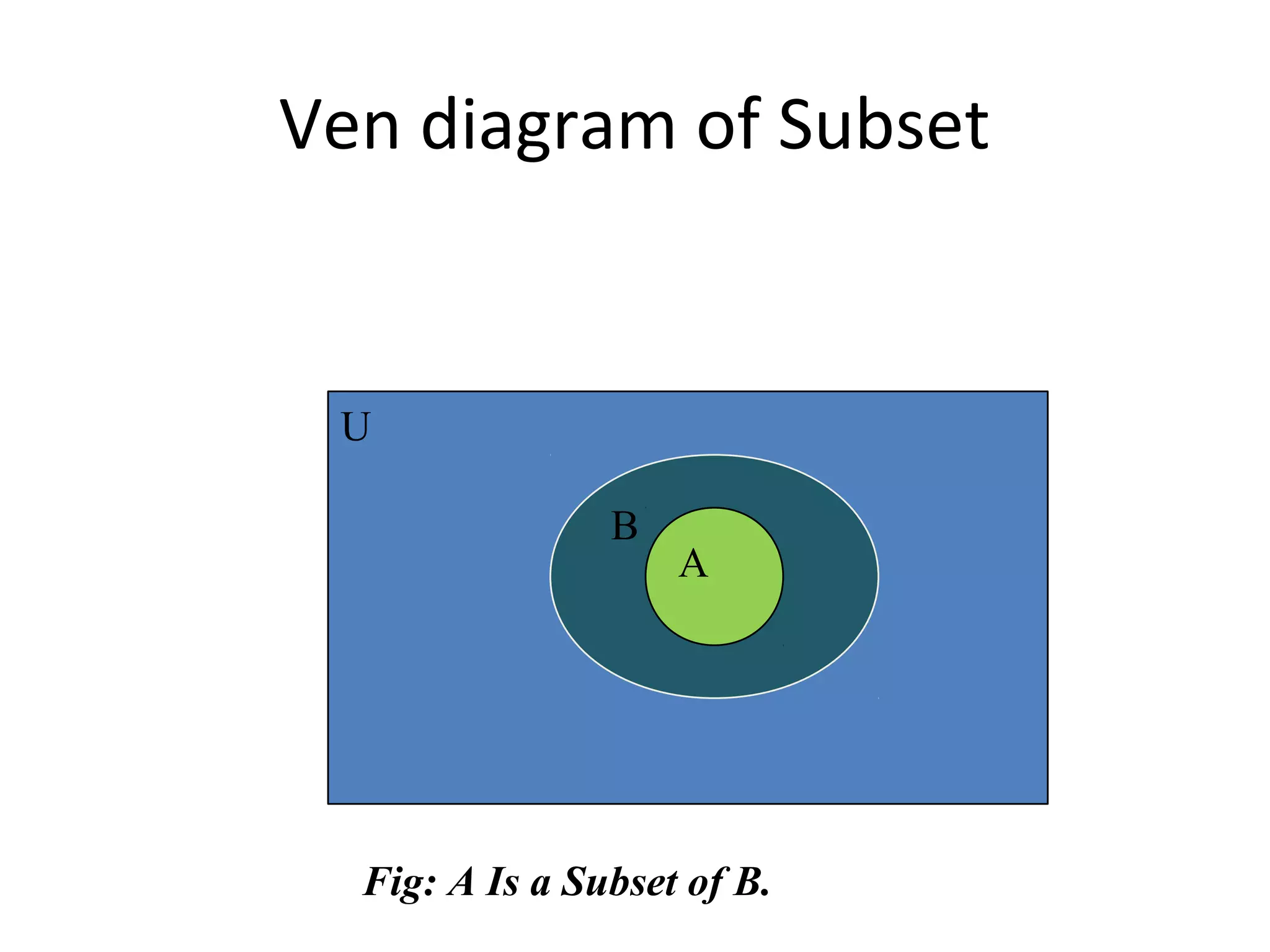
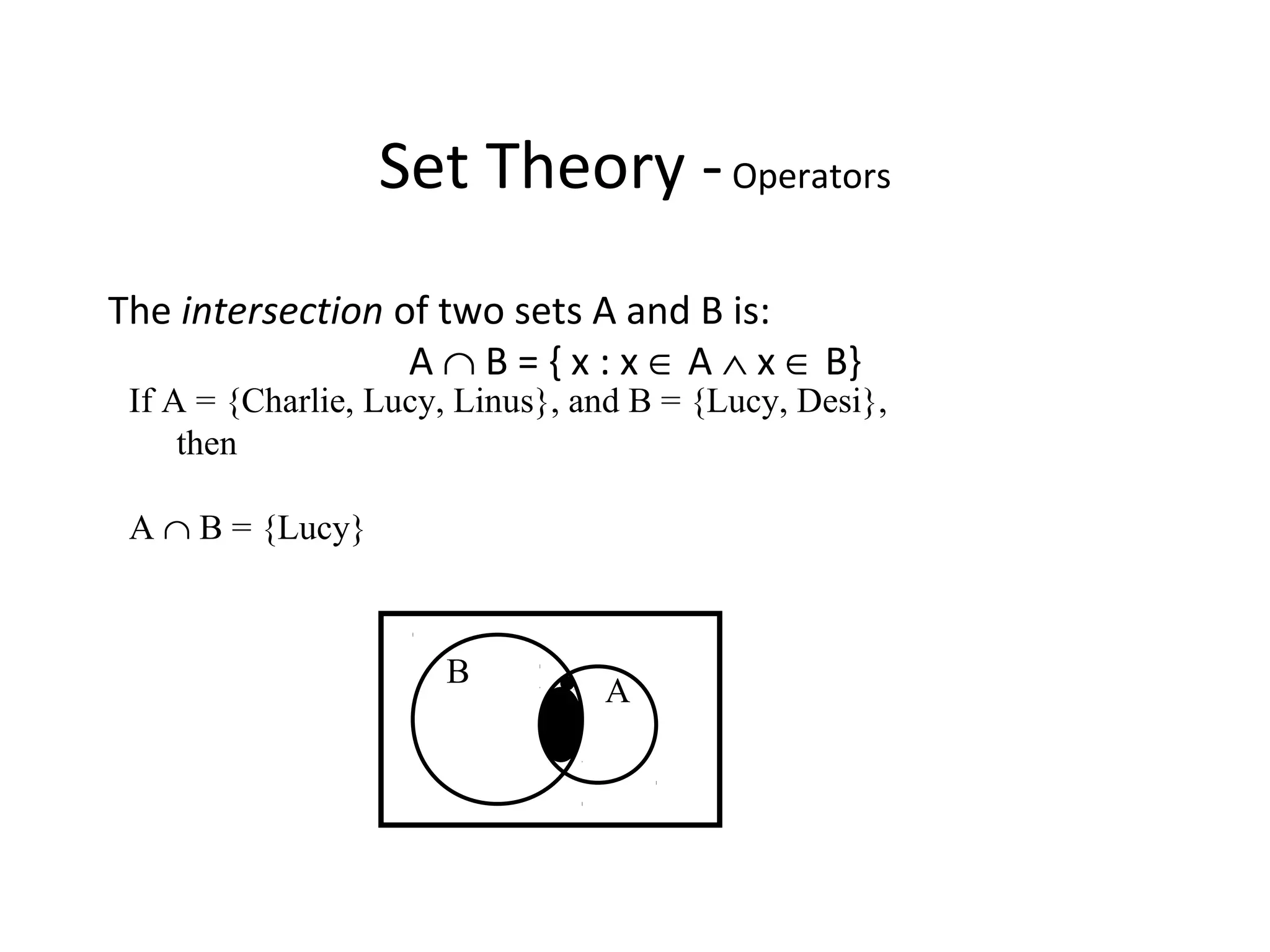
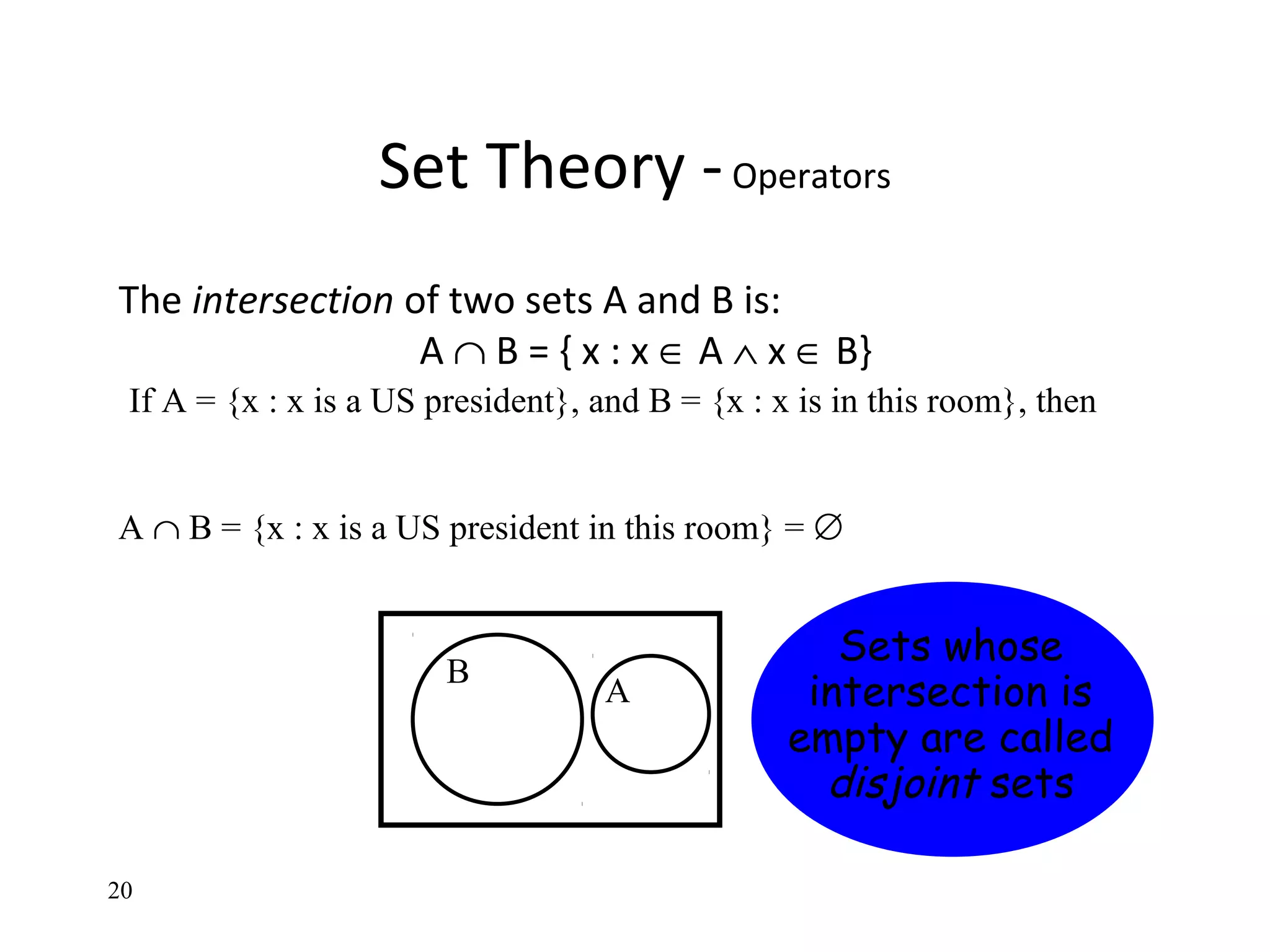
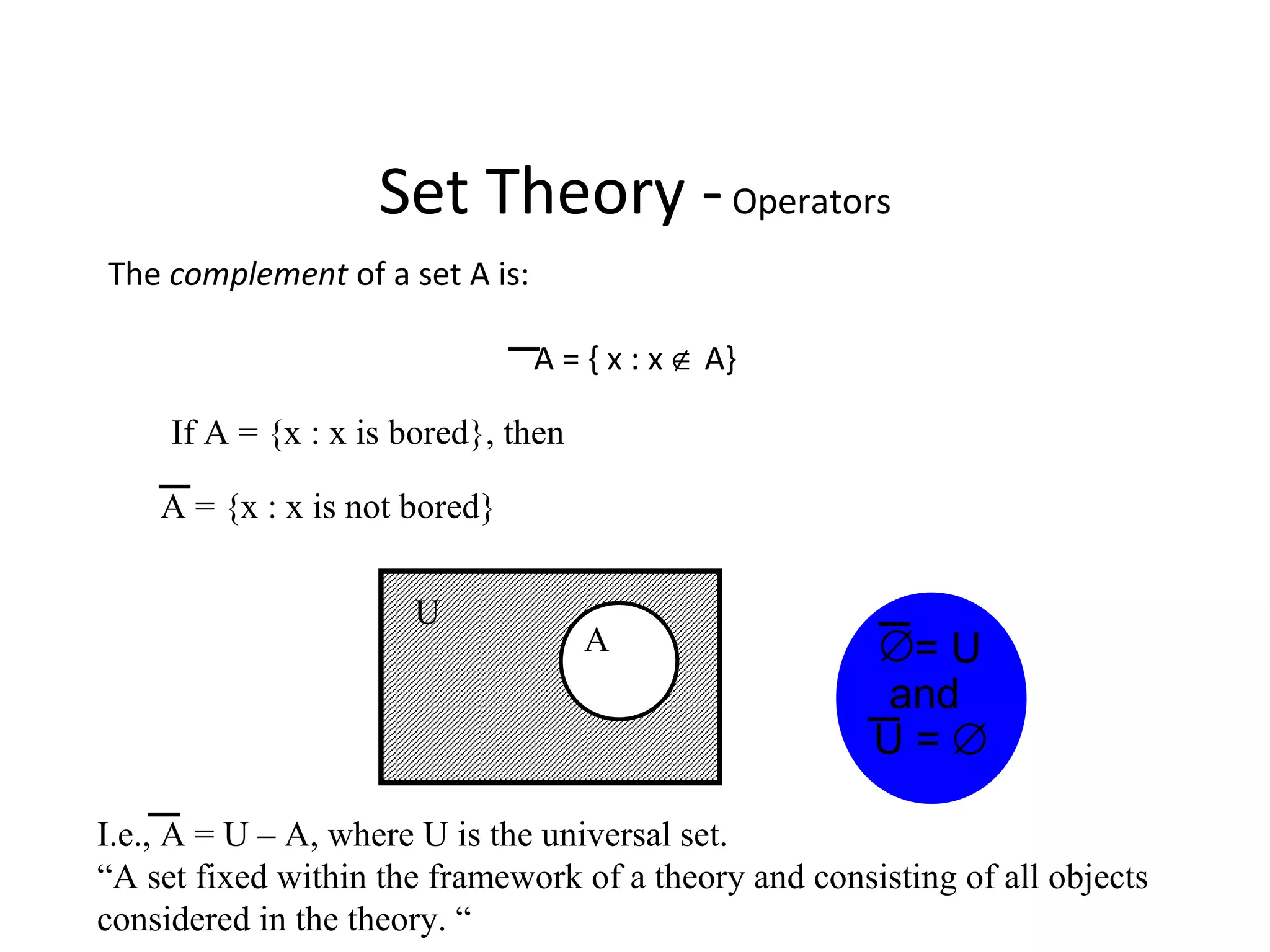
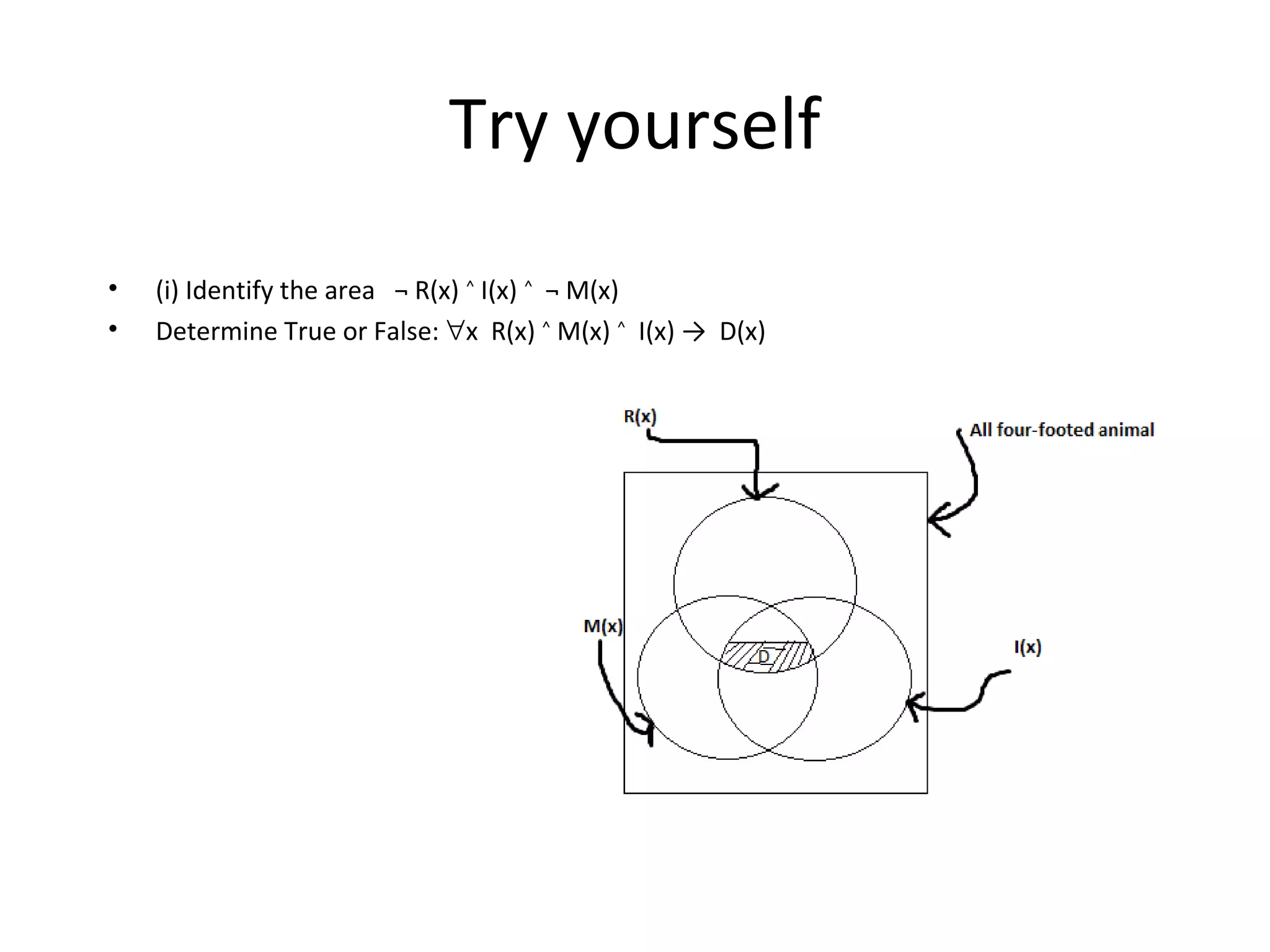
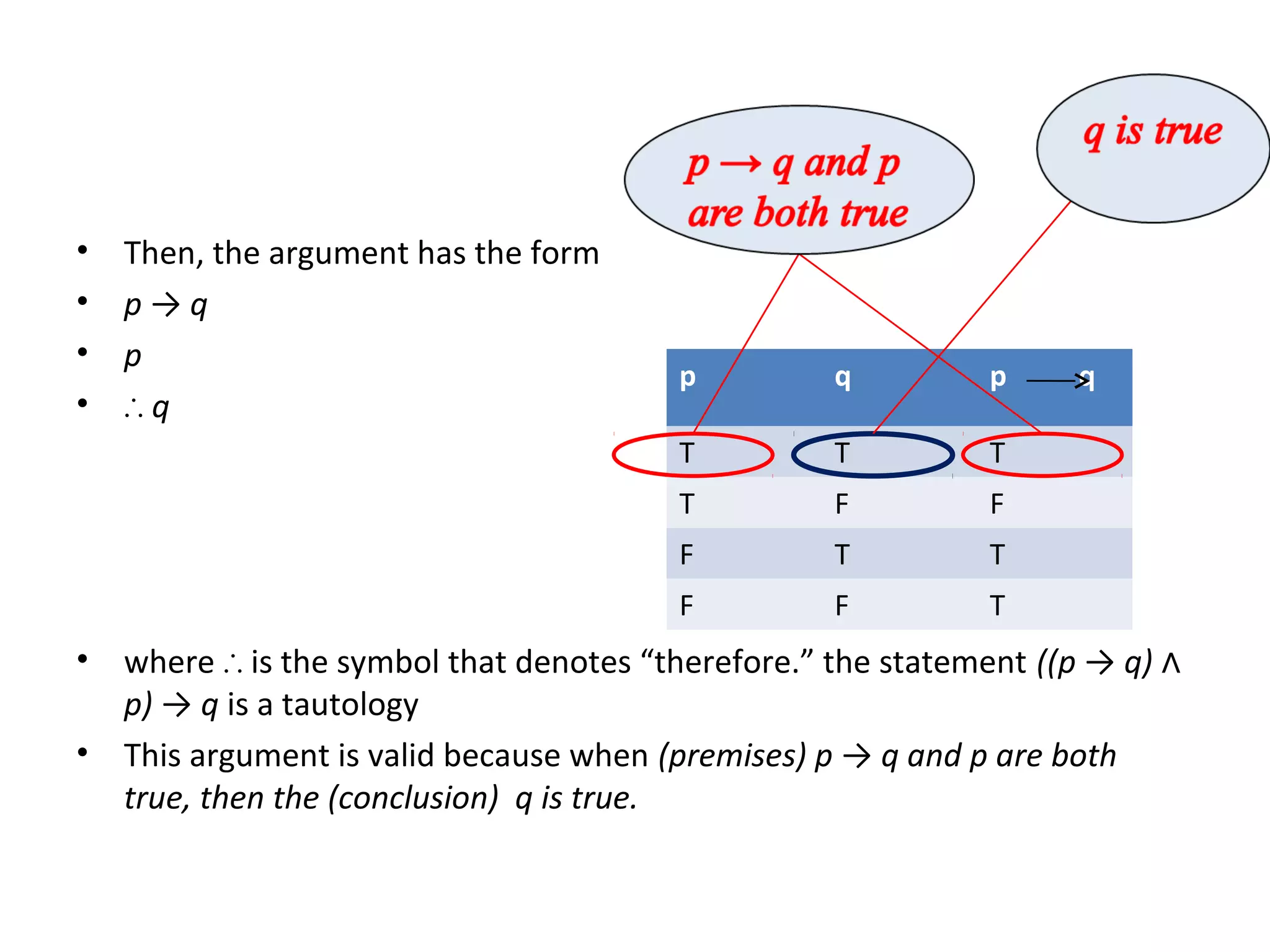
The document provides an overview of sets in discrete mathematics, detailing their definitions, properties, and notations. It covers concepts such as subsets, power sets, set operations (union, intersection, complement), and the concept of the empty set. Additionally, it includes examples and exercises to illustrate these concepts.