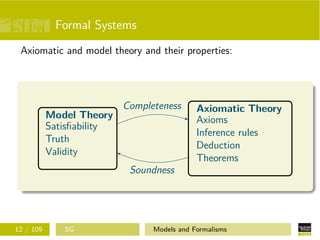
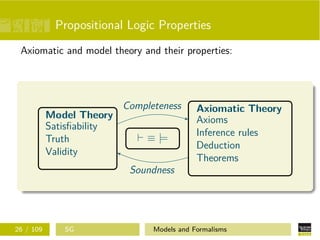
The document discusses models and formalisms in logic. It introduces formal systems as consisting of an axiomatic theory, symbols for constructing formulas, grammar rules, axioms, inference rules, and properties like consistency. Propositional and predicate logic are examined, including their model theories, axiomatic theories, properties like completeness and soundness, and resolution principles. Normal forms and the resolution rule are defined as ways to deduce theorems in a formal system.

1. Models and Formalisms
S. Garlatti
MR2A Informatique
2012

2. Progress
1 Introduction
2 Formal Systems
3 Propositional Logic
4 The Predicate Calculus or First Order Logic
2 / 109 SG Models and Formalisms

3. Introduction
Concatenation Modeling?
Answer from a logical point of view:
Conc([X|L], L1, [X|L2]) :− Conc(L, L1, L2).
Conc([], L, L).
Conc([a,b], [c,d], L)?
3 / 109 SG Models and Formalisms

4. Introduction
History of Logic
Plato’s logic, Aristotle’s logic, Stoic logic
Medieval logic, etc.
Rise of Modern Logic, the mid-nineteenth century:
Rigorous and formalistic discipline whose exemplar was the exact
method of proof used in mathematics
The modern so-called "symbolic" or "mathematical" logic
Modern logic: a calculus whose rules of operation are determined
only by the shape and not by the meaning of the symbols it
employs, as in mathematics.
4 / 109 SG Models and Formalisms

5. Progress
1 Introduction
2 Formal Systems
3 Propositional Logic
4 The Predicate Calculus or First Order Logic
5 / 109 SG Models and Formalisms

6. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
6 / 109 SG Models and Formalisms

7. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
6 / 109 SG Models and Formalisms

8. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
A grammar to define well-formed formulas (abbreviated wff ).
6 / 109 SG Models and Formalisms

9. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
A grammar to define well-formed formulas (abbreviated wff ).
A set of Axioms or axiom schemata: each axiom must be a wff .
6 / 109 SG Models and Formalisms

10. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
A grammar to define well-formed formulas (abbreviated wff ).
A set of Axioms or axiom schemata: each axiom must be a wff .
A set of Inference rules
6 / 109 SG Models and Formalisms

11. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
A grammar to define well-formed formulas (abbreviated wff ).
A set of Axioms or axiom schemata: each axiom must be a wff .
A set of Inference rules
From Axioms and Inferences Rules, Theorems are deduced.
6 / 109 SG Models and Formalisms

12. Formal Systems
Formal Systems (or Formalism) consist of :
An Axiomatic Theory
A finite set of symbols for constructing formulas.
A grammar to define well-formed formulas (abbreviated wff ).
A set of Axioms or axiom schemata: each axiom must be a wff .
A set of Inference rules
From Axioms and Inferences Rules, Theorems are deduced.
Properties: Consistency and Decidability
6 / 109 SG Models and Formalisms

13. Formal Systems
The Formal Systems MIU, Axiomatic Theory
Alphabet A = {M, I, U}.
A grammar : wff consist of all series of the three alphabet
elements.
A set of axioms= {MI}.
A set of inference rules: Let f , g variables representing wff , g
could be empty
R1: f fU
R2: Mf Mff
R3: fIIIg fUg
R4: fUUg fg
7 / 109 SG Models and Formalisms

14. Formal Systems
The Formal Systems MIU, Axiomatic Theory
Some Theorems:
R2: MI MII
R1: MII MIIU
R1: MIIU MIIUU
R4: MIIUU MII
R2: MII MIIII
R3: MIIII MIU
MU is a theorem?
8 / 109 SG Models and Formalisms

15. Formal Systems
Formal Systems consist of : A Model Theory or Semantics
A standard model M:
It is a structure that gives a concrete interpretation of the theory
(axiomatic theory).
For instance, M = (D, I)
D is the interpretation domain.
An Interpretation function I that assigns:
- Let A a set of alphabet elements, (A)I
: A → D
- Let F a set of wff , (F)I
: F → {True, False}
Properties: consistency, soundness, completeness
9 / 109 SG Models and Formalisms

16. Formal Systems
The Axiomatic Theory of Formal Systems pg
Alphabet A = {p, g, −}
wff all series of p, g, −
x ∈ {−, −−, ..., −n
}, Axiom Schema:
xp − gx−
x, y, z ∈ {−, −−, ..., −n
},Inference Rules :
xpygz xpy − gz−
10 / 109 SG Models and Formalisms

17. Formal Systems
The Model Theory of the formal system pg
An Interpretation function I that assigns:
(p)I : plus, (g)I : equal, (−n)I : n
(− − −p − −g − − − −−) ⇒ (3 plus 2 equal 5) ⇒
(− − −p − −g − − − −)I = True
(− − −p − g − − − −−) ⇒ (3 plus 1 equal 5) ⇒
(− − −p − g − − − −−)I = False
11 / 109 SG Models and Formalisms

18. Formal Systems
Axiomatic and model theory and their properties:
Model Theory
Satisfiability
Truth
Validity
Axiomatic Theory
Axioms
Inference rules
Deduction
Theorems
Completeness
Soundness
12 / 109 SG Models and Formalisms

19. Progress
1 Introduction
2 Formal Systems
3 Propositional Logic
4 The Predicate Calculus or First Order Logic
13 / 109 SG Models and Formalisms

20. The Propositional Logic
The Language and the well-formed formulae or wff
A set of propositional symbols S
A set of connectors: ¬, →, ↔, ∨, ∧
Let p, q, r ∈ S, p, q, r are atoms
An atom is a wff , then p, q, r are wff
Let P be a wff , then ¬P is a wff
Let P, Q be wff , then (P → Q), (P ↔ Q), (P ∨ Q), (P ∧ Q)
All wff are generated by applying the above rules
14 / 109 SG Models and Formalisms

21. The Model Theory of Propositional Logic
In Propositional logic, I is an Interpretation function that assigns:
A truth value in {T, F}, to an atom or a well-formed formula,
Let P, Q be wff , assignment of Truth Values are made as follows:
P Q ¬P (P ∧ Q) (P ∨ Q) (P → Q)
T T F T T T
T F F F T F
F T T F T T
F F T F F T
The Interpretation function I is truth-functional: the truth or
falsity of a well-formed formula is determined by the truth or falsity
of its components.
15 / 109 SG Models and Formalisms

22. Truth, Validity
A wff P is said to be True under an interpretation I iff P is
evaluated to T in the interpretation;
Otherwise, P is said to be False under the interpretation.
A wff is said to be Valid iff it is true under all its interpretations
A wff is said to be Inconsistent or Unsatisfiable iff it is false
under all its interpretations
A wff is said to be Consistent or Satisfiable iff it is not
Inconsistent
16 / 109 SG Models and Formalisms

23. Truth, Validity
Examples of Valid or inconsistent formulae
(P ∧ ¬P)
(P → P)
((P ∧ ¬P) → Q)
(P ∨ ¬P)
17 / 109 SG Models and Formalisms

24. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
18 / 109 SG Models and Formalisms

25. Axiomatic Theory
An axiomatic theory is composed of:
A language and wff
A set of axioms
Inference rules
19 / 109 SG Models and Formalisms

26. Axioms
Let P, Q, R be wff
A1 : (P → (Q → P))
A2 : (P → (Q → R)) → ((P → Q) → (P → R)))
A3 : (¬P → ¬Q) → ((¬P → Q) → P))
One inference rule
Modus Ponens: P, (P → Q) Q
From hypothesis P and (P → Q), Q is deduced
20 / 109 SG Models and Formalisms

27. Deduction
Theorem demonstration: (A → A)
A1 : (A → ((A → A) → A))
A2 : ((A → ((A → A) → A)) →
((A → (A → A) → (A → A))))
A1, A2 ((A → (A → A)) → (A → A))
A1” : (A → (A → A))
A1”, ((A → (A → A)) → (A → A)) (A → A)
(A → A)
21 / 109 SG Models and Formalisms

28. Deduction
Theorem demonstration: (A → A)
A1 : (A → ((A → A) → A))
A2 : ((A → ((A → A) → A)) → ((A → (A → A) → (A → A))))
((A → (A → A)) → (A → A))
A1” : (A → (A → A)) ((A → (A → A)) → (A → A))
(A → A)
22 / 109 SG Models and Formalisms

29. Theorems
Some theorems
The law of noncontradiction: ¬(P ∧ ¬P)
Or ((P ∧ ¬P) → Q)
The law excluded middle: (P ∨ ¬P)
23 / 109 SG Models and Formalisms

30. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
24 / 109 SG Models and Formalisms

31. Propositional Logic Properties
Completeness Theorem
Every Valid formula of the predicate calculus is a theorem.
- if |= F then F
Soundness Theorem
Every theorem of the predicate calculus is a Valid formula
- if F then |= F
The propositional Logic is decidable
25 / 109 SG Models and Formalisms

32. Propositional Logic Properties
Axiomatic and model theory and their properties:
Model Theory
Satisfiability
Truth
Validity
Axiomatic Theory
Axioms
Inference rules
Deduction
Theorems
≡ |=
Completeness
Soundness
26 / 109 SG Models and Formalisms

33. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
27 / 109 SG Models and Formalisms

34. Resolution Principles
Normal Forms
Definition: A Literal is an atomic formula or Atom or the
negation of an Atom
A Formula F is called a Clause if and only if F is composed of a
disjunction of literals, (F1 ∨ F2, ... ∨ Fn), n 1
An empty clause, denoted , is unsatisfiable or always
interpreted as False, (deduced from the conjunction of two
complementary literals P and ¬P)
28 / 109 SG Models and Formalisms

35. Resolution Principles
Normal Forms
Definition: A formula F is in a Conjunctive Normal Form if
and only if F has the following form (F1 ∧ F2, ... ∧ Fn), n 1,
where each of F1, F2, ..., Fn is a disjunction of literals or a clause.
Any formula can be transformed into a normal forms
29 / 109 SG Models and Formalisms

36. Resolution Principles
One possible resolution rule: the Cut Elimination Rule of
Gentzen
Let D and E be clauses without any occurrence of literals P or
¬P
(¬P ∨ E), (P ∨ D) (E ∨ D)
The clause (E ∨ D) is called the resolvent
This rule is a generalization of the Modus Ponens Rule (obtained
by elimination of the clause D)
30 / 109 SG Models and Formalisms

37. Resolution Principles
Let F be a set of clauses and A be a clause
To demonstrate F A
By means of the Cut Elimination Rule, the goal is to show that
{F, ¬A} is unsatisfiable.
It is a refutation
Demonstration of the unsatisfiability of {F, ¬A}
Obtain a resolvent equal to the empty clause , by elimination
of complementary literals in two different clauses.
31 / 109 SG Models and Formalisms

38. Resolution Principles
Example : let F be a conjunctive normal form as follows:
F = ((P ∨ Q) ∧ (¬P ∨ Q) ∧ (P ∨ ¬Q) ∧ (¬P ∨ ¬Q))
F unsatisfiable?
(P ∨ Q) (¬P ∨ Q)
Q
(P ∨ ¬Q) (¬P ∨ ¬Q)
¬Q
32 / 109 SG Models and Formalisms

39. Progress
1 Introduction
2 Formal Systems
3 Propositional Logic
4 The Predicate Calculus or First Order Logic
33 / 109 SG Models and Formalisms

40. The Predicate Calculus
Predicate calculus (first-order logic): an extension of the
propositional logic
The Language
A set of Constants C
A set of Variables V
A set of function symbols F
A set of Terms T
A set of predicate symbols P
A set of connectors: ¬, →, ↔, ∨, ∧
A set of Quantifiers: ∀, ∃
34 / 109 SG Models and Formalisms

41. The Language
The Terms
A Constant a is a term
A Variable x is a term
if t1, t2, ..., tn ∈ T, (n > 0), then f (t1, t2, .., tn) ∈ T
where f is a function symbol of arity n.
Well-Formed Formula or wff
If P is a predicate symbol and if t1, t2, . . . , tn ∈ T(n > 0) then
P(t1, t2, ..., tn) is an atomic formula
If G and H are wff then
(G → H), (G ↔ H), (G ∨ H), (G ∧ H), ¬G, ∀xG(x) and ∃xG(x)
are wff .
35 / 109 SG Models and Formalisms

42. The Language
Quantification theory
Scope of quantifiers
Free and bound variables
Examples of wff :
∀x∃y(P(x, a, f (y), z) → ∀yQ(y, g(x, a)))
(P(x, f (z)) ∨ ∀xQ(x, z))
∀z(∃yP(y, b) ∧ Q(y, f (a, z))
36 / 109 SG Models and Formalisms

43. The Language
Quantification theory
∀x∃y(P(x, a, f (y), z) → ∀yQ(y, g(x, a)))
x, y are bound variables, z is a free variable, the second variable y
is bound to the quantification forally, a is a constant, f and g are
functional symbols.
(P(x, f (z)) ∨ ∀xQ(x, z))
the first occurrence of x is free, the second is bound, the two
occurrences of z are free, but they do not represent the same
variable.
∀z(∃yP(y, b) ∧ Q(y, f (a, z))
The second occurrence of y is free, the first one bound, z is bound.
37 / 109 SG Models and Formalisms

44. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
38 / 109 SG Models and Formalisms

45. Standard Model
A standard model is a structure M = (D, I) Where
D is a nonempty set called the Interpretation Domain
I is an Interpretation function that assigns:
A truth value in {T, F}, to a well-formed formula,
A n-place relation to a nary predicate symbol,
An n-place operation to a nary function symbol
An element of D to a constant
An element of D to variable
An element of D to a nary functional term
The interpretation function I is also Truth-Functional
39 / 109 SG Models and Formalisms

46. Satisfiability, Truth, Models, Validity
Let s be a denumerable sequence of D elements, s = (s1, s2, ..., sn)
The idea is: from a sequence s, the corresponding n-tuple
< s1, s2, ..., sn > will satisfy a wff F with free variables
(x1, x2, ..., xn)
For instance, the sequence s = (s1, s2, ..., sn) of elements of the
Domain D will satisfy the wff F(x2, x5)
if the ordered pair < s2, s5 > is in the relation (F)I
assigned to
the predicate symbol F by the interpretation I.
40 / 109 SG Models and Formalisms

47. Satisfiability, Truth, Models, Validity
An Interpretation I:
a ∈ C, (a)I
: C → D
x ∈ V , (x)I
: V → D
t1, t2, . . . , tn and f (t1, t2, .., tn) are terms, f ∈ F,
(f (t1, t2, .., tn))I : Dn → D
with (f (t1, t2, .., tn))I ≡ ((f )I((t1)I, (t2)I, .., (tn)I))
if ti is the variable xi , (t)I is equal to the sequence element si
41 / 109 SG Models and Formalisms

48. Satisfiability, Truth, Models, Validity
Satisfiability
If F(t1, t2, .., tn) is an atomic formula and (F)I
is the
corresponding n-place relation then the sequence
s = (s1, s2, ..., sn) satisfies F(t1, t2, .., tn) if and only if
(F)I
((t1)I
, (t2)I
, .., (tn)I
)), that is to say the n-tuple
< s1, s2, ..., sn > is in (or verify) the relation (F)I
.
s satisfies ¬F if and only if s does not satisfies F
s satisfies (F → G) if and only if s does not satisfy F or s
satisfies G
s satisfies ∀xi F if and only if every sequence s that differs from s
in at most the ith
component satisfies F
42 / 109 SG Models and Formalisms

49. Satisfiability, Truth, Models, Validity
Let F be the set of wff , S be the set of denumerable sequences
A wff F is true for the interpretation I (written |=I F) if and
only if every sequence in S satisfies F.
F is said to be false for the interpretation I if and only if no
sequence in S satisfies F.
An interpretation I is said to be a model for a set F of wff if
and only if every wff is true for I.
A wff F is valid (written |= F) if and only if F is true for all
interpretation I, over all domains.
43 / 109 SG Models and Formalisms

50. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
44 / 109 SG Models and Formalisms

51. Axiomatic Theory
An axiomatic theory is composed of:
A language and wff
A set of axioms
Inference rules
45 / 109 SG Models and Formalisms

52. Axioms
Let P, Q, R be wff and x be a variable
A1 : (P → (Q → P))
A2 : (P → (Q → R)) → ((P → Q) → (P → R)))
A3 : (¬P → ¬Q) → ((¬P → Q) → P))
A4 : ∀xP(x) → P(x)
A5 : ∀x(P → Q) → (P → ∀xQ)
where P contains no free occurrence of x.
46 / 109 SG Models and Formalisms

53. Inference Rules
Two rules
Modus Ponens
P, (P → Q) Q
- from hypothesis P and (P → Q), Q is deduced
Generalization Rule
P(x) ∀P(x)
- from hypothesis P(x), ∀P(x) is deduced
47 / 109 SG Models and Formalisms

54. Theorems
Some theorems
The law of noncontradiction: ¬(P ∧ ¬P)
Or ((P ∧ ¬P) → Q)
The law excluded middle: (P ∨ ¬P)
(¬∀xP(x) → ∃x¬P(x))
(¬∃xP(x) → ∀x¬P(x))
48 / 109 SG Models and Formalisms

55. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
49 / 109 SG Models and Formalisms

56. Predicate Calculus Properties
Completeness Theorem
Every Valid formula of the predicate calculus is a theorem.
- if |= F then F
Soundness Theorem
Every theorem of the predicate calculus is a Valid formula
- if F then |= F
50 / 109 SG Models and Formalisms

57. Predicate Calculus Properties
Decidability : the Predicate Calculus is undecidable
There is no decision procedure to determine whether arbitrary
formulas are theorems (Church, Turing, Post, Markov).
Nevertheless, if a formula F is valid, there is a constructive proof
that F is valid.
- From the soundness theorem, we can conclude that F is a theorem.
- The predicate calculus is semidecidable.
51 / 109 SG Models and Formalisms

58. Predicate Calculus Properties
Axiomatic and model theory and their properties:
Model Theory
Satisfiability
Truth
Validity
Axiomatic Theory
Axioms
Inference rules
Deduction
Theorems
≡ |=
Completeness
Soundness
52 / 109 SG Models and Formalisms

59. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
53 / 109 SG Models and Formalisms

60. Resolution Principles
For predicate calculus, the resolution is as follows:
Conjunctive normal forms are used
It is a refutation demonstrating that a set of clauses is
unsatisfiable
Conjunctive normal forms : 3 stages are necessary to deal with
quantifiers and variables
1. Prenex normal forms
A formula F is in Prenex Normal Form if and only if the formula
is in the form of (Q1x1)(Q2x2), ..., (Qnxn)(M) where
- (Qi xi ), i = 1, ..., n, is either (∀xi ) or (∃xi )
- M is a formula containing no quantifiers
54 / 109 SG Models and Formalisms

61. Resolution Principles
2. Skolem Standard Forms
A formula F is in Skolem Normal Form iff the formula is in the
form of (∀x1)(∀x2), ..., (∀xn)(M) where M is a formula containing
no quantifier
In a Prenex Standard Form, for an existential quantifier (∃x)
having n universal quantifiers on variables (x1, x2, ..., xn) appearing
before, all occurrences of x are replaced by a n-place function
f (x1, x2, ..., xn) and (∃x) is eliminated.
If n = 0, all occurrences of x are replaced by a constant.
3. Conjonctive Normal Form: a Skolem Standard Form is rewritten
to obtain a Conjunctive Normal Form
55 / 109 SG Models and Formalisms

62. Resolution Principles
The Herbrand Universe of a set of clauses
A set F of clauses is unsatisfiable if and only if it is false under
all interpretations I over all domains
Impossible to consider all interpretations I over all domains
There is a special domain H, called the Herbrand Universe of F,
"replacing all domains"
56 / 109 SG Models and Formalisms

63. Resolution Principles
H, the Herbrand Universe of a set of clauses
1. H0 is the set of constants appearing in F. If no constant is
appearing in F, H0 is to consist to a single constant, H0 = {a}
2. Hi+1 be the union of Hi and the set of all terms of the form
f n
(t1, t2, ..., tn) for all n-place functions f n
occurring in F, where
t1, t2, ..., tn ∈ Hi
3. H∞ is the Herbrand Universe of F
4.
57 / 109 SG Models and Formalisms

64. Resolution Principles
H, the Herbrand Universe of a set of clauses
F = {P(a), ¬P(x) ∨ P(f (x))}
1. H0 = {a}
2. H1 = {a, f (a)}
3. H2 = {a, f (a), f (f (a))}
4. H3 = {a, f (a), f (f (a)), f (f (f (a)))}
5. ..
6. ...
7. H∞ = {a, f (a), f (f (a)), f (f (f (a))), .....}
58 / 109 SG Models and Formalisms

65. Resolution Principles
Herbrand’s Theorem
Definition: A ground instance of a clause C of a set of clauses F
is a clause obtained by replacing variables in C by members of the
Herbrand Universe of F.
Herbrand’s Theorem: A set F of clauses is unsatisfiable if and only
if there is a finite unsatisfiable set F of ground instances of clauses
of F.
59 / 109 SG Models and Formalisms

66. Resolution Principles
Definition: A substitution is a finite set of the form
{t1/x1, ..., tn/xn} where every ti is a term and every xi is a variable
60 / 109 SG Models and Formalisms

67. Resolution Principles
Definition: A substitution is a finite set of the form
{t1/x1, ..., tn/xn} where every ti is a term and every xi is a variable
Definition: Let θ = {t1/x1, ..., tn/xn} be a substitution et E be an
expression, Eθ is an expression obtained from E by replacing
simultaneously each occurrence of the variable xi (1 ≤ i ≤ n) by
the term ti in E. Eθ is called an instance of E.
60 / 109 SG Models and Formalisms

68. Resolution Principles
Definition: A substitution is a finite set of the form
{t1/x1, ..., tn/xn} where every ti is a term and every xi is a variable
Definition: Let θ = {t1/x1, ..., tn/xn} be a substitution et E be an
expression, Eθ is an expression obtained from E by replacing
simultaneously each occurrence of the variable xi (1 ≤ i ≤ n) by
the term ti in E. Eθ is called an instance of E.
The instance definition is compatible with that of ground instance
of a clause.
60 / 109 SG Models and Formalisms

69. Resolution Principles
A Substitution
{f (y)/y, a/z, f (g(b))/x}
An instance
θ = {a/x, f (b)/y, b/z},
E = Q(x, y) ∨ P(y, z)
Then, Eθ = Q(a, f (b)) ∨ P(f (b), b)
61 / 109 SG Models and Formalisms

70. Resolution Principles
Definition: Composition of substitutions
Let θ = {t1/x1, ..., tn/xn} and λ = {u1/y1, ..., um/ym} be two
substitutions;
then, the substitution composed of θ et λ, denoted by θ ◦ λ, that is
obtained from the set {t1λ/x1, ..., tnλ/xn, u1/y1, ..., um/ym}
by deleting any element ti λ/xi for which ti λ = xi and any element
uj/yj such that yj is among{x1, x2, ..., xn}
62 / 109 SG Models and Formalisms

71. Resolution Principles
Composition of Substitutions
θ = {t1/x1, t2/x2} = {f (y)/x, z/y}
λ = {u1/y1, u2/y2, u3/y3} = {a/x, b/y, y/z}
{t1λ/x1, ..., tnλ/xn, u1/y1, ..., um/ym} =
{f (b)/x, y/y, a/x, b/y, y/z}
After deletions: θ ◦ λ = {f (b)/x, y/z}
Comments: θ ◦ (λ ◦ β) = (θ ◦ λ) ◦ β; ◦ β = β ◦ with the
empty substitution.
63 / 109 SG Models and Formalisms

72. Resolution Principles
Definition: Unifier
A substitution θ is called a unifier for a set {E1, E2, ..., Ek} if
and only if E1θ = E2θ = ... = Ekθ. The set {E1, E2, ..., Ek} is
said to be unifiable if there is a unifier for it.
Several unifiers may be exist for a set F of formulae
Definition: Most General Unifier
A unifier σ for a set {E1, E2, ..., Ek} of formulae is a Most
General Unifier if and only if each unifier θ there is a
substitution λ such that θ = σ ◦ λ
64 / 109 SG Models and Formalisms

73. Resolution Principles
Let P(g(y)) et P(x) be formulae, σ, λ, θ can be defined as follows:
θ = {g(a)/x}, λ = {a/y}, σ = {g(y)/x}
σ is the most general substitution
Most General Unifier
Let U be the set of unifiers, F be a set of formulae and S be the
set of substitutions on F.
∀α ∈ U, ∃β ∈ S such that α = β ◦ σ
The most general unifier (when it exists), denoted MGU (Most
General Unifier) is the most general substitution that match
formulae and it is unique.
65 / 109 SG Models and Formalisms

74. Resolution Principles
The resolution principle is composed of two inference rules: the
resolution rule and the reduction rule
Resolution Rule: the formula C is the resolvent of the two clauses
A and B if and only if
A = P ∨ D
B = P1 ∨ E
C = (Dθ ∨ E)σ
θ is a renaming substitution so that Dθ and E are formulae with
disjoint variables. σ is the most general unifier of P et P1 such
that P et P1 are complementary literals (or complementary pairs)
66 / 109 SG Models and Formalisms

75. Resolution Principles
The resolution rule can be rewrite as follows:
P ∨ D, P1 ∨ E (Dθ ∨ E)σ
Example
Let A = P(x, c) ∨ R(x) and B = ¬P(c, c) ∨ Q(x)
Let D = R(x) and E = Q(x)
C = R(c) ∨ Q(x) with θ = {y/x} in A and σ = {c/y}
67 / 109 SG Models and Formalisms

76. Resolution Principles
Reduction rule
Let A = P ∨ P1 ∨ B be a clause, C is the resolvent of A if and only
if:
Pσ = P1σ, σ Most General Unifier of P et P1
C = Pσ ∨ Bσ
The rule may be rewrite as follows:
P ∨ P1 ∨ B Pσ ∨ Bσ with Pσ = P1σ
Example
Let A = P(x, g(y)) ∨ P(f (c), z) ∨ R(x, y, z)
C = R(f (c), y, g(y)) ∨ P(f (c), g(y)) with
σ = {f (c)/x, g(y)/z}
68 / 109 SG Models and Formalisms

77. Resolution Principles
Theorem: a set F of clauses is unsatisfiable if and only if there is a
deduction of the empty clause from F.
Properties: the resolution principle is sound and complete, that is
to say:
If F is satisfiable, the empty clause cannot be deduced
vide.
If F is unsatisfiable, the empty clause is deduced
69 / 109 SG Models and Formalisms

78. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
70 / 109 SG Models and Formalisms

79. Resolution Strategy
The two main methods are: the management of a set of clauses
and the exploration of deduction tree.
We focus on the later. Two possible choices are available for this
strategy:
Selection of a sub-tree of the deduction tree, limitation of the
possible deductions
Selection of an exploration strategy of a sub-tree (Depth- first
search, Breadth-first search, ...)
71 / 109 SG Models and Formalisms

80. Resolution Strategy
Linear Strategy
Definition: Let S be a set of clauses and C0 a clause in S, a linear
deduction of Cn from S with C0 as initial clause has the following
properties: Ci+1 is the resolvent of Ci and Bi (resolution rule) with
Bi ∈ S or Bi = Cj such that 1 ≤ i ≤ n − 1, j < i.
72 / 109 SG Models and Formalisms

81. Resolution Strategy
Linear deduction properties (cf. Chang and Lee or Loveland):
If there is a deduction of the empty clause for S, then there is a
linear deduction of the empty clause for S.
Moreover, if S = S ∪ {C0} with S satisfiable and S unsatisfiable
then there is a linear deduction from S having C0 as initial clause.
Breadth-first exploration strategy: the linear deduction is sound
and complete.
Depth-first exploration strategy: the linear deduction is sound,
but not complete.
73 / 109 SG Models and Formalisms

82. Resolution Strategy
Input Strategy
Definition: Let S be a set of clauses and C0 be a clause in S, an
Input deduction of Cn from S with C0 as initial clause has the
following properties: Ci+1 is a resolvent obtained by the application
of the rule resolution and Bi with Bi ∈ S such that 1 ≤ i ≤ n − 1.
Even, with a Breadth-first exploration strategy, an Input
deduction is not complete.
The Input deduction tree does not contain the empty clause. but
the tree of all deductions contain the empty clause.
74 / 109 SG Models and Formalisms

83. Resolution Strategy
Input Strategy
Nevertheless, there is an interesting result in a particular case::
If S = S ∪ {C0} is unsatisfiable, C0 is a negative clause that
only contains negative literals and S only contains clauses with
exactly one positive literal (Horn clauses) then there is an input
deduction with C0 as initial clause which gives the empty clause
clause and does not use the reduction rule.
75 / 109 SG Models and Formalisms

84. Resolution Strategy
Ordered Strategy
Definition: An ordered resolution between two ordered clauses
(without common variables) C1 and C2 deduces the ordered clause
C with the following conditions:
C1 = L1 ∨ L2 ∨ ... ∨ Ln
C2 = ¬L1 ∨ L2 ∨ ... ∨ Lm
C = (L2 ∨ ... ∨ Ln ∨ L2 ∨ ... ∨ Lm)θ avec θ Most General Unifier
of L1 and ¬L1
The clause C is ordered: the clause containing the positive literal is
located at the beginning of the resolvent and the respective orders
of the two clauses are kept
76 / 109 SG Models and Formalisms

85. Resolution Strategy
Definition: Let S be a set of clauses and C0 be a clause in S, a
linear ordered deduction of Cn from S with C0 as initial clause is a
deduction obtained by applying n ordered resolutions.
Linear ordered Strategy
Definition: Let S be a set of clauses and C0 be a clause in S, an
ordered deduction of Cn from S with C0 as initial clause has the
following properties: Ci+1 is an ordered resolvent of ordered clauses
Ci and Bi (ordered resolution) with Bi ∈ S or Bi = Cj such that
1 ≤ i ≤ n1, j < i.
77 / 109 SG Models and Formalisms

86. Resolution Strategy
A linear ordered refutation is a linear ordered deduction of the
empty clause.
With a Breadth-first exploration strategy, the linear ordered
deduction is sound and complete.
The most important result is as follows:
If S = S ∪ {C0} is unsatisfiable, C0 is a negative literal and S
does not have clauses with exactly one positive literal (Horn
clauses) then there is an input and linear ordered with the initial
clause C0 leading to the empty clause.
78 / 109 SG Models and Formalisms

87. Resolution Strategy
SLD Resolution
A SLD resolution is a linear resolution with a selection function on
a set of Horn clauses.
Definition: a SLD refutation of P ∪ {¬G} is a finite SLD deduction
of P ∪ {¬G} of the empty clause via a selection function.
79 / 109 SG Models and Formalisms

88. Resolution Strategy
SLD Resolution
Definition of Derivation: Let Gi be a goal such that
A1, ..., Am, ...Ak → Gi , the clause Ci+1 such that B1, ..., Bq → A
and a selection function R. The derivation of the goal Gi+1 is
obtained from Gi with Ci+1 by using the MGU θi+1 via R if the
following conditions are filled:
Am is an atom selected by a selection function
Amθi+1 = Aθi+1 tel que θi+1 is the MGU of A et Am
Gi+1 = (A1, ..., Am−1, B1, ..., Bq, Am+1, ..., Ak)θi+1
Gi+1 is the resolvent of Gi et Ci+1. Ci+1 is a variant of A that is
to say a clause such that all variables of A has been renamed.
80 / 109 SG Models and Formalisms

89. Resolution Strategy
SLD Resolution
Definition: a SLD derivation of P ∪ {¬G} is composed of a finitite
or infinite serie G0, G1, G2, ... of goals, a serie C0, C1, C2, ... of
clauses’ variants of the program P and a serie θ1, θ2, ... of MGU
such that Gi+1 is derived of Gi and Ci+1 and uses θi+1 via R.
A selection function is an application of a set of goals to a set of
atoms, such that the function value for a goal is alsways an atom.
The later is called the selected atom.
Independence of the function selection: if P ∪ {¬G} is
unsatisfiable then there is always a SLD refutation that will use
this function selection. The space search traversed by a SLD
refutation is called a SLD tree.
81 / 109 SG Models and Formalisms

90. Resolution Strategy
SLD Resolution
Let P be a program, G be a goal and R a selection fucntion, the
SLD tree for P ∪ {¬G} via R is defined as follows:
Each tree node is a goal (possibly empty)
The root is G
Let A1, A2, ..., Ak → Gi , (k ≥ 1) be a tree node and Am be the
selected atom via R, this node is a descendant for each clause
B1, ..., Bq → A such that Am et A is unifiable. the descendant is
(A1, ..., Am−1, B1, ..., Bq, Am+1, ..., Ak)θi+1 where θi+1 is the
MGU of Am and A
The empty nodes do not have descendant
82 / 109 SG Models and Formalisms

91. Resolution Strategy
SLD Resolution
The soundness of the SLD refutation rely upon the unification.
Thus, if it unifies non unifiable terms, the result will be wrong.
Occur check:
test ← P(x, x)
P(x, f (x)) ← P(x, x))
The unification algorithm has to made the occur check. Let x be a
variable that must be unified with the term t1, the ccur check aim
at detecting the presence of x into the term t1. If one consider the
above mentioned example, for demonstrating test it is necessary to
unify P(x, x) with P(y, f (y)) - after renaming the variables. These
two terms are not unifiale because x = f (x). Without the occur
check, the algorithm will unify the two terms.
83 / 109 SG Models and Formalisms

92. Outline
1 Introduction
2 Formal Systems
3 Propositional Logic
The Axiomatic Theory
Propositional Logic Properties
Resolution Principles
4 The Predicate Calculus or First Order Logic
The Model Theory or Semantics
The Axiomatic Theory
Predicate Calculus Properties
Resolution Principles
Resolution Strategy
Prolog Modeling
84 / 109 SG Models and Formalisms

93. Prolog Modeling
Concatenation Program
Conc([X|L], L1, [X|L2]) :− Conc(L, L1, L2).
Conc([], L, L).
Conc([a,b], [c,d], L)?
85 / 109 SG Models and Formalisms

94. Prolog Modeling
Ancestor Program, Version 1
Ancestor(X,Y) :− Parents(X,Z), Ancestor(Z,Y).
Ancestor(X,Y) :− Parents(X,Y).
Parents(X,Y) :− Father(X,Y).
Parents(X,Y) :− Mother(X,Y).
Version 2
Ancestor(X,Y) :− Parents(X,Y).
Ancestor(X,Y) :− Parents(X,Z), Ancestor(Z,Y).
Version 3
Ancestor(X,Y) :− Ancestor(Z,Y), Parents(X,Z).
Ancestor(X,Y) :− Parents(X,Y).
86 / 109 SG Models and Formalisms

95. Prolog Modeling
Eight Queens’ Problem
1 2 3 4 5 6 7 8
1 X
2 X
3 X
4 X
5 X
6 ? ? ?
7 ? ? ?
8 ? ? ?
87 / 109 SG Models and Formalisms

96. Prolog Modeling
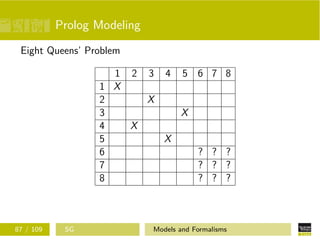
Eight Queens’ Program
Put(Listdd, Listdg ,Col,8, Result ).
Put(Listdd, Listdg ,Col,Row,Result) :−
Row_1 is Row + 1,
column(I), not(member(I,Col)),
Dd is Row_1 + I, Dg is I − Row_1,
not(member(Dd,Listdd)),
not(member(Dg,Listdg)),
Put([Dd|Listdd ],[ Dg|Listdg ],[ I |Col ], Row_1,[[Row_1,I]|Result]).
Column(1). Column(2). Column(3). Column(4).
Column(5). Column(6). Column(7). Column(8).
88 / 109 SG Models and Formalisms

97. Prolog Theorem Proving
Concatenation Program
Conc([X|L], L1, [X|L2]) :− Conc(L, L1, L2).
Conc([], L, L).
Conc([a,b], [c,d], L)?
∀X, L, L1, L2 (Conc(f (X, L), L1, f (X, L2)) ∨ ¬Conc(L, L1, L2))∧
∀L (Conc(f (empty), L, L)∧
∀L ¬Conc(f (a, f (b, f (empty))), f (c, f (d, f (empty))), L)
89 / 109 SG Models and Formalisms

98. Prolog Theorem Proving
Concatenation Demonstration
¬Conc(f (a, f (b, f (empty))), f (c, f (d, f (empty))), L )
Conc(f (X, L), L1, f (X, L2)) ∨ ¬Conc(L, L1, L2))
¬Conc(f (b, f (empty)), f (c, f (d, f (empty))), L2)
σ =
{a/X, f (b, f (empty))/L, f (c, f (d, f (empty)))/L1, f (a, L2)/L }
Resolvent : ¬Conc(f (b, f (empty)), f (c, f (d, f (empty))), L2)
90 / 109 SG Models and Formalisms

99. Prolog Theorem Proving
Concatenation Demonstration
¬Conc(f (b, f (empty)), f (c, f (d, f (empty))), L2)
Conc(f (X, L), L1, f (X, L2 )) ∨ ¬Conc(L, L1, L2 )
¬Conc(f (empty), f (c, f (d, f (empty))), L2 )
σ = {b/X, f (empty)/L, f (c, f (d, f (empty)))/L1, f (b, L2 )/L2}
Resolvent : ¬Conc(f (empty), f (c, f (d, f (empty))), L2 )
91 / 109 SG Models and Formalisms

100. Prolog Theorem Proving
Concatenation Demonstration
¬Conc(f (b, f (empty)), f (c, f (d, f (empty))), L2)
Conc(f (X, L), L1, f (X, L2 )) ∨ ¬Conc(L, L1, L2 )
¬Conc(f (empty), f (c, f (d, f (empty))), L2 )
σ = {b/X, f (empty)/L, f (c, f (d, f (empty)))/L1, f (b, L2 )/L2}
Resolvent : ¬Conc(f (empty), f (c, f (d, f (empty))), L2 )
92 / 109 SG Models and Formalisms

101. Prolog Theorem Proving
Concatenation Demonstration
¬Conc(f (empty), f (c, f (d, f (empty))), L2 ))
Conc(f (empty), L, L)
σ = {f (c, f (d, f (empty)))/L, f (c, f (d, f (empty)))/L2 }
Resolvent :
93 / 109 SG Models and Formalisms

102. Prolog Theorem Proving
Ancestor Program
Ancestor(X,Y) :− Parents(X,Z), Ancestor(Z,Y).
Ancestor(X,Y) :− Parents(X,Y).
Parents(X,Y) :− Father(X,Y).
Parents(X,Y) :− Mother(X,Y).
Father(a,b). Father(b,c). Father(d,f ). Father(e,g).
Mother(a,d). Mother(d,e). Mother(a,h). Mother(b,i).
Ancesotr(X,Y) ?
94 / 109 SG Models and Formalisms

103. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
95 / 109 SG Models and Formalisms

104. Prolog Theorem Proving
Ancestor Demonstration
¬Ancestor(T, U)
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )
¬Parents(T, Z) ∨ ¬Ancestor(Z, U)
σ = {T/X, U/Y }
Resolvent : ¬Parents(T, Z) ∨ ¬Ancestor(Z, U)
96 / 109 SG Models and Formalisms

105. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
97 / 109 SG Models and Formalisms

106. Prolog Theorem Proving
Ancestor Demonstration
¬Parents(T, Z) ∨ ¬Ancestor(Z, U)
(Parents(X, Y ) ∨ ¬Father(X, Y )
¬Father(T, Z) ∨ ¬Ancestor(Z, U)
σ = {T/X, Z/Y }
Resolvent : ¬Father(T, Z) ∨ ¬Ancestor(Z, U)
98 / 109 SG Models and Formalisms

107. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
99 / 109 SG Models and Formalisms

108. Prolog Theorem Proving
Ancestor Demonstration
¬Father(T, Z) ∨ ¬Ancestor(Z, U)
Father(a, b)
¬Ancestor(b, U)
σ = {a/T, b/Z}
Resolvent : ¬Ancestor(b, U)
100 / 109 SG Models and Formalisms

109. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
101 / 109 SG Models and Formalisms

110. Prolog Theorem Proving
Ancestor Demonstration
¬Ancestor(b, U)
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )
¬Parents(b, Z) ∨ ¬Ancestor(Z, U)
σ = {b/Y , U/Y }
Resolvent : ¬Parents(b, Z) ∨ ¬Ancestor(Z, U)
102 / 109 SG Models and Formalisms

111. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
103 / 109 SG Models and Formalisms

112. Prolog Theorem Proving
Ancestor Demonstration
¬Parents(b, Z) ∨ ¬Ancestor(Z, U)
(Parents(X, Y ) ∨ ¬Father(X, Y )
¬Father(b, Z) ∨ ¬Ancestor(Z, U)
σ = {b/X, U/Y }
Resolvent : ¬Father(b, Z) ∨ ¬Ancestor(Z, U)
104 / 109 SG Models and Formalisms

113. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
105 / 109 SG Models and Formalisms

114. Prolog Theorem Proving
Ancestor Demonstration
¬Father(b, Z) ∨ ¬Ancestor(Z, U)
Father(b, c)
¬Ancestor(c, U)
σ = {c/Z}
Resolvent : ¬Ancestor(c, U)
106 / 109 SG Models and Formalisms

115. Prolog Theorem Proving
Ancestor Program
∀X, Y , Z
(Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )∧
∀X, Y (Ancestor(X, Y ) ∨ ¬Parents(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Father(X, Y )∧
∀X, Y (Parents(X, Y ) ∨ ¬Mother(X, Y )∧
Father(a, b) ∧ Father(b, c) ∧ Father(d, f ) ∧ Father(e, g)∧
Mother(a, d) ∧ Mother(d, e) ∧ Mother(a, h) ∧ Mother(b, i)∧
¬Ancestor(X, Y )
107 / 109 SG Models and Formalisms

116. Prolog Theorem Proving
Ancestor Demonstration
¬Ancestor(c, U)
Ancestor(X, Y ) ∨ ¬Parents(X, Z) ∨ ¬Ancestor(Z, Y )
¬Parents(c, Z) ∨ ¬Ancestor(Z, U)
σ = {c/X, U/Y }
Resolvent : ¬Parents(c, Z) ∨ ¬Ancestor(Z, U)
108 / 109 SG Models and Formalisms

117. Prolog Theorem Proving
Ancestor Demonstration
¬Parents(c, Z) ∨ ¬Ancestor(Z, U)
Parents(X, Z ) ∨ ¬Father(Z , Y )
¬Father(c, U) ∨ ¬Ancestor(Z , U )
σ = {c/X, Z/Z }
Resolvent : ¬Father(c, U ) ∨ ¬Ancestor(Z , U )
109 / 109 SG Models and Formalisms