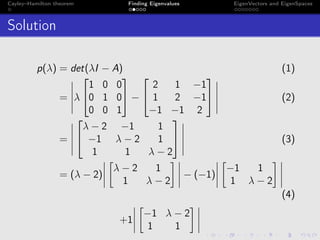
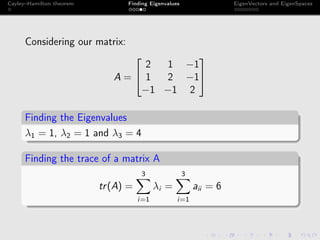
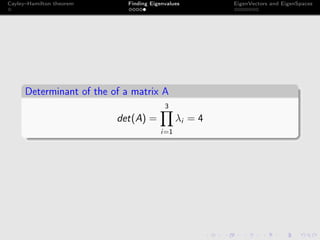
The document discusses the Cayley-Hamilton theorem, which states that every square matrix satisfies its own characteristic equation. It provides a detailed example of finding the eigenvalues, eigenvectors, and eigenspaces for a specific matrix using this theorem. The findings include characteristic equations, traces, and determinants associated with the given matrix.

1. Cayley–Hamilton theorem - Eigenvalues,
Eigenvectors and Eigenspaces
Isaac Amornortey Yowetu
NIMS-GHANA
March 17, 2021

2. Cayley–Hamilton theorem Finding Eigenvalues EigenVectors and EigenSpaces
Content
1 Cayley–Hamilton theorem
2 Finding Eigenvalues
3 EigenVectors and EigenSpaces

3. Cayley–Hamilton theorem Finding Eigenvalues EigenVectors and EigenSpaces
Cayley–Hamilton theorem
Every square matrix satisfies its own characteristic equation.
Thus:
p(λ) = det(λI − A)
Substituting the matrix A for λ in the polynomial,
p(λ) = det(λI − A) results in a zero matrix.
Thus:
p(A) = 0

4. Cayley–Hamilton theorem Finding Eigenvalues EigenVectors and EigenSpaces
Example : Using Non-singular Matrix
Consider the given matrix:
A =


2 1 −1
1 2 −1
− −1 2


Find the characteristic equation of the square matrix and
hence find the eigenvalues, eigenvectors and eigenspaces.

5. Cayley–Hamilton theorem Finding Eigenvalues EigenVectors and EigenSpaces
Solution
p(λ) = det(λI − A) (1)
=

10. λ


1 0 0
0 1 0
0 0 1

 −


2 1 −1
1 2 −1
−1 −1 2



15. (2)
=