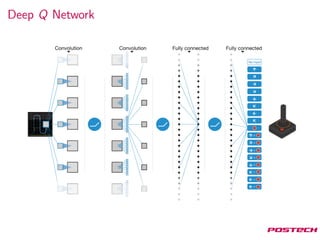
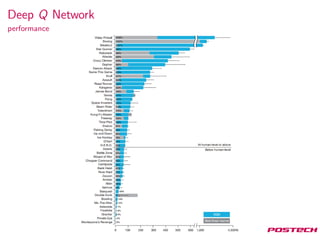
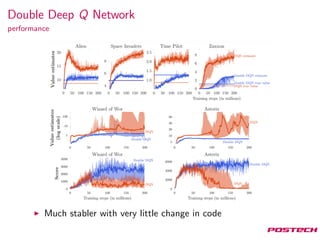
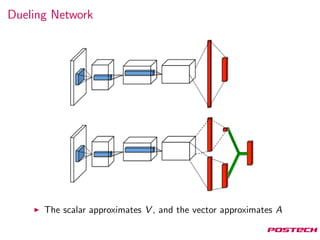
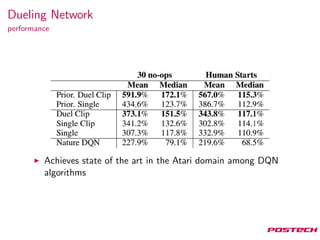
This document summarizes reinforcement learning algorithms like Deep Q-Network (DQN), Double DQN, prioritized experience replay, and the Dueling Network architecture. DQN uses a deep neural network to estimate the Q-function and select actions greedily during training. Double DQN decouples action selection from evaluation to reduce overestimation. Prioritized replay improves sampling to focus on surprising transitions. The Dueling Network separately estimates the state value and state-dependent action advantages to better determine the optimal action. It achieves state-of-the-art performance on Atari games by implicitly splitting credit assignment between choosing now versus later actions.

1. Dueling Network Architectures for Deep
Reinforcement Learning (ICML 2016)
Yoonho Lee
Department of Computer Science and Engineering
Pohang University of Science and Technology
October 11, 2016

2. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

3. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

4. Definition of RL
general setting of RL

5. Definition of RL
atari setting

6. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

7. Mathematical formulations
objective of RL
Definition
Return Gt is the cumulative discounted reward from time t
Gt = rt+1 + γrt+2 + γ2
rt+3 + . . .

8. Mathematical formulations
objective of RL
Definition
Return Gt is the cumulative discounted reward from time t
Gt = rt+1 + γrt+2 + γ2
rt+3 + . . .
Definition
A policy π is a function that selects actions given states
π(s) = a
The goal of RL is to find π that maximizes G0

9. Mathematical formulations
Q-Value
Gt =
∞
i=0
γk
rt+i+1
Definition
The action-value (Q-value) function Qπ(s, a) is the expectation of
Gt under taking action a, and then following policy π afterwards
Qπ(s, a) = Eπ[Gt|St = s, At = a, At+i = π(St+i )∀i ∈ N]
”How good is action a in state s?”

10. Mathematical formulations
Optimal Q-value
Definition
The optimal Q-value function Q∗(s, a) is the maximum Q-value
over all policies
Q∗(s, a) = max
π
Qπ(s, a)

11. Mathematical formulations
Optimal Q-value
Definition
The optimal Q-value function Q∗(s, a) is the maximum Q-value
over all policies
Q∗(s, a) = max
π
Qπ(s, a)
Theorem
There exists a policy π∗ such that Qπ∗ (s, a) = Q∗(s, a) for all s, a
Thus, it suffices to find Q∗

12. Mathematical formulations
Q-Learning
Bellman Optimality Equation
Q∗(s, a) satisfies the following equation:
Q∗(s, a) = R(s, a) + γ
s
P(s |s, a)max
a
Q∗(s , a )

13. Mathematical formulations
Q-Learning
Bellman Optimality Equation
Q∗(s, a) satisfies the following equation:
Q∗(s, a) = R(s, a) + γ
s
P(s |s, a)max
a
Q∗(s , a )
Q-Learning
Let a be -greedy w.r.t. Q, and a be optimal w.r.t. Q. Q
converges to Q∗ if we iteratively apply the following update:
Q(s, a) ← α(R(s, a) + γQ(s , a )) + (1 − α)Q(s, a)

14. Mathematical formulations
Other approcahes to RL
Value-Based RL
Estimate Q∗(s, a)
Deep Q Network
Policy-Based RL
Search directly for optimal policy π∗
DDPG, TRPO. . .
Model-Based RL
Use the (learned or given) transition model of environment
Tree Search, DYNA . . .

15. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

16. Neural Fitted Q Iteration
Supervised learning on (s,a,r,s’)

17. Neural Fitted Q Iteration
input

18. Neural Fitted Q Iteration
target equation

19. Neural Fitted Q Iteration
Shortcomings
Exploration is independent of experience
Exploitation does not occur at all
Policy evaluation does not occur at all
Even in exact(table lookup) case, not guaranteed to converge
to Q∗

20. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

21. Deep Q Network
action policy
Choose an -greedy policy w.r.t. Q

22. Deep Q Network
network freezing
Get a copy of the network every C steps for stability

23. Deep Q Network

24. Deep Q Network

25. Deep Q Network
performance

26. Deep Q Network
overoptimism
What happens when we overestimate Q?

27. Deep Q Network
Problems
Overestimation of the Q function at any s spills over to
actions that lead to s → Double DQN
Sampling transitions uniformly from D is inefficient →
Prioritized Experience Replay

28. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

29. Double Deep Q Network
target
We can write the DQN target as:
Y DQN
t = Rt+1 + γQ(St+1, argmax
a
Q(St+1, a; θ−
t ); θ−
t )
Double DQN’s target is:
Y DDQN
t = Rt+1 + γQ(St+1, argmax
a
Q(St+1, a; θt); θ−
t )
This has the effect of decoupling action selection and action
evaluation

30. Double Deep Q Network
performance
Much stabler with very little change in code

31. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

32. Prioritized Experience Replay
Update ’more surprising’ experiences more frequently

33. Outline
Reinforcement Learning
Definition of RL
Mathematical formulations
Algorithms
Neural Fitted Q Iteration
Deep Q Network
Double Deep Q Network
Prioritized Experience Replay
Dueling Network

34. Dueling Network
The scalar approximates V , and the vector approximates A

35. Dueling Network
forward pass equation
The exact forward pass equation is:
Q(s, a; θ, α, β) = V (s; θ, β) + (A(s, a; θ, α) − max
a
A(s, a ; θ, α))
The following module was found to be more stable without losing
much performance:
Q(s, a; θ, α, β) = V (s; θ, β) + (A(s, a; θ, α) −
1
|A|
a
A(s, a ; θ, α))

36. Dueling Network
attention
Advantage network only pays attention when current action
crucial

37. Dueling Network
performance
Achieves state of the art in the Atari domain among DQN
algorithms

38. Dueling Network
Summary
Since this is an improvement only in network architecture,
methods that improve DQN(e.g. Double DQN) are all
applicable here as well
Solves problem of V and A typically being of different scale
Updates Q values more frequently than a single-stream DQN,
where only a single Q value is updated for each observation
Implicitly splits the credit assignment problem into a recursive
binary problem of “now or later”

39. Dueling Network
Shortcomings
Only works for |A| < ∞
Still not able to solve tasks involving long-term planning
Better than DQN, but sample complexity is still high
-greedy exploration is essentially random guessing