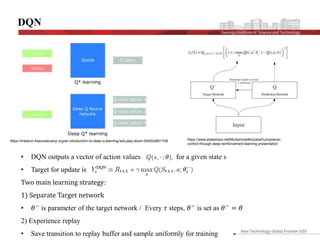
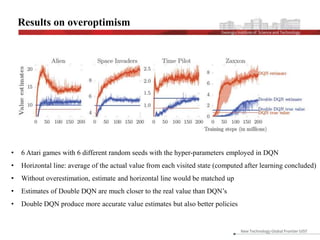
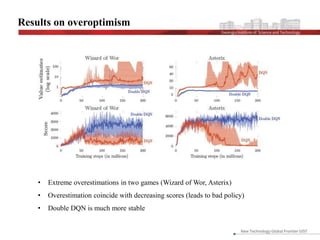
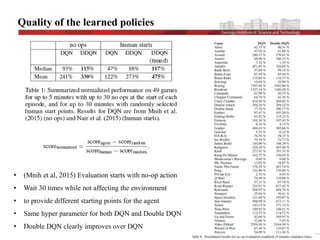
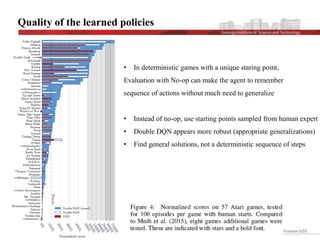
This document discusses the implementation and advantages of deep reinforcement learning using Double Q-Learning, as a solution to the overestimation problems faced by traditional Q-Learning and DQN in Atari games. It introduces the Double DQN algorithm, which reduces overestimation by decoupling action selection and evaluation within the framework of Q-learning, leading to improved performance and more accurate value estimates. The findings demonstrate that Double DQN produces more stable training outcomes and better overall policies compared to its predecessors, particularly in complex environments.

1. Lab Seminar
Deep Reinforcement Learning
with Double Q-Learning
Seunghyeok Back
2018. 11. 05
Graduate Student in MS&ph.D integrated course
Artificial intelligence Lab
shback@gist.ac.kr
School of Integrated Technology (SIT)
Gwangju Institute of Science and Technology (GIST)

2. Introduction
(2016) Deep Reinforcement Learning with Double Q-Learning
Van Hasselt, Hado, Arthur Guez, and David Silver (Deepmind), AAAI
Double Q-learning + DQN = > Double DQN
• DQN suffers from substantial overestimations in some of Atari game
• Generalize Double Q-learning (tabular setting -> large-scale function approximation)
• Propose Double DQN algorithm (reduce overestimation and leads to much better performance)

3. RL goal: Find optimal policy
Q-learning: Find optimal policy using action-value function
Update of Q-function
Too large problems to learn all action values in all states -> Function approximation
1) Parameterize Q function
2) Update Q function toward to Target value (similar as SGD)
Target value (Bellman equation)
Overestimation in Q-learning
Target value – current predicted Q-value
= Temporal Difference (TD) Error
Learning rate
Gradient of current predicted Q-value

4. • Sometimes learn unrealistically high action value due to maximization step
• Tends to prefer overestimated to underestimated values
• Overestimation is attributed to
1) insufficiently flexible function approximation 2) noise 3) estimation errors
Question: Do the overestimations negatively affects performance?
 Yes, if the overestimations are not uniform & not concentrated at states about which we wish to learn
 DQN : sufficiently flexible function approximation (deep), no harmful effects of noise (deterministic)
 Favorable setting, but overestimation occurs!
 Double DQN reduce overestimation and leads to better results on Atari domain
Overestimation in Q-learning

5. • DQN outputs a vector of action values for a given state s
• Target for update is
Two main learning strategy:
1) Separate Target network
• 𝜃−
is parameter of the target network / Every 𝜏 steps, 𝜃−
is set as 𝜃−
= 𝜃
2) Experience replay
• Save transition to replay buffer and sample uniformly for training
DQN
https://medium.freecodecamp.org/an-introduction-to-deep-q-learning-lets-play-doom-54d02d8017d8 https://www.slideshare.net/MuhammedKocaba/humanlevel-
control-through-deep-reinforcement-learning-presentation

6. • (Q-learning, DQN) Use same value Q both to select and to evaluate an action -> Overestimation
• (Double Q-learning) One for selection of an action, one for evaluation of an action
• Two value functions, each of weights are 𝜃 and 𝜃′
• Update one of the two value functions, randomly
• Select action with Q(𝑆, 𝑎; 𝜃), evaluate this action with Q(𝑆, 𝑎; 𝜃′
)
• Decouple the selection from the evaluation
Double Q-learning
Selection (inner Q) Evaluation (outer Q)

7. Use target network as a second value function without introducing additional networks
Double Q-learning
• Pick one from two value function and update
• Each value function can be used for both evaluation and selection
Double DQN
• Target network Q(𝑆, 𝑎; 𝜃−
) is used only for the evaluation, not for the selection
• Remains a periodic copy of the online network to the target network
• Value functions are not fully decoupled from each other
• Minimal possible change of DQN towards Double Q-learning
• Get most of the benefit of Double Q-learning, while keeping the rest of the DQN
• Fair comparison and minimal computational overhead
Double DQN

8. • Testbed: Atari 2600 games
• High-dimensional inputs / the visual and mechanic of games are vary substantially b/w games
• Same experimental setup and network architecture with DQN (Mnih et al, 2015)
• Single GPU for 200M frames per each game
Experiment
https://ocr.space/blog/2015/02/playing-atari-deep-reinforcement-learning.html

9. Results on overoptimism
• 6 Atari games with 6 different random seeds with the hyper-parameters employed in DQN
• Horizontal line: average of the actual value from each visited state (computed after learning concluded)
• Without overestimation, estimate and horizontal line would be matched up
• Estimates of Double DQN are much closer to the real value than DQN’s
• Double DQN produce more accurate value estimates but also better policies

10. Results on overoptimism
• Extreme overestimations in two games (Wizard of Wor, Asterix)
• Overestimation coincide with decreasing scores (leads to bad policy)
• Double DQN is much more stable

11. Quality of the learned policies
• (Mnih et al, 2015) Evaluation starts with no-op action
• Wait 30 times while not affecting the environment
• to provide different starting points for the agent
• Same hyper parameter for both DQN and Double DQN
• Double DQN clearly improves over DQN

12. Quality of the learned policies
• In deterministic games with a unique staring point,
Evaluation with No-op can make the agent to remember
sequence of actions without much need to generalize
• Instead of no-op, use starting points sampled from human expert
• Double DQN appears more robust (appropriate generalizations)
• Find general solutions, not a deterministic sequence of steps