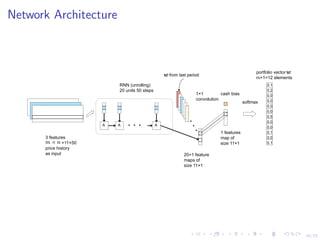
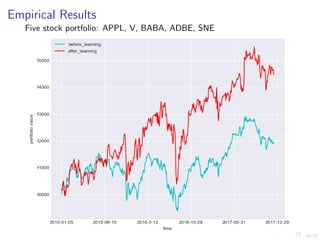
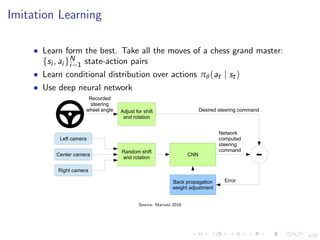
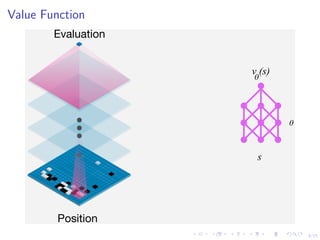
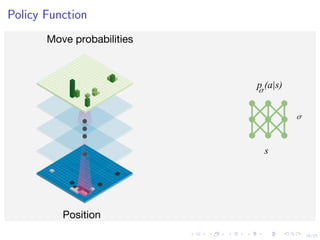
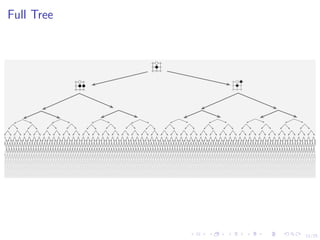
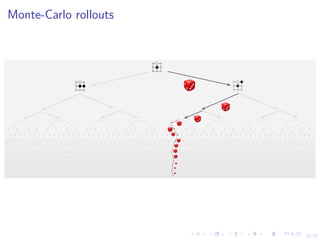
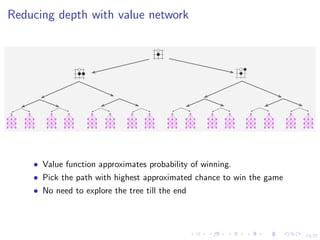
This document discusses using deep reinforcement learning and deep learning techniques for agent-based models. It discusses using deep learning to approximate policy and value functions, using imitation learning to learn from expert demonstrations, and using Q-learning and model-based reinforcement learning to optimize agent behavior. Micro-emulations use deep learning to model individual agent behavior, while macro-emulations aim to emulate the overall system behavior. Open problems include using reinforcement learning to find optimal policies given an agent-based model simulator.







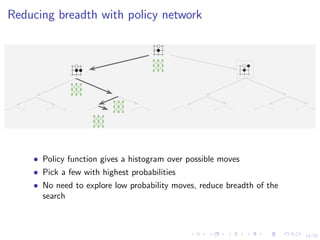


.](https://image.slidesharecdn.com/6-polsonsokolovbayes-rl-190808164925/85/GDRR-Opening-Workshop-Deep-Reinforcement-Learning-for-Asset-Based-Modeling-Nick-Polson-August-7-2019-17-320.jpg)