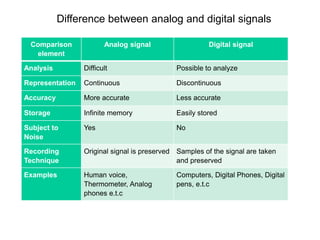
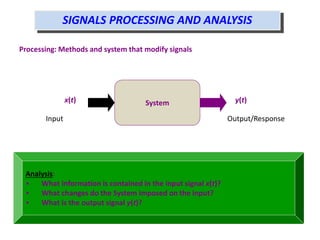
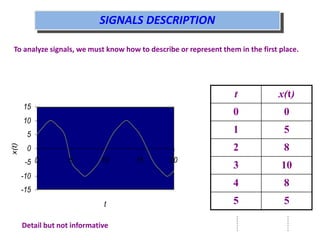
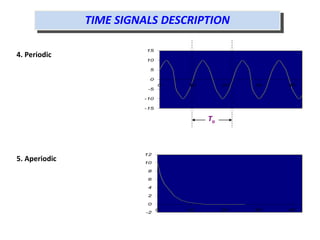
A signal can be defined as a pattern of variation that carries information over time. Signals can be continuous analog signals defined by mathematical functions, or discrete digital signals represented by discrete samples. Analog signals are more accurate but digital signals are easier to store and analyze. Conversion between analog and digital signals involves sampling the analog signal at discrete time intervals and quantizing the amplitude into discrete levels. Signals can be analyzed in the time domain, looking at amplitude variation over time, or the frequency domain, looking at how many times different events occur over the total observation period.

1. Signals
&
Systems

2. 2/20
What is a Signal?
• A signal is a pattern of variation of some form
• Signals are variables that carry information
Examples of signal include:
Electrical signals
– Voltages and currents in a circuit
Acoustic signals
– Acoustic pressure (sound) over time
Mechanical signals
– Velocity of a car over time
Video signals
– Intensity level of a pixel (camera, video) over time

3. SIGNALS
Information expressed in different forms
Stock Price
Transmit
Waveform
$1.00, $1.20, $1.30, $1.30, …
Data File
x(t)
00001010 00001100 00001101
Primary interest of Electronic Engineers

4. How is a Signal Represented?
Mathematically, signals are represented as a function of
one or more independent variables.
Here we shall be concerned with signals that are a
function of a single variable: time
t
f(t)

5. What is a System?
• Systems process input signals to produce output
signals
Examples:
– A circuit involving a capacitor can be viewed as a
system that transforms the source voltage (signal) to
the voltage (signal) across the capacitor
– A CD player takes the signal on the CD and transforms
it into a signal sent to the loud speaker
– A communication system is generally composed of
three sub-systems, the transmitter, the channel and the
receiver. The channel typically attenuates and adds
noise to the transmitted signal which must be
processed by the receiver

6. SIGNALS PROCESSING AND ANALYSIS
Processing: Methods and system that modify signals
System y(t)
x(t)
Analysis:
• What information is contained in the input signal x(t)?
• What changes do the System imposed on the input?
• What is the output signal y(t)?
Input Output/Response

7. SIGNALS DESCRIPTION
To analyze signals, we must know how to describe or represent them in the first place.
-15
-10
-5
0
5
10
15
0 5 10 15 20
t
x(t)
t x(t)
0 0
1 5
2 8
3 10
4 8
5 5
Detail but not informative

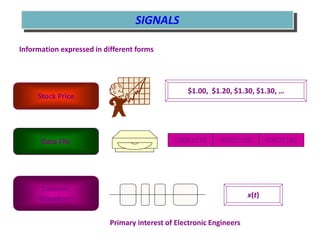
8. TIME SIGNALS DESCRIPTION
1. Mathematical expression: x(t)=Asin()
2. Continuous (Analogue)
-15
-10
-5
0
5
10
15
0 5 10 15 20
3. Discrete (Digital)
x[n]
n

9. TIME SIGNALS DESCRIPTION
4. Periodic
-15
-10
-5
0
5
10
15
0 10 20 30 40
To
5. Aperiodic
-2
0
2
4
6
8
10
12
0 10 20 30 40

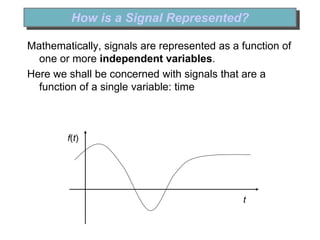
10. Continuous & Discrete-Time Signals
Continuous-Time Signals
Most signals in the real world are
continuous time, as the scale is
infinitesimally fine.
Eg voltage, velocity,
Denote by x(t), where the time
interval may be bounded (finite) or
infinite
Discrete-Time Signals
Some real world and many digital
signals are discrete time, as they
are sampled
E.g. pixels, daily stock price (anything
that a digital computer processes)
Denote by x[n], where n is an integer
value that varies discretely
x(t)
t
x[n]
n

11. Analog signals
• A signal could be an analog quantity that means it is
defined with respect to the time. It is a continuous
signal.
• These signals are defined over continuous
independent variables. They are difficult to analyze,
as they carry a huge number of values.
• They are very much accurate due to a large sample
of values. In order to store these signals , you require
an infinite memory because it can achieve infinite
values on a real line.
• Analog signals are denoted by sin waves.

12. Analog signals
Human voice
Human voice is an example of analog signals. When
you speak, the voice that is produced travel through
air in the form of pressure waves and thus belongs to
a mathematical function, having independent
variables time.

13. Digital signals
• As compared to analog signals, digital signals are very
easy to analyze. They are discontinuous signals.
• The word digital stands for discrete values and hence it
means that they use specific values to represent any
information.
• In digital signal, only two values are used to represent
something i-e: 1 and 0 (binary values).
• Digital signals are less accurate then analog signals
because they are the discrete samples of an analog
signal taken over some period of time.
• However digital signals are not subject to noise. So
they last long and are easy to interpret.

14. Digital signals
Computer keyboard
Whenever a key is pressed from the keyboard, the
appropriate electrical signal is sent to keyboard
controller containing the ASCII value that particular
key.
For example the electrical signal that is generated
when keyboard key a is pressed, carry information of
digit 97 in the form of 0 and 1, which is the ASCII
value of character a.

15. Comparison
element
Analog signal Digital signal
Analysis Difficult Possible to analyze
Representation Continuous Discontinuous
Accuracy More accurate Less accurate
Storage Infinite memory Easily stored
Subject to
Noise
Yes No
Recording
Technique
Original signal is preserved Samples of the signal are taken
and preserved
Examples Human voice,
Thermometer, Analog
phones e.t.c
Computers, Digital Phones, Digital
pens, e.t.c
Difference between analog and digital signals

16. Conversion of analog to digital signals
• Since there are lot of concepts related to this analog
to digital conversion and vice-versa.
• There are two main concepts that are involved in the
conversion.
 Sampling
 Quantization

17. Sampling
Sampling
Sampling as its name suggests can be defined as take
samples.
Take samples of a digital signal over x axis. Sampling is
done on an independent variable.
Sampling is done on the x variable.

18. Quantization
Quantization as its name suggest can be defined as
dividing into quanta (partitions). Quantization is done
on dependent variable.
In case of this mathematical equation y = sin(x)
Quantization is done on the Y variable.
EE-2027 SaS, L1 18/20

19. Signal in Time and Frequency Domain
Time domain refers to variation of amplitude of signal with time.
For example consider a typical Electro cardiogram (ECG). If the doctor
maps the heartbeat with time say the recording is done for 20
minutes, we call it a time domain signal.
However, as in ECG a number of peaks are there (of different types).
Say in one heartbeat 4 types of peaks or variation in amplitude
occurs.
So in frequency domain, over the entire time period of recording, how
many times each peak comes is recorded.
Frequency is nothing but the number of times each event has occurred
during total period of observation.
Frequency domain analysis is much simple as you can figure out the
key points in the total interval rather than putting your eye on every
variation which occurs in time domain analysis.