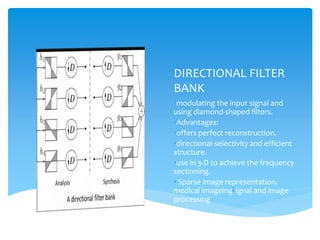
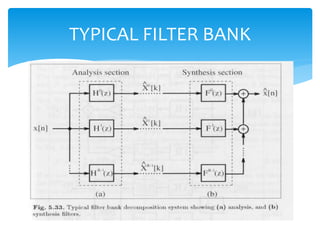
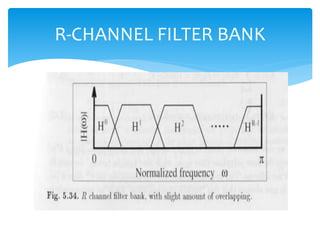
This document discusses filter banks, which are arrays of bandpass filters that separate an input signal into multiple sub-band components. It covers types of filter banks like analysis and synthesis banks, as well as uniform and non-uniform filter banks. Two-channel and polyphase two-channel filter banks are explained in more detail. Applications like signal compression and graphic equalizers are also mentioned. Lifting approaches for implementing filters efficiently are briefly outlined.

1. FILTER BANKS
By
SANJANA PRASAD
1601RL01
PhD –Full Time Research
scholar
PSG COLLEGE OF TECHNOLOGY

2.  INTRODUCTION TO FILTER BANKS
 TYPES OF FILTER BANKS
 UNIFORM DFT FILTER BANK
 TWO CHANNEL FILTER BANK
 POLYPHASE TWO CHANNEL FILTER BANK
 SUMMARY
 REFERENCES
TOPICS

3.  Array of BPF that seperates the input signal into
multiple components, each one carrying a single
sub-band of the original signal.
 A Digital filter bank is a collection of filters having
a common input or output.
2 types of filter banks
 Analysis filter bank
 Synthesis filter bank
INTRODUCTION

5. 1-D AND 2-D FILTER BANKS
1-D FILTER BANK 2-D FILTER BANK

6. MULTIDIMENSIONAL ANALYSIS AND
SYNTHESIS FILTER BANKS

7. DIRECTIONAL FILTER
BANK
•modulating the input signal and
using diamond-shaped filters.
•Advantages:
•offers perfect reconstruction.
•directional-selectivity and efficient
structure.
•use in 3-D to achieve the frequency
sectioning.
• Sparse image representation,
medical imageing[ ignal and image
processing

8. MULTI-DIMENSIONAL FILTER BANK

9.  Decomposition performed by the filter bank is called analysis
 Output of analysis - >subband signal
The Analysis filter may be
 non-overlapping,
 slightly overlapping
 substantially overlapping.
APPLICATION OF ANALYSIS FILTER BANKS:
 Spectrum analysis. (split the input signal into R different so
– called subband signals)
ANALYSIS FILTER BANKS

10.  Synthesis (i.e. recombining the outputs of multiple receivers)
INVOLVES:
 upsampling each one at a rate with the total bandwidth to be
created,
 translating each channel to its new center frequency, and
summing the streams of samples.
 Interpolation filter +Upsampling -> Synthesis filter.
 The combination of several signal into a common output signal is
called a Synthesis filter bank.
 The reconstruction process is called synthesis, meaning
reconstitution of a complete signal resulting from the filtering
process.
SYNTHESIS FILTER BANKS

11. Important characteristic of filter banks
 Bandwidth and spacing of the center frequencies of the
filters.
FILTER BANKS
UNIFORM FILTER BANKS
 same bandwidth and same sampling rates
NON UNIFORM FILTER BANKS
 Different bandwidth and different sampling rates
 Uniform, maximal decimation filter banks are often
preferred .
OTHER FILTER BANK TYPES

12. TYPICAL FILTER BANK

13. DFT filter bank :
 If the rth band filter hr[n] is computed from the
“modulation” of a single prototype filter h[n]
 A DFT filter interpolation R = Number of bands K
Applications Of Filter Banks
 Sub-band Adaptive Filtering
 Transmultiplexers
 Graphic Equalizer
 Signal Compression
 Vocoder
UNIFORM DFT FILTER BANK

14. R-CHANNEL FILTER BANK

15. ℎ 𝑟 𝑛 = ℎ 𝑛 𝑊𝑅
𝑟𝑛
= ℎ[𝑛]𝑒−𝑗2𝜋𝑟𝑛/𝑅
 An efficient implementation of the R channel filter bank can be
generated using polyphasedecomposition of the filter ℎ 𝑟[𝑛]
and the input signal 𝑧[𝑛].
 Because each of these bandpass filter is critically sampled, we
use a decomposition with R polyphase signals according to
ℎ 𝑛 =
𝑘=0
𝑅−1
ℎ 𝑘 𝑛 ↔ ℎ 𝑘 𝑚 = ℎ[𝑚𝑅 − 𝑘]
𝑥 𝑛 =
𝑘=0
𝑅−1
𝑥 𝑘 𝑛 ↔ 𝑥 𝑘 𝑚 = 𝑥[𝑚𝑅 − 𝑘]

16. ANALYSIS DFT FILTER BANK FOR
CHANNEL K

17. DFT ANALYSIS FILTER BANK DFT SYNTHESIS FILTER BANK

18. 𝑓 𝑟
𝑛 =
1
𝑅
𝑓 𝑛 𝑊𝑅
𝑟𝑛
= 𝑓[𝑛]𝑒 𝑗2𝜋𝑟𝑛/𝑅
If we now combine the analysis and synthesis filter banks,
we can see that the DFT and IDFT annihilate each other, and
perfect reconstruction occurs if the convolution of the
included polyphase filter gives a unit sample function, i.e.,
ℎ 𝑟 𝑛 × 𝑓𝑟 𝑛 =
1
0
𝑛 = 𝑑
𝑒𝑙𝑠𝑒
In other words, the two polyphase functions must be
inverse filters of each other, i.e.,
𝐻𝑟 𝑧 × 𝐹𝑟 𝑧 = 𝑧−𝑑
𝐹𝑟 𝑧 =
𝑧−𝑑
𝐻𝑟(𝑧)
Where we allow a delay d in order to have casual
(realizable) filters. These ideal conditions cannot be met
exactly by two FIR filters.

19. 
TWO-CHANNEL FILTER BANKS

20. STRUCTURE OF A TWO-CHANNEL
FILTER BANK

21.  The construction rule is normally given by
ℎ 𝑛 = (−1) 𝑛 𝑔 𝑛 ⊶ 𝐻 𝑧 = 𝐺 −𝑧
 For the synthesis use an expander (a sampling rate
increase of 2), and then two separate reconstruction
filters, 𝐺^ 𝑧 and 𝐻^ 𝑧 ,to reconstruct 𝑥[𝑛].
 A perfectly reconstructed signal has the sample shape
as the original, up to a phase (time) shift.
CONTD…

23. 2-CHANNEL QMF BANK
BLOCK OF A 2-CHANNEL
QMF BANK
FREQUENCY RESPONSE

24. 1. Run-length filter using short Winograd convolution
algorithms
2. Fast convolution using FFT
3. Using advanced arithmetic concepts such as
distribute arithmetic, reduced adder graph, or
residue number system
VARIOUS METHODS TO IMPLEMENT
L/2 FILTERS

25.  Constructs fast and efficient two-channel filter banks
 The basic idea is the use of cross-terms (called lifting
and dual lifting), as in a lattice filter, to construct a
longer filter from short filter, while preserving the
perfect reconstruction conditions
LIFTING

26.  Thus we have discussed about Analysis and Synthesis
filter banks,Uniform DFT and Non-uniform filter
banks
 Two channel filter banks /Polyphase two-channel filter
bank.
 Lifting approach has been listed out briefly.
Summary

27.  Digital Signal Processing With Field Programmable
Gate Arrays By Uwe Meyer Baese
 https://en.wikipedia.org/wiki/Filter_bank
REFERENCES