Dsp manual

DIGITAL SIGNAL PROCESSING [2171003]
Lab Manual 2016
Name:
Enrollment No. :

CONTENTS
Practical
No.
Aim
Page
No.
Sign.
1(a) w.a.p. to generate sin, cos, sinc and
exponential sequences
3
1(b) w.a.p to generate impulse, unit and ramp
signals.
4
2 w.a.p. for convolution and deconvolution of
given sequence.
5
3 w.a.p. to fold the given sequence. 6
4 w.a.p to find out even and odd function
from the given signal.
7
5(a) w.a.p. to find out transfer function of the
system from zeros and poles.
8
5(b) w.a.p. to find zeros and poles from
Transfer function and plot them on z-
plane.
9
6 w.a.p. to find out z-transform of given
sequences.
11
7 w.a.p. for up sampling and down sampling
of sequence.
12
8 w.a.p. to design IIR filter for analog filter
using butterworth, chebychev1,
chebychev2 and using elliptical.
13
9 Design FIR filter and make use of
(a) Kaiser window
(b) Hamming window
(c) Blackman window
15
10 Design FIR filter using FDA tools. 18
11 To Study Analog to Digital Filter
Transformation.
22
12 To study about TMS320C6713 DSK
processor.
25

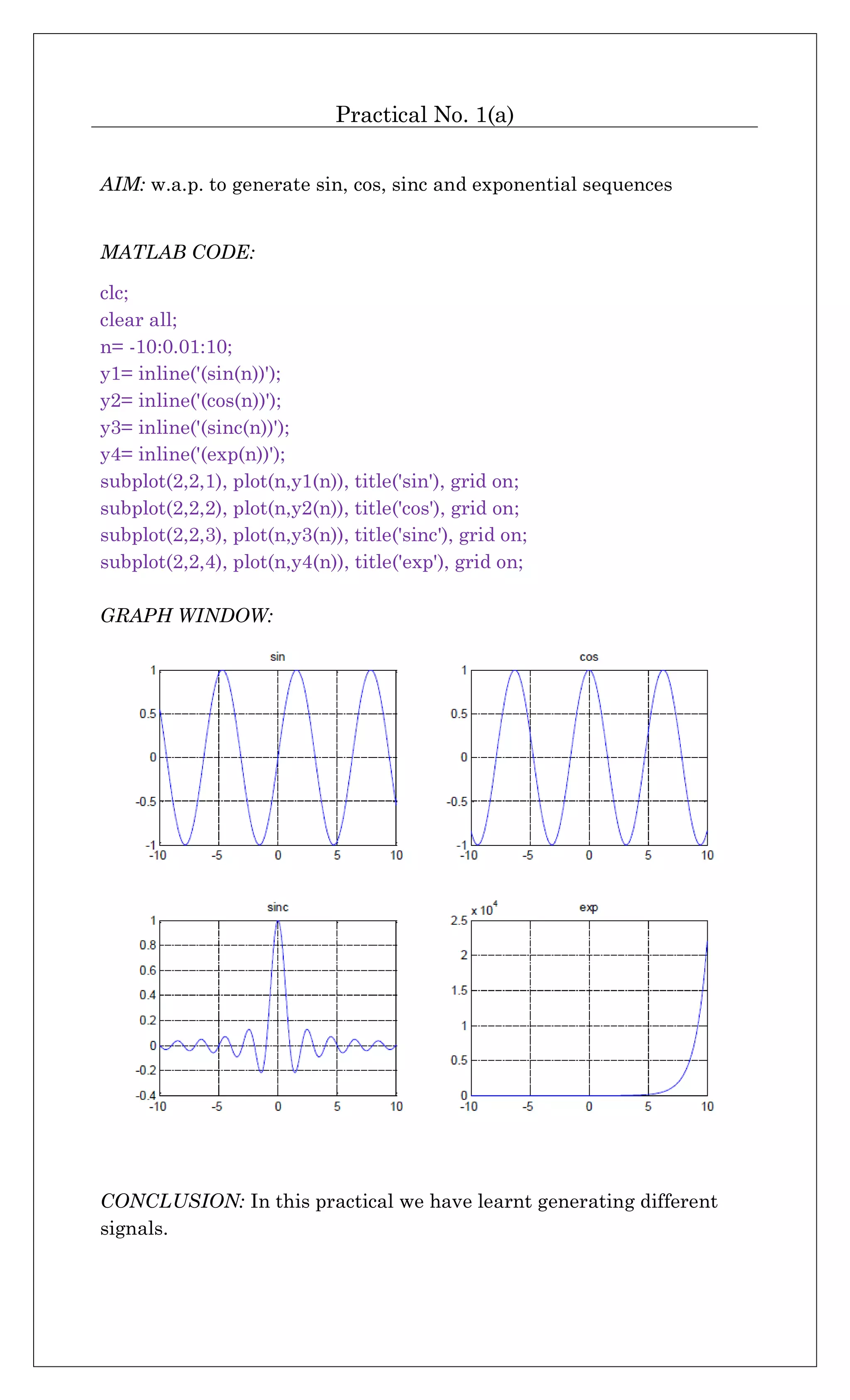
Practical No. 1(a)
AIM: w.a.p. to generate sin, cos, sinc and exponential sequences
MATLAB CODE:
clc;
clear all;
n= -10:0.01:10;
y1= inline('(sin(n))');
y2= inline('(cos(n))');
y3= inline('(sinc(n))');
y4= inline('(exp(n))');
subplot(2,2,1), plot(n,y1(n)), title('sin'), grid on;
subplot(2,2,2), plot(n,y2(n)), title('cos'), grid on;
subplot(2,2,3), plot(n,y3(n)), title('sinc'), grid on;
subplot(2,2,4), plot(n,y4(n)), title('exp'), grid on;
GRAPH WINDOW:
CONCLUSION: In this practical we have learnt generating different
signals.

Practical No. 1(b)
AIM: w.a.p to generate impulse, unit and ramp signals.
MATLAB CODE:
clc;
clear all;
n= -20:20;
i= 1.*(n==0);
u=1.*(n>=0);
r=n.*(n>=0);
subplot(3,1,1), stem(n,i), title('impulse');
subplot(3,1,2), stem(n,u), title('unit');
subplot(3,1,3), stem(n,r), title('ramp');
GRAPH WINDOW:
CONCLUSION: In this practical we have learnt generating different
discrete signals.

Practical No. 2
AIM: w.a.p. for convolution and deconvolution of given sequence.
MATLAB CODE:
clc;
clear all;
x= input('enter x:');
h= input('enter h:');
c= conv(x,h);
display('output by conv is:'); c
d= deconv(c,h);
display('output after deconvolution is:'); d
COMMAND WINDOW:
enter x:[1 2 5 3 6]
enter h:[2 6]
output by conv is:
c =
2 10 22 36 30 36
output after deconvolution is:
d =
1 2 5 3 6
>>
CONCLUSION: In this practical we have learnt about functions ‘conv’
and ‘deconv’ for convolution and deconvolution.

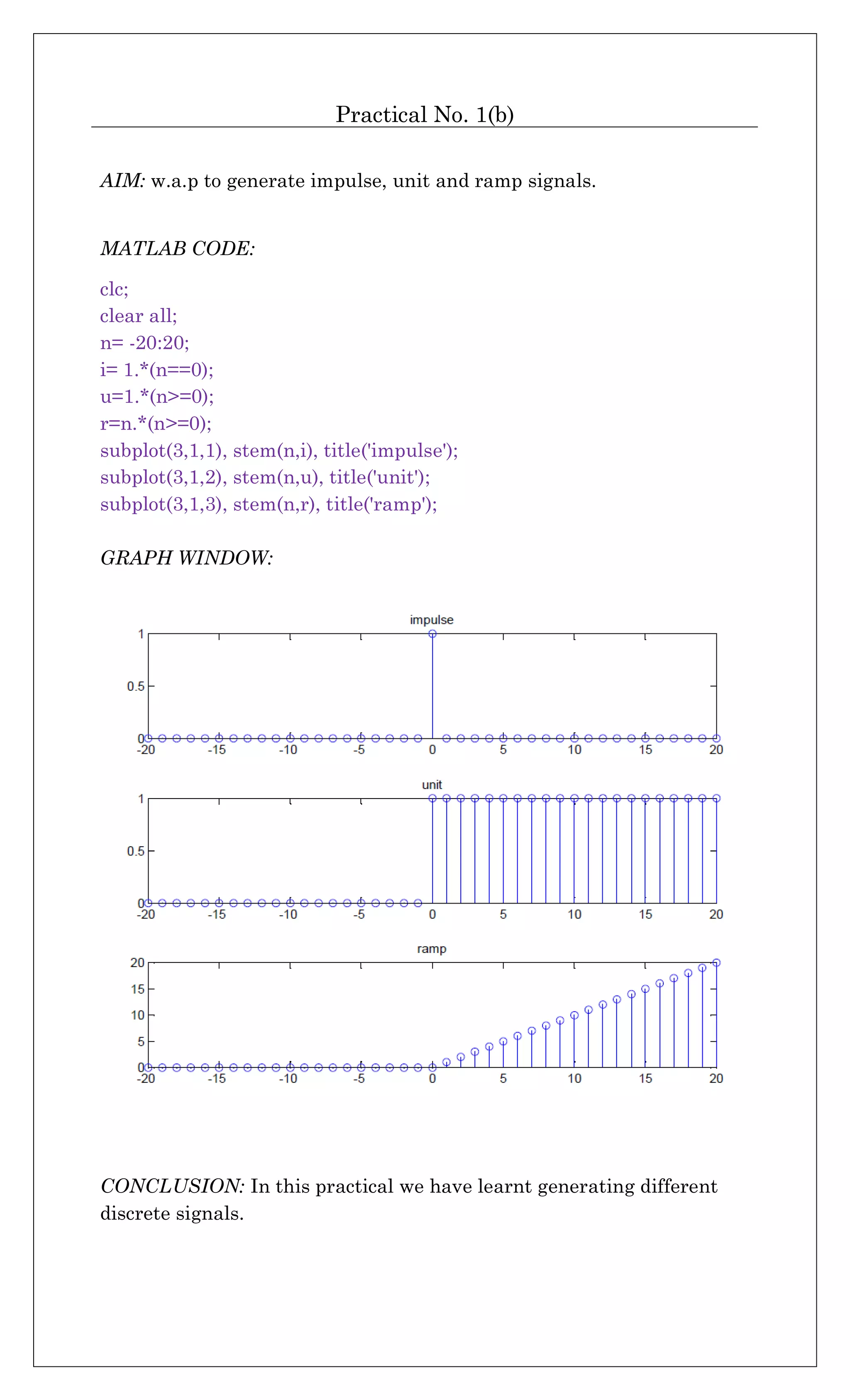
Practical No. 3
AIM: w.a.p. to fold the given sequence.
MATLAB CODE:
clc;
clear all;
n= [1 2 3 4 5 6];
a= [4 2 5 6 9 7];
subplot(2,1,1), stem(n,a), grid('on'), title('input');
n1= -fliplr(n);
a1= fliplr(a);
subplot(2,1,2), stem(n1,a1), grid('on'), title('output');
GRAPH WINDOW:
CONCLUSION: In this practical we have learnt about using ‘fliplr’
command for folding of sequences.

Practical No. 4
AIM: w.a.p to find out even and odd function from the given signal.
MATLAB CODE:
clc;
clear all;
n= sym('n');
x= inline('(cos(n))')
display('even function is:')
xe= (x(n)+x(-n))/2
display('odd function is:')
xo= (x(n)-x(-n))/2
COMMAND WINDOW:
x =
Inline function:
x(n) = (cos(n))
even function is:
xe =
cos(n)
odd function is:
xo =
0
>>
CONCLUSION: In this practical we have generated the even and odd
signals of the original signal.

Practical No. 5(a)
AIM: w.a.p. to find out transfer function of the system from zeros and poles.
MATLAB CODE:
clc;
clear all;
z= input('enter zeros as column vector:')
p= input('enter poles as row vector:')
k= input('enter gain in square bracket:')
[num den]=zp2tf(z,p,k);
display('tansfer function is:')
printsys(num,den,'s')
COMMAND WINDOW:
enter zeros as column vector:[1;2]
z =
1
2
enter poles as row vector:[1 3 2]
p =
1 3 2
enter gain in square bracket:[1]
k =
1
tansfer function is:
num/den =
s^2 - 3 s + 2
----------------------
s^3 - 6 s^2 + 11 s - 6
>>
CONCLUSION: In this
practical we have used
command ‘zp2tf’ for getting
transfer function from zeros
and poles.

Practical No. 5(b)
AIM: w.a.p. to find zeros and poles from Transfer function and plot them
on z-plane.
MATLAB CODE:
clc;
clear all
num= input('enter num co-efficient as row vector:');
den= input('enter den co-efficient as row vector:');
[z p k]=tf2zp(num,den)
zplane(num, den)
COMMAND WINDOW:
enter num co-efficient as row vector:[1 2]
enter den co-efficient as row vector:[1 3 2]
z =
-2
p =
-2
-1
k =
1
>>

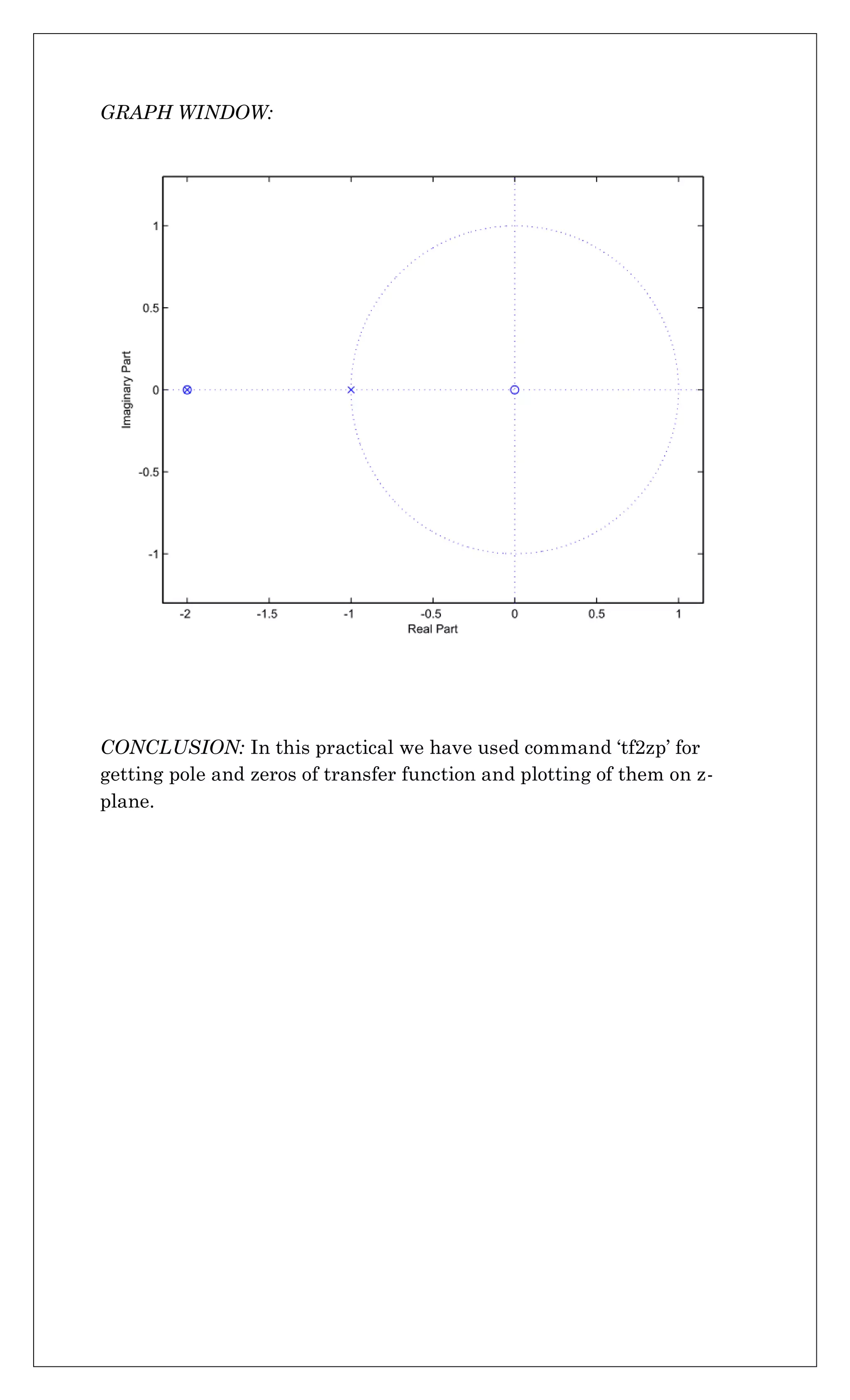
GRAPH WINDOW:
CONCLUSION: In this practical we have used command ‘tf2zp’ for
getting pole and zeros of transfer function and plotting of them on z-
plane.

Practical No. 6
AIM: w.a.p. to find out z-transform of given sequences.
MATLAB CODE:
clc;
clear all;
n= sym('n');
x= input('enter function in terms of n:')
display('z transform is:')
y= ztrans(x)
COMMAND WINDOW:
enter function in terms of n:2^n
x =
2^n
z transform is:
y =
z/(z - 2)
>>
CONCLUSION: In this practical we have used command ‘ztrans’ for finding
of z-transformation of the sequence.

Practical No. 7
AIM: w.a.p. for up sampling and down sampling of sequence.
MATLAB CODE:
clc;
clear all;
x= input(' enter sequence:')
a= input(' sample factor:')
u= upsample(x,a)
d= downsample(x,a)
COMMAND WINDOW:
enter sequence:[1 7 3 6 4 9]
x =
1 7 3 6 4 9
sample factor:2
a =
2
u =
1 0 7 0 3 0 6 0 4 0 9 0
d =
1 3 4
>>
CONCLUSION: In this practical we have used command ‘upsample’ and
‘downsample’ for up and down sampling of the sequence.

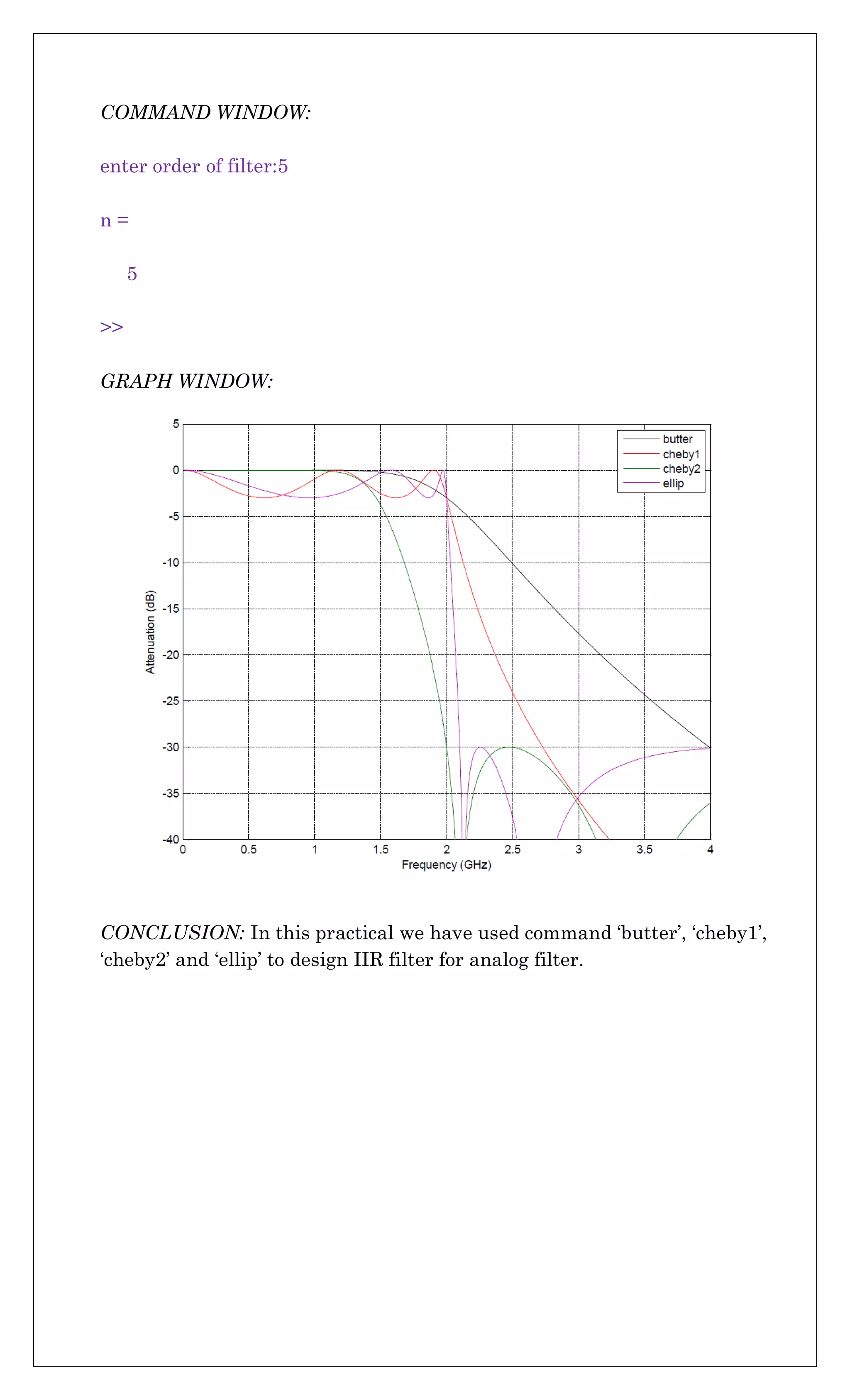
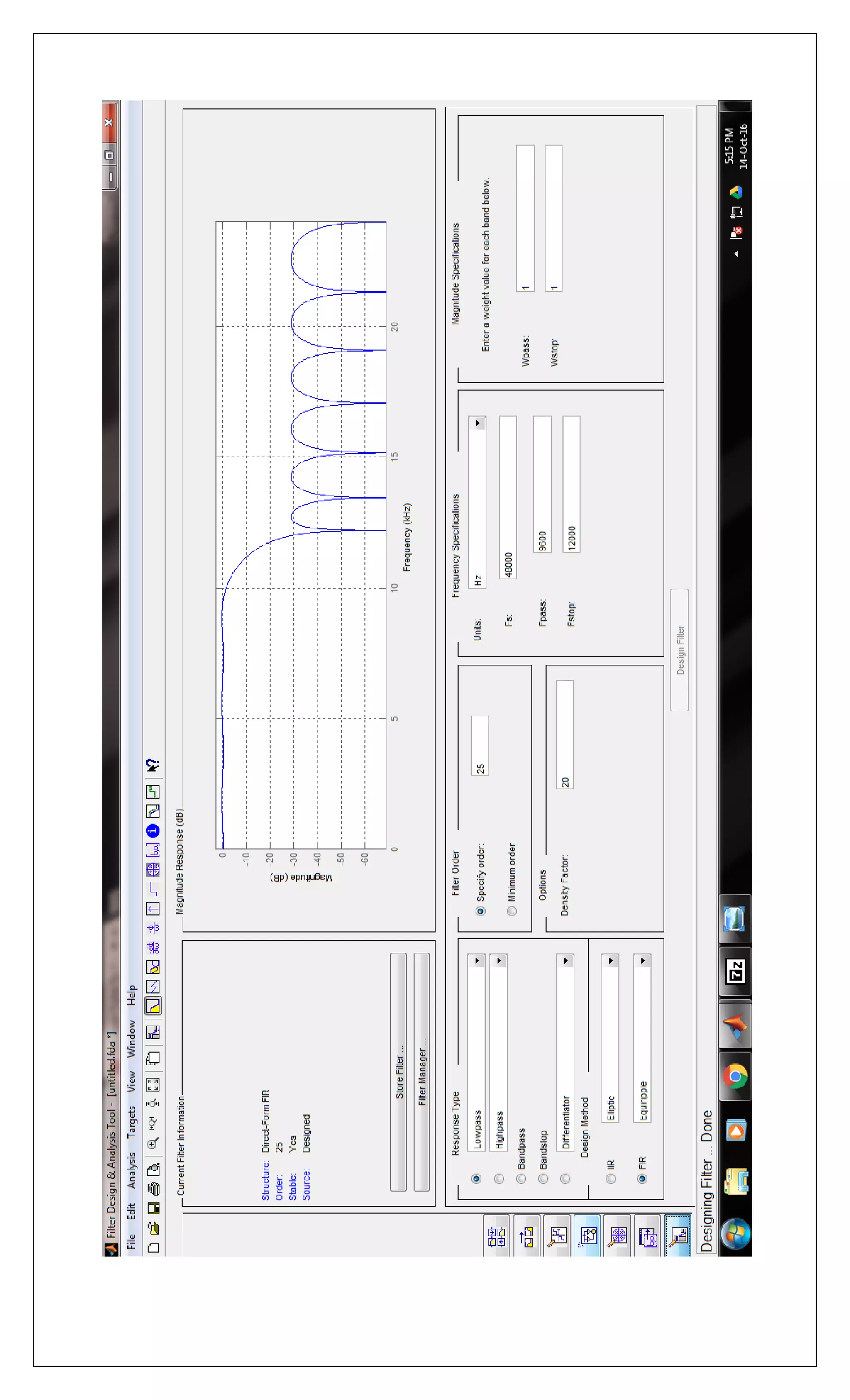
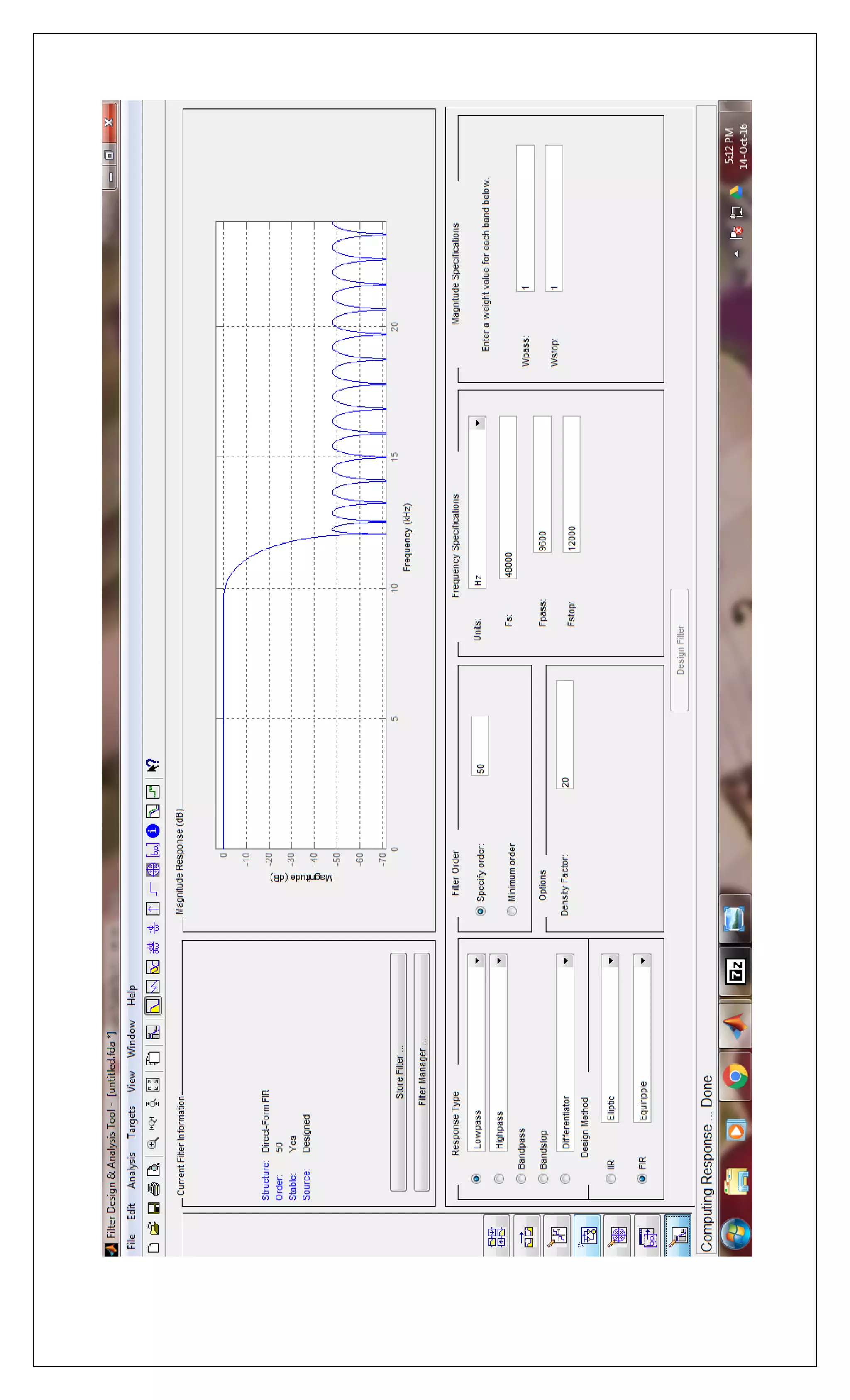
Practical No. 8
AIM: w.a.p. to design IIR filter for analog filter using butterworth,
chebychev1, chebychev2 and using elliptical.
MATLAB CODE:
clc;
clear all;
n = input('enter order of filter:')
f = 2e9;
[zb,pb,kb] = butter(n,2*pi*f,'s');
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,4096);
[z1,p1,k1] = cheby1(n,3,2*pi*f,'s');
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,4096);
[z2,p2,k2] = cheby2(n,30,2*pi*f,'s');
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,4096);
[ze,pe,ke] = ellip(n,3,30,2*pi*f,'s');
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,4096);
plot(wb/(2e9*pi),mag2db(abs(hb)))
hold on
plot(w1/(2e9*pi),mag2db(abs(h1)))
plot(w2/(2e9*pi),mag2db(abs(h2)))
plot(we/(2e9*pi),mag2db(abs(he)))
axis([0 4 -40 5])
grid on
xlabel('Frequency (GHz)')
ylabel('Attenuation (dB)')
legend('butter','cheby1','cheby2','ellip')

COMMAND WINDOW:
enter order of filter:5
n =
5
>>
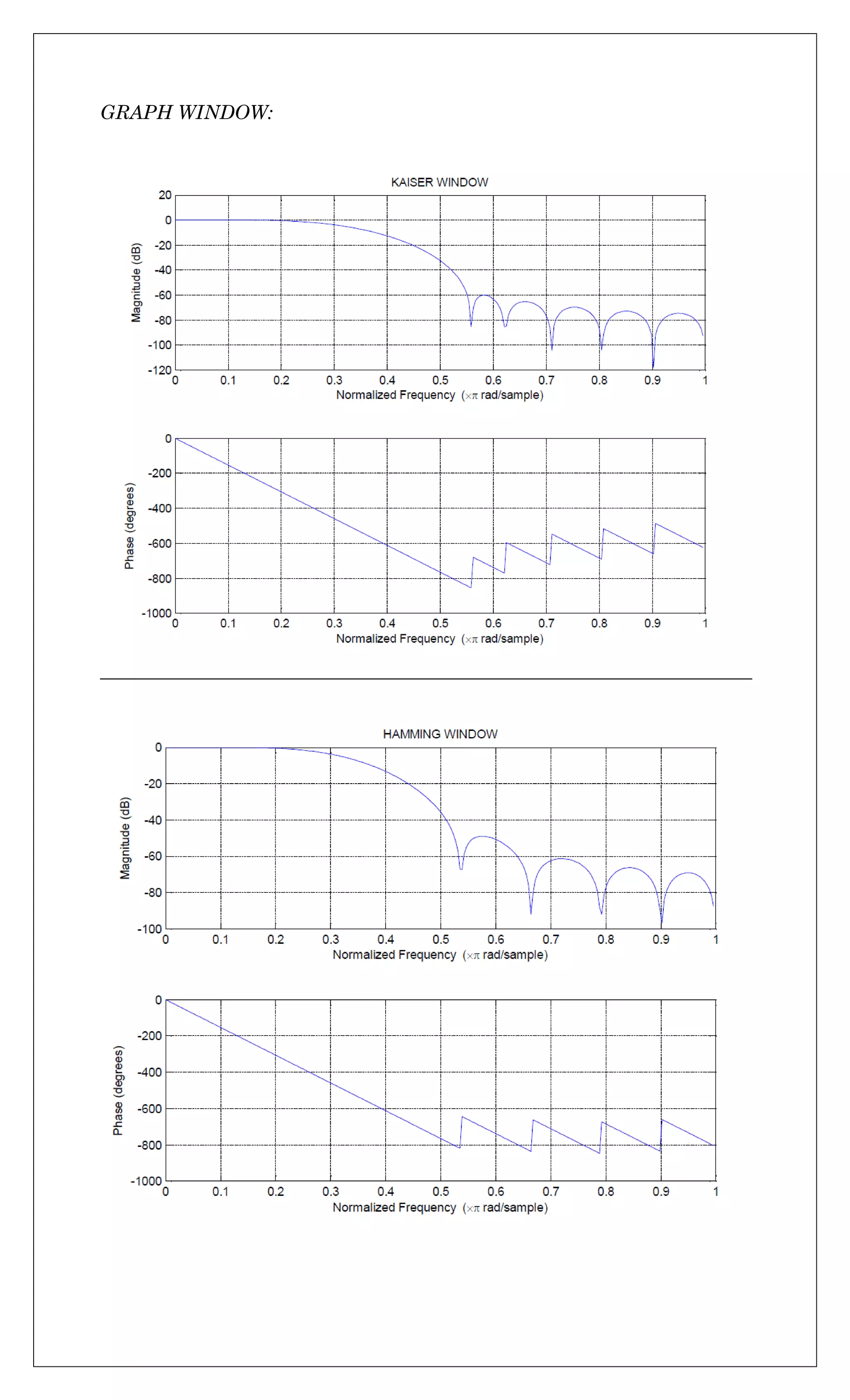
GRAPH WINDOW:
CONCLUSION: In this practical we have used command ‘butter’, ‘cheby1’,
‘cheby2’ and ‘ellip’ to design IIR filter for analog filter.

Practical No. 9
AIM: Design FIR filter and make use of
(a)Kaiser window
(b)Hamming window
(c) Blackman window
MATLAB CODE:
%FIR FILTER DESIGN
clc;
clear all;
close all;
pr=0.05;sr=0.04;
pf=1500;sf=2000;
f=9000;
wp=2*pf/f;ws=2*sf/f;
%LOW PASS FILTER
N=(-20*log10(sqrt(pr*sr))-13)/(14.6*(sf-pf)/f);
N=ceil(N);
%KAISER WINDOW
beta=5.8;
y=kaiser(N,beta);
b=fir1(N-1,wp,y);
figure(1);
freqz(b,1,256);
title('KAISER WINDOW');
%HAMMING WINDOW
y=hamming(N);
b=fir1(N-1,wp,y);
figure(2);
freqz(b,1,256);
title('HAMMING WINDOW');
%BLACKMAN WINDOW
y=blackman(N);
b=fir1(N-1,wp,y);
figure(3);
freqz(b,1,256);
title('BLACKMAN WINDOW');

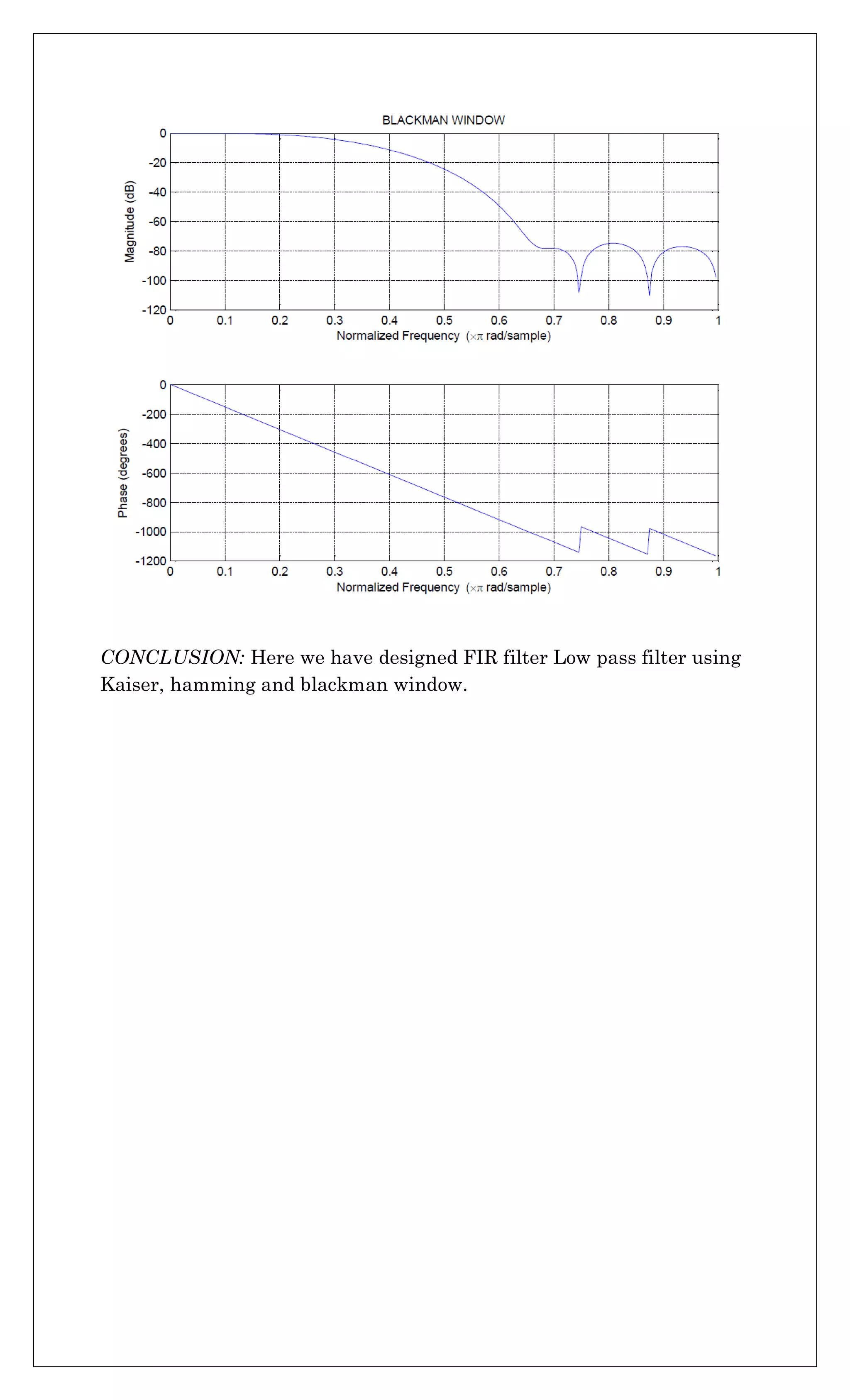
CONCLUSION: Here we have designed FIR filter Low pass filter using
Kaiser, hamming and blackman window.

Practical No. 10
AIM: Design FIR filter using FDA tools.
COMMAND WINDOW:
>> fdatool
>>
GRAPH WINDOW:
on next three pages.
CONCLUSION: In this practical we opened fda tool and learnt how to change
filter parameters manually.

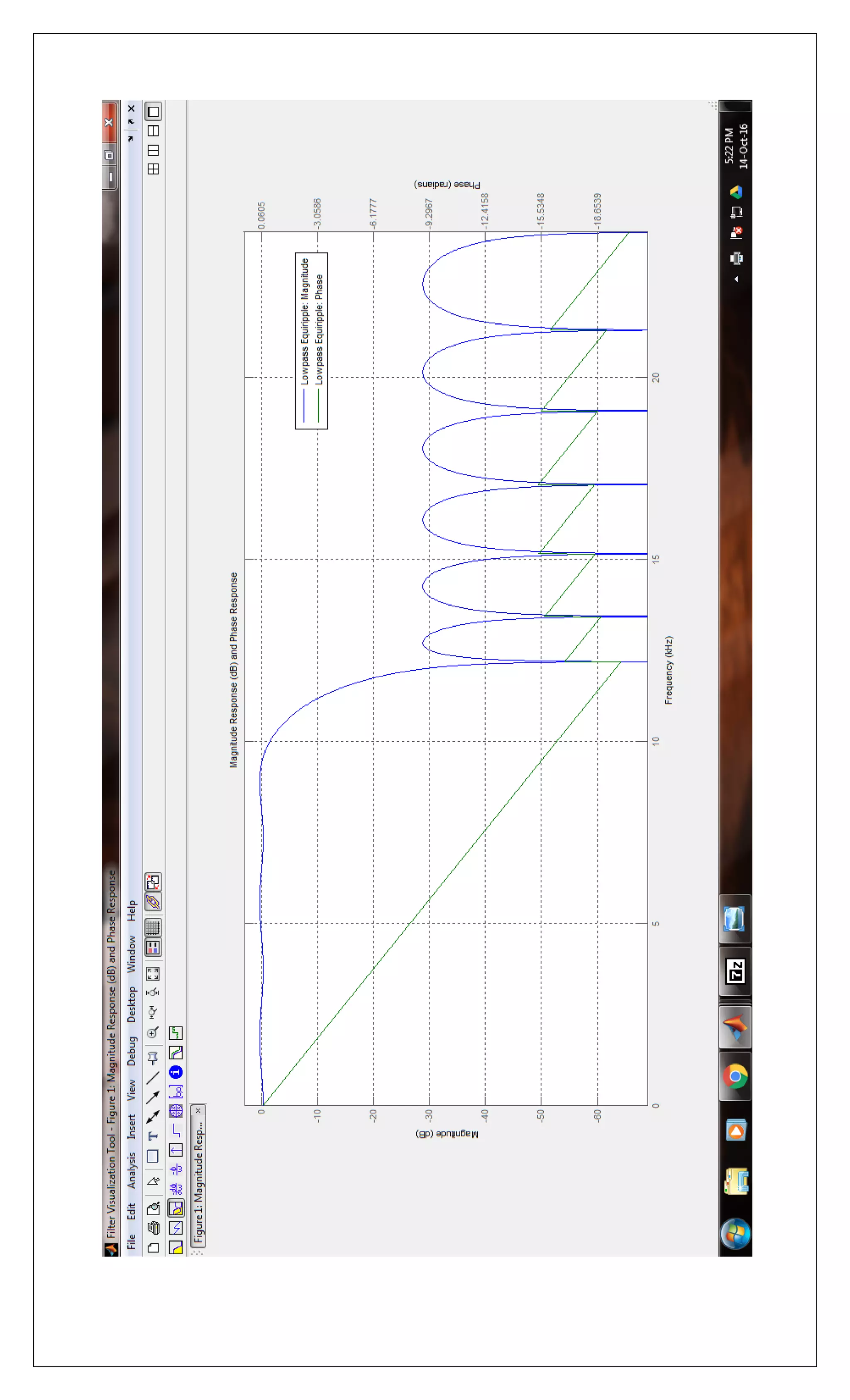
EXPERIMENT No.11
AIM: To Study Analog to Digital Filter Transformation.
1) Use impinvar to perform analog to digital filter transformation of
Take T=1s.
2) Use bilinear to perform analog to digital transformation of
Take Ts = 0.1s.
Description:
 The classic IIR filter design technique includes the following steps.
1) Find a high pass filter with cutoff frequency of 1 and translate this
prototype filter to the desired band configuration.
2) Transform the filter to the digital domain.
3) Discretize the filter
 Matlab functions can be used for filter designing are as below:
1) Impinvar [by, az] = impinvar (b, a, fs) creates a digital filter with numerator
and denominator coefficients bz and az, respectively, whose impulse
response is equal to the impulse response of the analog filter with
coefficients b and a, scaled by 1/fs. If we leave out the argument fs, or
specify fs as the empty vector [], it takes the default value of 1 Hz.
2) Bilinear -[numd,dend] = bilinear(num,den,fs) converts an s-domain transfer
function given by num and den to a discrete equivalent. Row vectors num
and den specify the coefficients of the numerator and denominator,
respectively, in descending powers of s. fs is the sampling frequency in
hertz. Bilinear returns the discrete equivalent in row vectors numd and dend
in descending powers of z (ascending powers of z-1).
Answer:
1) z = [1 0.2];
p = [1 0.4 9.04];
[num den]= impinvar(z,p,1);
sys= filt(num,den,1)
ffplot(sys)
Output:

2) z=[1];
p=[1 1];
[num den] = bilinear(z,p,10);
sys= filt(num,den,0.1)
ffplot(sys)

EXPERIMENT 12
Aim: To study about TMS320C6713 DSK processor.
Package Contents
 The C6713. DSK builds on TI’s industry-leading line of low cost, easy-to-use DSP
Starter Kit (DSK) development boards. The high-performance board features the
TMS320C6713 floating-point DSP. Capable of performing 1350 million floating-point
operations per second (MFLOPS), the C6713 DSP makes the C6713 DSK the most
powerful DSK development board.
 The DSK is USB port interfaced platform that allows to efficiently develop and test
applications for the C6713. The DSK consists of a C6713-based printed circuit board
that will serve as a hardware reference design for TI.s customers. products. With
extensive host PC and target DSP software support, including bundled TI tools, the
DSK provides ease-of-use and capabilities that are attractive to DSP engineers.
The C6713 DSK has a TMS320C6713 DSP onboard that allows full-speed verification of
code with Code Composer Studio. The C6713 DSK provides:

 A USB Interface
 SDRAM and ROM
 An analog interface circuit for Data conversion (AIC)
 An I/O port
 Embedded JTAG emulation support
The C6713 DSK includes a stereo codec. This analog interface circuit (AIC) has the
following characteristics:
 High-Performance Stereo Codec
 90-dB SNR Multibit Sigma-Delta ADC (A-weighted at 48 kHz)
 100-dB SNR Multibit Sigma-Delta DAC (A-weighted at 48 kHz)
 1.42 V . 3.6 V Core Digital Supply: Compatible With TI C54x DSP Core
Voltages
 2.7 V . 3.6 V Buffer and Analog Supply: Compatible Both TI C54x DSP
Buffer Voltages
 8-kHz . 96-kHz Sampling-Frequency Support
 Software Control Via TI McBSP-Compatible Multiprotocol Serial Port
 I 2 C-Compatible and SPI-Compatible Serial-Port Protocols
 Glueless Interface to TI McBSPs

 Audio-Data Input/Output Via TI McBSP-Compatible Programmable Audio Interface
 I 2 S-Compatible Interface Requiring Only One McBSP for both ADC and
DAC
 Standard I 2 S, MSB, or LSB Justified-Data Transfers
 16/20/24/32-Bit Word Lengths
The C6713DSK has the following features:
 The 6713 DSK is a low-cost standalone development platform that enables
customers to evaluate and develop applications for the TI C67XX DSP family. The
DSK also serves as a hardware reference design for the TMS320C6713 DSP.
Schematics, logic equations and application notes are available to ease hardware
development and reduce time to market.
 The DSK uses the 32-bit EMIF for the SDRAM (CE0) and daughtercard expansion
interface (CE2 and CE3). The Flash is attached to CE1 of the EMIF in 8-bit mode.
 An on-board AIC23 codec allows the DSP to transmit and receive analog signals.
 McBSP0 is used for the codec control interface and McBSP1 is used for data. Analog
audio I/O is done through four 3.5mm audio jacks that correspond to microphone
input, line input, line output and headphone output. The codec can select the
microphone or the line input as the active input. The analog output is driven to both
the line out (fixed gain) and headphone (adjustable gain) connectors.
 A programmable logic device called a CPLD is used to implement glue logic that ties
the board components together. The CPLD has a register based user interface that
lets the user configure the board by reading and writing to the CPLD registers.

 TMS320C6713 DSP Features:
 Highest-Performance Floating-Point Digital Signal Processor (DSP):
 Eight 32-Bit Instructions/Cycle
 32/64-Bit Data Word
 300-, 225-, 200-MHz (GDP), and 225-, 200-, 167-MHz (PYP) Clock
rates 3.3-, 4.4-, 5-, 6-Instruction Cycle Times
 2400/1800, 1800/1350, 1600/1200, and 1336/1000 MIPS /MFLOPS
 Rich Peripheral Set, Optimized for Audio
 Highly Optimized C/C++ Compiler
 Extended Temperature Devices Available
 Advanced Very Long Instruction Word (VLIW) TMS320C67x. DSP Core
 Eight Independent Functional Units:
 Two ALUs (Fixed-Point)
 Four ALUs (Floating- and Fixed-Point)
 Two Multipliers (Floating- and Fixed-Point)
 Load-Store Architecture With 32 32-Bit General-Purpose Registers
 Instruction Packing Reduces Code Size
 All Instructions Conditional
 Instruction Set Features
 Native Instructions for IEEE 754
 Single- and Double-Precision
 Byte-Addressable (8-, 16-, 32-Bit Data)
 8-Bit Overflow Protection
 Saturation; Bit-Field Extract, Set, Clear; Bit-Counting; Normalization
 L1/L2 Memory Architecture
 4K-Byte L1P Program Cache (Direct-Mapped)
 4K-Byte L1D Data Cache (2-Way)
 256K-Byte L2 Memory Total: 64K-Byte L2 Unified Cache/Mapped RAM,
and 192KByte additional L2 Mapped RAM
 Device Configuration
 Boot Mode: HPI, 8-, 16-, 32-Bit ROM Boot
 Endianness: Little Endian, Big Endian
 32-Bit External Memory Interface (EMIF)
 Glueless Interface to SRAM, EPROM, Flash, SBSRAM, and SDRAM
 512M-Byte Total Addressable External Memory Space
 Enhanced Direct-Memory-Access (EDMA) Controller (16 Independent
channels)
 16-Bit Host-Port Interface (HPI)
 Two Multichannel Audio Serial Ports (McASPs)
 Two Independent Clock Zones Each (1 TX and 1 RX)
 Eight Serial Data Pins Per Port:
 Individually Assignable to any of the Clock Zones
 Each Clock Zone Includes:
 Programmable Clock Generator
 Programmable Frame Sync Generator
 TDM Streams From 2-32 Time Slots
 Support for Slot Size:
 8, 12, 16, 20, 24, 28, 32 Bits
 Data Formatter for Bit Manipulation

 Wide Variety of I2S and Similar Bit Stream FormatsIntegrated Digital
 Audio Interface Transmitter (DIT) Supports:
 S/PDIF, IEC60958-1, AES-3, CP-430 Formats
 Up to 16 transmit pins
 Enhanced Channel Status/User Data
 Extensive Error Checking and Recovery
 Two Inter-Integrated Circuit Bus (I2C Bus.) Multi-Master and Slave Interfaces
 Two Multichannel Buffered Serial Ports:
 Serial-Peripheral-Interface (SPI)
 High-Speed TDM Interface
 AC97 Interface
 Two 32-Bit General-Purpose Timers
 Dedicated GPIO Module With 16 pins (External Interrupt Capable)
 Flexible Phase-Locked-Loop (PLL) Based Clock Generator Module
 IEEE-1149.1 (JTAG ) Boundary-Scan-Compatible
 Package Options:
 208-Pin PowerPAD. Plastic (Low-Profile) Quad Flatpack (PYP)
 272-BGA Packages (GDP and ZDP)
 0.13-µm/6-Level Copper Metal Process
 CMOS Technology
 3.3-V I/Os, 1.2 -V Internal (GDP & PYP)
 3.3-V I/Os, 1.4-V Internal (GDP)(300 MHz only)
Procedure to work on Code Composer Studio

1. To create a New Project
Project New (SUM.pjt)
2. To Create a Source file
File New

3. To Add Source files to Project
Project Add files to Project sum.c

4. To Add rts6700.lib file & hello.cmd:
Project Add files to Project rts6700.lib
Path: c:CCStudioc6000cgtoolslibrts6700.lib
Note: Select Object & Library in(*.o,*.l) in Type of files
Project Add files to Project hello.cmd
Path: c:titutorialdsk6713hello1hello.cmd
Note: Select Linker Command file(*.cmd) in Type of files
5. To Compile:
Project Compile File
6. To build or Link:
Project build,
Which will create the final executable (.out) file.(Eg. sum.out).
7. Procedure to Load and Run program:
Load program to DSK:

File Load program sum. out
8. To execute project:
Debug Run.
Program:
‘C’ Program to Implement Impulse response:
#include <stdio.h>
#define Order 2
#define Len 10
float y[Len]={0,0,0},sum;
main()
{
int j,k;
float a[Order+1]={0.1311, 0.2622, 0.1311};
float b[Order+1]={1, -0.7478, 0.2722};
for(j=0;j<Len;j++)
{
sum=0;
for(k=1;k<=Order;k++)
{
if((j-k)>=0)
sum=sum+(b[k]*y[j-k]);
}
if(j<=Order)
{
y[j]=a[j]-sum;
}
else
{

y[j]=-sum;
}
printf("Respose[%d] = %fn",j,y[j]);
}
}
‘C‘ Program to Implement Difference Equation
#include <stdio.h>
#include<math.h>
#define FREQ 400
float y[3]={0,0,0};
float x[3]={0,0,0};
float z[128],m[128],n[128],p[128];
main()
{
int i=0,j;
float a[3]={ 0.072231,0.144462,0.072231};
float b[3]={ 1.000000,-1.109229,0.398152};
for(i=0;i<128;i++)
{
m[i]=sin(2*3.14*FREQ*i/24000);
}
for(j=0;j<128;j++)
{
x[0]=m[j];
y[0] = (a[0] *x[0]) +(a[1]* x[1] ) +(x[2]*a[2]) - (y[1]*b[1])-
(y[2]*b[2]);
z[j]=y[0];
y[2]=y[1];
y[1]=y[0];
x[2]=x[1];

Dsp manual

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (20)

Similar to Dsp manual

Similar to Dsp manual (20)

More from Vijendrasingh Rathor

More from Vijendrasingh Rathor (6)

Recently uploaded

Recently uploaded (20)

Dsp manual