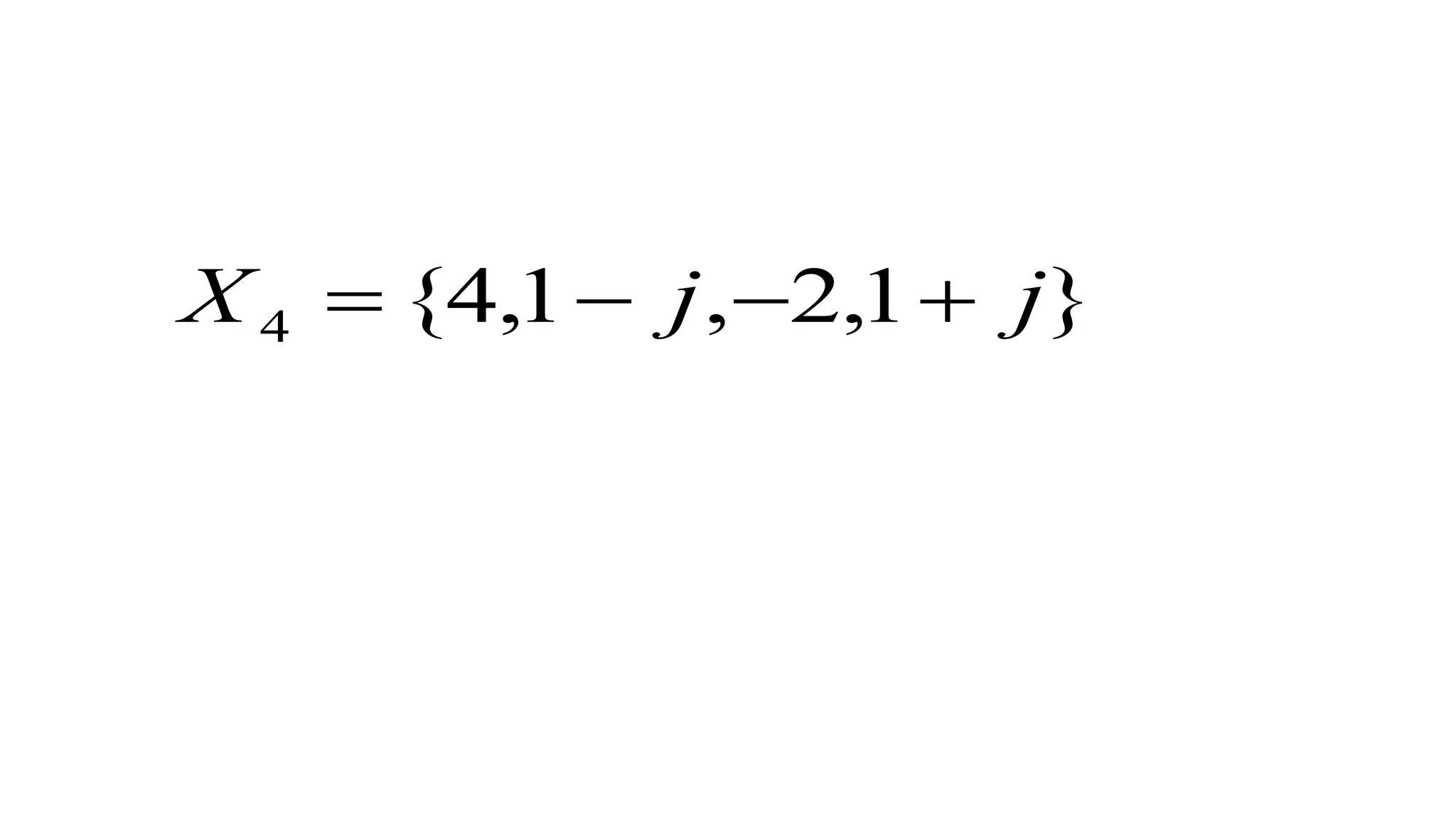![Matrix Relations:
• Where
NNN xWX ][=
−
=
)1(
.
.
.
)2(
)1(
)0(
NX
X
X
X
X N
DFT :](https://image.slidesharecdn.com/dft-slidesharr-181021101815/75/Computing-DFT-using-Matrix-method-7-2048.jpg)
![Ex.1] Find DFT of x(n)={1,2,0,1}
Solution: NNN xWX ][=
−−
−−
+−−
=
1
0
2
1
11
1111
11
1111
4
jj
jj
X](https://image.slidesharecdn.com/dft-slidesharr-181021101815/75/Computing-DFT-using-Matrix-method-8-2048.jpg)
Uploaded bySarang Joshi
Computing DFT using Matrix method
The document discusses calculating the discrete Fourier transform (DFT) using a matrix method. It involves representing the DFT as a matrix multiplication of an N×N twiddle factor matrix and an N×1 input vector. The twiddle factor matrix contains elements that are powers of the Nth root of unity. An example calculates the 4-point DFT of the vector [1, 2, 0, 1] by multiplying it by the twiddle factor matrix.
More Related Content
Similar to Computing DFT using Matrix method
Computing DFT using Matrix method
- 1. Calculating DFT usingMatrix method - SARANG JOSHI
- 2. • N-point DFT: • Twiddle factor: − = − = 1 0 2 )()( N n N n kj enxkX For k=0,1,2…..N-1 N j N eW 2 − = − = = 1 0 )()( N n kn NWnxkX For k=0,1,2…..N-1
- 3. = kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N kn N WWWW WWWW WWWW WWWW W ............ .......... .......... .......... ............. ............ ............. n=0 n=1 n=2………….. n=N-1 k=0 k=1 k=2 . . k=N-1 TWIDDLE FACTOR MATRIX
- 4.
- 5. = 1 2 0 2 0 2 0 2 2 WW WW W kn − = 11 11 2 kn W N j NeW 2 − = 2 2 2 j eW − = j 2 − = eW IdentitysEuler'...........)sin()cos( je j −=−
- 6.
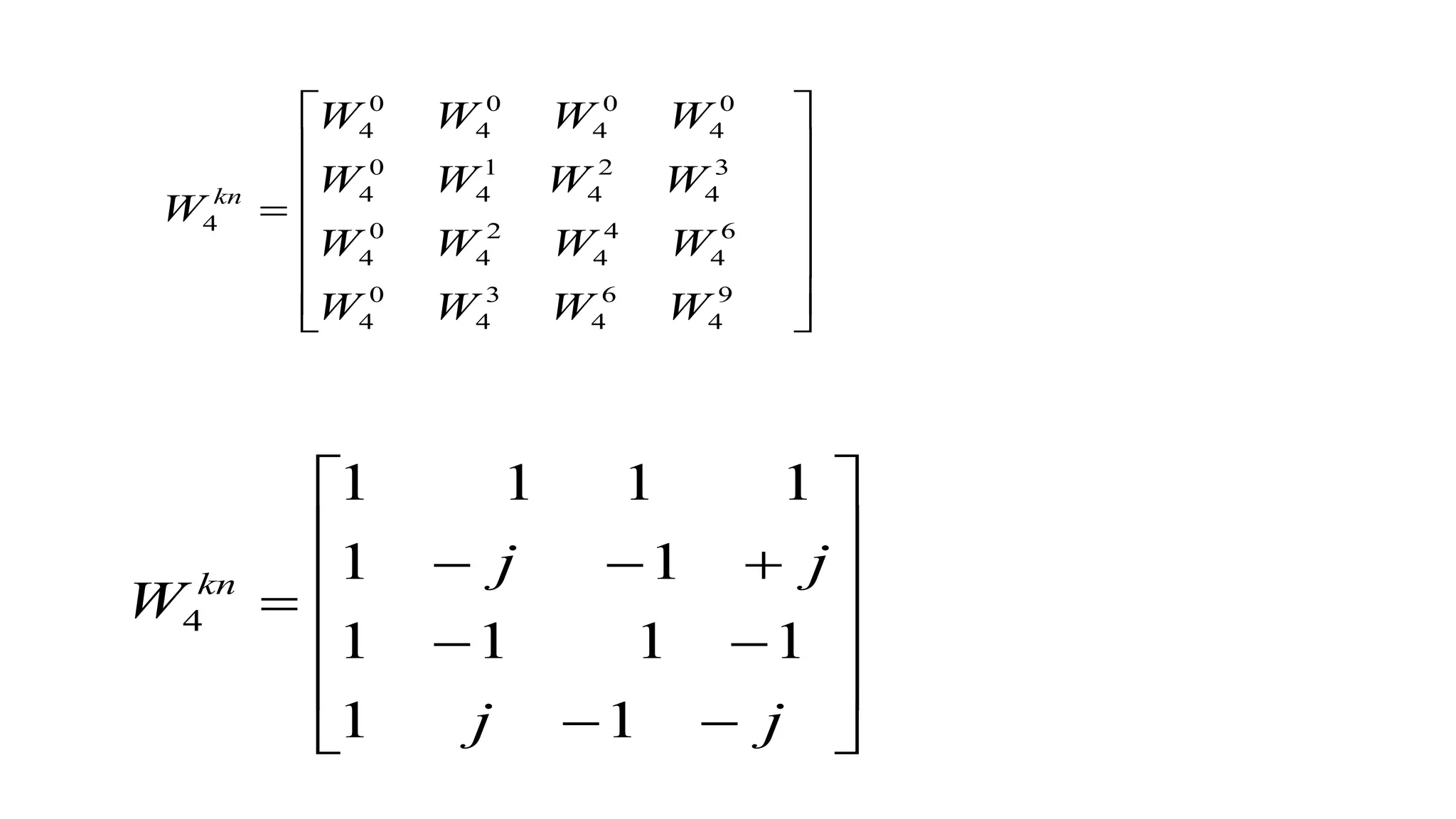
- 7. Matrix Relations: • Where NNNxWX ][= − = )1( . . . )2( )1( )0( NX X X X X N DFT :
- 8. Ex.1] Find DFTof x(n)={1,2,0,1} Solution: NNN xWX ][= −− −− +−− = 1 0 2 1 11 1111 11 1111 4 jj jj X
- 9.
- 10. RATE, FOLLOW &SHARE https://unacademy.com/user/jsarang70-7008
- 11.