This document provides an introduction to digital signal processing (DSP) through a lecture given by Prof. A.H.M. Asadul Huq. The lecture defines signals and discusses advantages and disadvantages of digital systems. It also outlines key DSP operations like convolution and correlation. Application areas are reviewed and basic elements of a DSP system are introduced. The document concludes by thanking attendees and providing a password to download the presentation.

1. DSP Lectures
ETE 315
INTRODUCTION
Prof. A.H.M. Asadul Huq, Ph.D.
http://asadul.drivehq.com/students.htm
asadul.huq@ulab.edu.bd
February 3, 2013 A.H. 1

2. INTRODUCTION
What is a Signal?
Any variable that carries or contains some kind of
information that can be conveyed, displayed or
manipulated.
• Analogue - Continuous
• Digital - Discrete, Digitized, Quantized
• Primary use of DSP
- Reduce interference, noise and other undesirable
components acquired in data.
February 3, 2013 A.H. 2

3. Advantage Vs. Disadvantages
Advantages of Digital Systems
• Guaranteed Accuracy
• Perfect Reproducibility
• Non-variant with Temperature and Age
• Greater Flexibility
• Superior Performance
• Most modern data is already in digital format
February 3, 2013 A.H. 3

4. Advantage Vs. Disadvantages
Disadvantages
• Speed and Cost ???
• Design Time
• Finite Wordlength
February 3, 2013 A.H. 4

5. Application Areas
Image Processing
• Pattern Recognition
• Computer/ Robotic Vision
Commercial
• Movie Special Effects
• Video Conferencing
Telecommunications
• Echo Cancellation
• Data Communications
February 3, 2013 A.H. 5

6. Application Areas
Speech/ Audio
• Speech Recognition
• Text to Speech
Military
• Radar/ Sonar Processing
• Missile Guidance
Consumer Applications
• Mobile Phones
• HDTV
February 3, 2013 A.H. 6

7. Application Areas
Instrumentation/ Control
• Noise Reduction
• Data Compression
Space
• Space Photograph Enhancement (Hubble etc.)
• Interplanetary Probes
Medical
• Ultrasound
ECG
February 3, 2013 A.H. 7

8. Basic Elements of DSP System
Fig. 1.3 [Proa]. Block diagram of a DSP System
02/03/13 15:00 8 A.H.

9. Characteristics of Practical Digital Signal
For a signal to be completely representable
and storable in a digital system-
• Discrete-Time
• Discrete-Valued
• Finite duration
• Finite number of discrete values
02/03/13 15:00 A.H. 9

10. Basic Parts of an A/D Converter [Proa P. 22]
Fig. Proa 1.14 (modified) Block diagram of A/D Converter
• Sampling: Convertd C-T signal into D-T signal by taking
“samples” of the C-T signal at D-T instants. At the point D we
obtain x(nTs)=x(n). Ts is called sampling interval
• Quantization: Converts C-V D-T signal into D-V D-T signal
(Digital signal xq at the point E). Diff between x(n) and xq(n) is
called quantization error [See more in Proakis 33].
02/03/13 15:00 10 A.H.

11. Coding and Sampling Theory
Coding: Converts xq(n) in to binary sequence
• Sampling Theorem:
If the frequency component in a signal is fmax ,
then the signal should be sampled at the rate
of at least 2fmax for the samples to describe the
signal completely. –
fs >= 2fmax
[See more in Proakis P.30]
11
02/03/13 15:00 A.H.

12. Effect of sampling period
02/03/13 15:00 A.H. 12

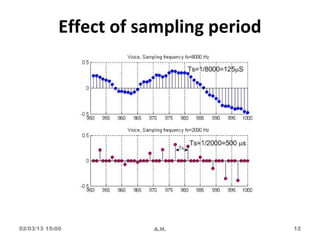
13. Wave-2
Wave-1 Wave-3
Listen to original sound at Fs = 8000 Hz in Normal
Tempo [Wave-1]
Listen to the sound at reduced Fs = 2000 Hz in Normal
Tempo [Wave-2]
Listen to the sound at Fs = 2000 Hz in fast tempo
[Wave-3].
Listen to the sound at Fs = 8000 Hz in SLOW tempo
02/03/13 15:00 A.H. 13

14. Simple Manipulations of D-T Signals [52]
Types of manipulations-
• Transformation of independent variables (time
index).
- Shifting: Delay, Advance
• Modification of dependent variable (amplitude
values).
Addition
Multiplication
Amplitude scaling
February 3, 2013 A.H. 14

15. Shifting [P.52]
x(n) y(n)=x(n-k)
Shift by k
Shift Operation –
• Shifting of a signal x(n) is moving of the signal along n
index. In the shifting process, the independent
variable n is replaced by n-k.
• Shift equation: y(n) = x(n-k), k is an integer
• 2 types of shift operations -
– Right shift – k is positive [Delay]
– Left shift – k is negative [Advance]
February 3, 2013 A.H. 15

16. Shift Example [P. 53]
• [a] x(n) = [-1 0 1 2 3 4 4 4 4 4]
• [b] x(n-3) = [-1 0 1 2 3 4 4 4 4 4] [Delayed]
• [c] x(n+2) = [-1 0 1 2 3 4 4 4 4 4] [Advanced]
February 3, 2013 A.H. 16

17. Fold
In this operation each sample of x(n) flips
around n=0.
Folding equation: y(n) = x(-n)
Note:
• Operation of Folding AND Shifting of a signal are not
commutative
i.e., TD{ FD[ (x) ] } ≠ FD{ TD[ (x) ] }.
≠
(See Proa 53 for proof)
February 3, 2013 A.H. 17

18. Fold Speech?
Original voice 
Folded voice 
February 3, 2013 A.H. 18

19. Fold and Shift Example
• [a] x(n) = [2 2 2 0 1 2 3 4]
• [b] x(-n) = [ 4 3 2 1 0 2 2 2 ] [Folded]
• [c] x(-n+2) = [ 4 3 2 1 0 2 2 2 ] [Folded and right
Shifted]
February 3, 2013 A.H. 19

20. Key DSP Operations
There are 5 basic DSP operations
• Convolution
• Correlation
• Filtering
• Transformation
• Modulation
February 3, 2013 A.H. 20

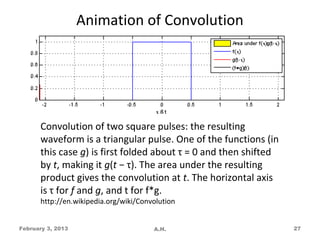
21. Convolution
• Definition:
Given 2 finite length sequences, x(n) and h(n),
their linear convolution is
y( n ) = x( n )* h( n )
∞
= ∑ x( k )h( n − k )
k = −∞
• Where the symbol [*] is used to denote
convolution
February 3, 2013 A.H. 21

22. The process of computing Convolution
To obtain y(n0) at some instant of time, n = n0
∞
y( n 0 ) = ∑ x( k )h( n 0 − k )
k = −∞
1. Fold h(k) about k=0 to obtain h(-k)
2. Shift h(-k) by n0 to the right to obtain h(n0–k)
3. Multiply x(k) by h(n0 –k) to obtain the product sequence
4. Sum all the elements of v to obtain y(n0)
To obtain y(n) [i.e., complete convolution output] -
Repeat steps 2-4 for all time shifts
February 3, 2013 A.H. 22

23. Example of computing Convolution
Problem Proa 2.3.2
Given, h(n)=[1,2,1,-1]; and x(n)=[1,2,3,1]
Compute the convolution output
y(n)=h(n)*x(n).
x(n) y(n)=x(n)*h(n)
h(n)
February 3, 2013 A.H. 23

24. Solution
General formula of convolution -
k =∝
y(n) = ∑ x(k)h(n − k)
k =−∝
Now, putting x(k) = {1,2,3,1} and h(k ) = {1, 2,1,−1}
↑ ↑
and folding h(k) about k = 0 we get, h(−k ) = {−1,1, 21}
↑
Now right shift h(-k) starting from n=0, multiply it with the
x(k) to get the product sequence, Then, the sum of all the
elements of the product sequence produces y(0)
February 3, 2013 A.H. 24

25. Solution … continued
For , n = 0
y(0) = ∑ x(k )h(0 − k ) and h(0 − k ) = {−1,1, 2,1}
↑
= ∑{1,2,3,1}{−1,1, 2,1}
↑ ↑
= ∑{0,0 1 ,2,3,1}{−1,1, 2,1,0,0}
↑ ↑
= (0 * −1) + (0 *1) + (1* 2) + (2 *1) + (3 * 0) + (1* 0)
=0+0+2+2+0+0
= −1
Now right shift h(-k), i.e. , calculate y(1) for n=1
February 3, 2013 A.H. 25

26. Solution …. continued
For n = 1
y (1) = ∑ x(k )h(1 − k ) and h(1 − k ) = {−1, 1 ,2,1}
↑
= ∑{1,2,3,1}{−1, 1 ,2,1}
↑ ↑
= (1*1) + (2 * 2) + (1* 3) + (0 *1) + (−1* 0)
=1+ 4 + 3 + 0 + 0 = 8
Now after completing all (left and right) shifts
of h(-k), we get – (i.e., For n=-1 to n=+5)
y(n) = { y(− ∝)... y(−4), y(−3), y(−2), y(−1), y(0), y(1),
↑
y(2), y(3), y(4), y(5), y(6), y(7),... y(∝)}
or , y(n) = {...0,0,1, 4,8,8,3,−2,−1,0,0,...}
↑
Note: Total number of elements in y(n) =
N=length of y(n)=length of x(n)+length of h(n)-1.
That is in this case N=4+4-1=7.
February 3, 2013 A.H. 26

27. Animation of Convolution
Convolution of two square pulses: the resulting
waveform is a triangular pulse. One of the functions (in
this case g) is first folded about τ = 0 and then shifted
by t, making it g(t − τ). The area under the resulting
product gives the convolution at t. The horizontal axis
is τ for f and g, and t for f*g.
http://en.wikipedia.org/wiki/Convolution
February 3, 2013 A.H. 27

28. Correlation [Proa 120]
• Correlation is an operation that enables the
measurement of the degree to which 2
sequences are similar
• There are 2 types of correlations -
1. Crosscorrelation
2. Autocorrelation
February 3, 2013 A.H. 28

29. Cross-correlation
∞
• Definition: rxy ( l ) = ∑ x( n )y( n − l )
n = −∞
•l = … -3,-2,-1,0,1,2,3, … Here, l is lag or shift
•x(n) is the reference
•y(n) shifts by l samples with respect to x(n)
•y(n) shifts right for +l
•y(n) shifts left for -l
Autocorrelation
∞
• Definition rxx ( l ) = ∑ x( n )x( n − l )
n = −∞
February 3, 2013 A.H. 29

30. Correlation example [Proa 120]
Example 2.6.1
Determine the cross-correlation sequence rxy (l) of
the sequences –
x(n) = {2,-1,3,7,1,2,-3}
y(n) = {1,1,-1,2,-2,4,1,-2,5}
February 3, 2013 A.H. 30

31. Solution to Problem
Compute rxy (0), for lag l=0
rxy (0) = ∑{2,−1,3,7 ,1,2,−3}{1,1,−1,2,−2, 4,1,−2,5}
↑ ↑
= 2 + 1 + 6 − 14 + 4 + 2 + 6
=7
For other values of l, simply shift y(n) to the right and left
relative to x(n) by l units and compute rxy(l):
rxy = {r (−7), r (−6), r (−5), r (−4), r (−3), r (−2), r (−1), r (0)
↑
r (1), r (2), r (3), r (4), r (5), r (6), r (7)}
= {10, - 9, 19, 36, - 14, 33, 0, 7, 15, - 19, 19, 0, 6, - 1, - 3}
↑
Notes: In this case range of l is 0 to ±7; this means there are 2x7+1=15
elements in rxy.
February 3, 2013 A.H. 31

32. Similarities between computation of
Cross-correlation and convolution of 2
sequences
• Similarities are apparent
• Convolution computation- fold  shift  multiply one
sequence with the other to get the product sequence, and
then elements of the product sequence are summed to get
the conv. output.
• Cross-correlation computation – Same operations except the
folding one.
• rxy(l) = x(l) * y(-l) [See text]
February 3, 2013 A.H. 32

33. DSP Lecture
INTRODUCTION
THE END
THANK YOU
This ppt may be downloaded from my web site:
http://asadul.drivehq.com/students.htm
Password (email address): dsp.ete@ulab.edu.bd
This password does not live long !
Feb 3, 2013 A.H. 33