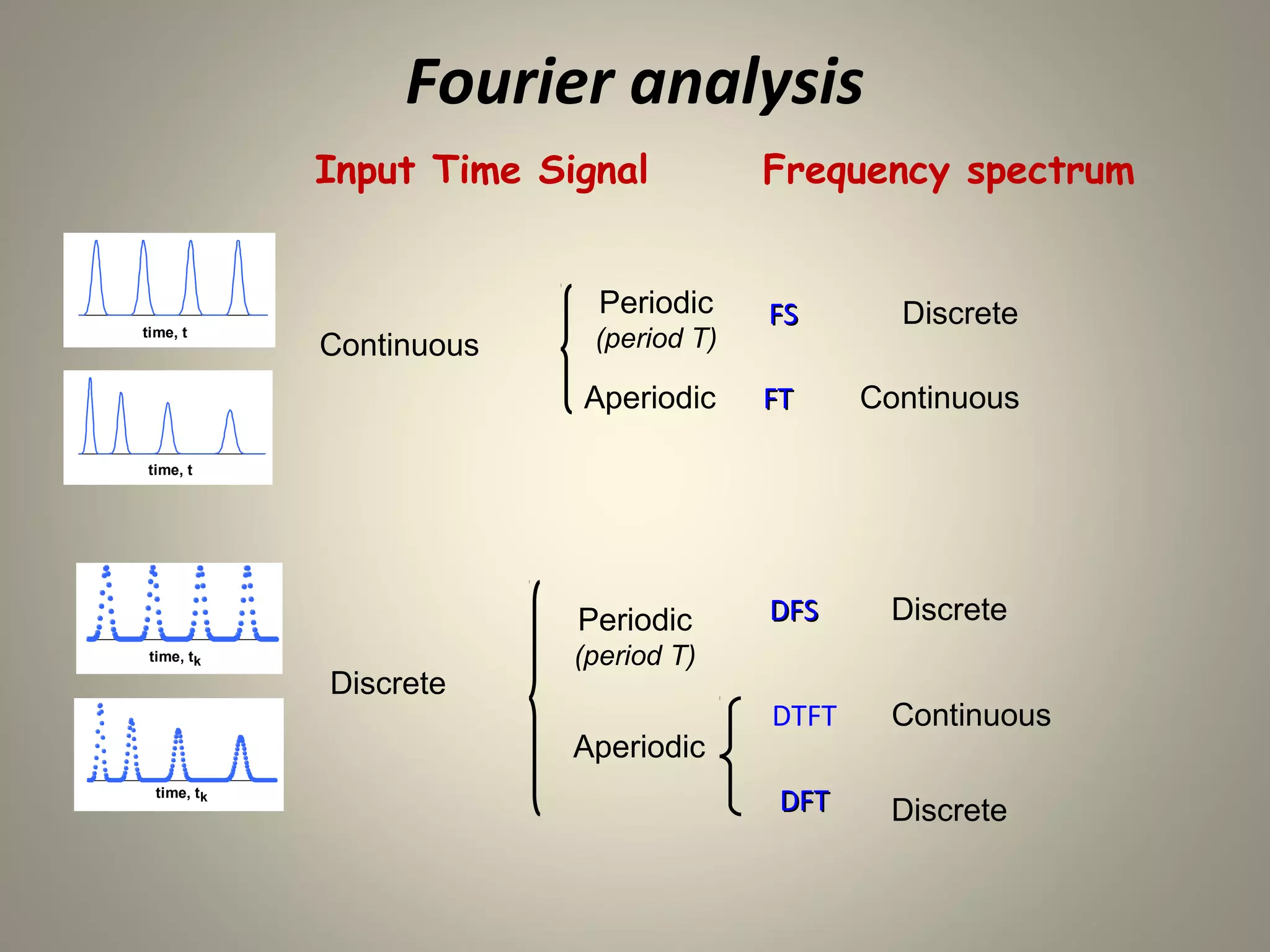
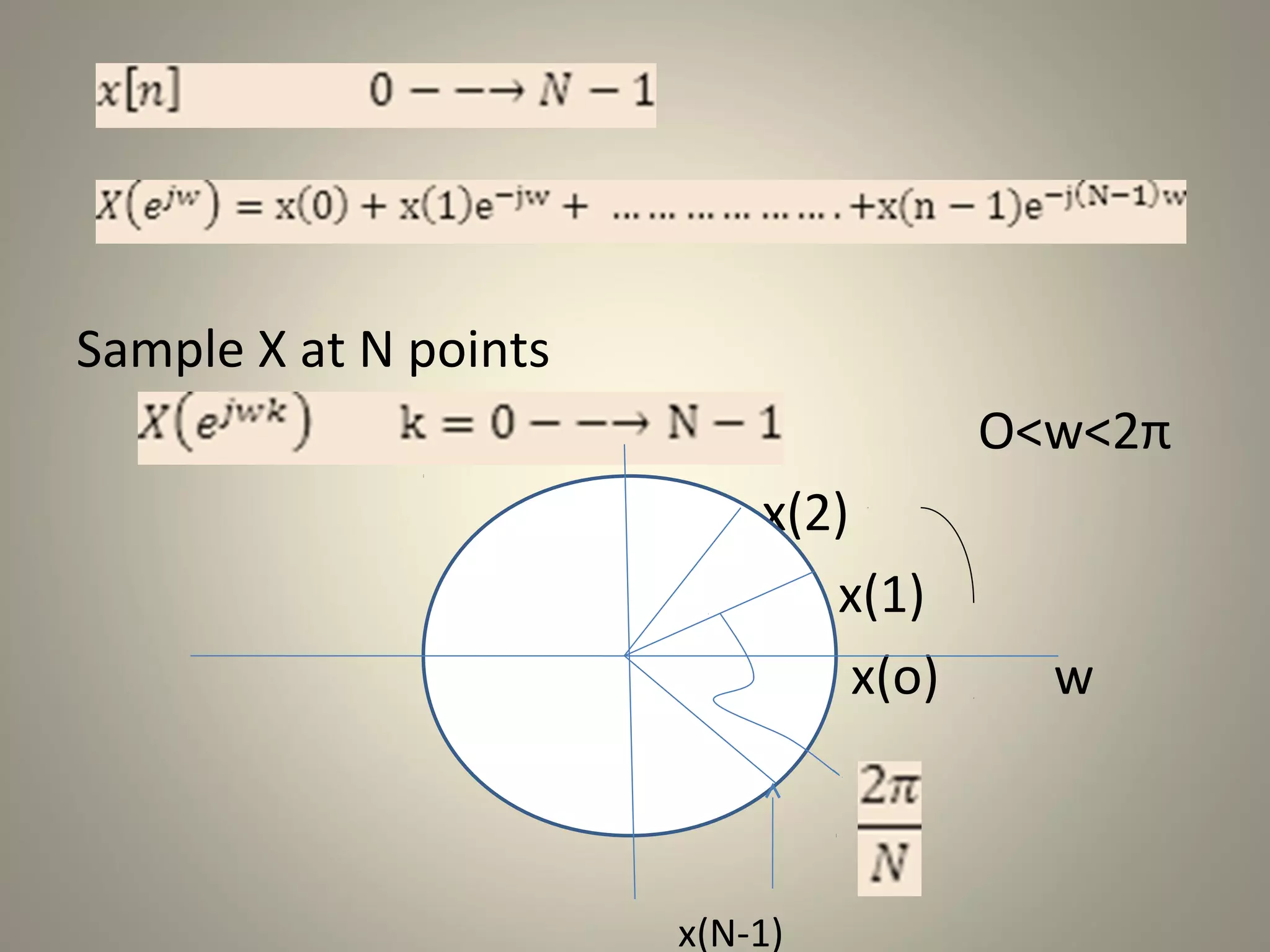
The document discusses the Discrete Fourier Transform (DFT). It begins by explaining the limitations of the Discrete Time Fourier Transform (DTFT) and Discrete Fourier Series (DFS) from a numerical computation perspective. It then introduces the DFT as a numerically computable transform obtained by sampling the DTFT in the frequency domain. The DFT represents a periodic discrete-time signal using a sum of complex exponentials. It defines the DFT and inverse DFT equations. The document also discusses properties of the DFT such as linearity and time/frequency shifting. Finally, it notes that the Fast Fourier Transform (FFT) implements the DFT more efficiently by constraining the number of points to powers of two.

1. Discrete Fourier Transform
(DFT)
Presented by: SHAHRYAR ALI

2. Discrete Time FT (DTFT)
DTFT defined as: Note: continuous frequency domain!
(frequency density function)
s
si +∞
ly
na
a S(f) = ∑ s[n] ⋅ e − j 2 π f n
n = −∞ Holds for Aperiodic
signals
is
hes 2π
nt 1
sy s[n] = ⋅ ∫ S(f)e j 2 π f ndf
2π
0

3. Problem With DTFT
– Defined for infinite-length sequences.
– From numerical computation viewpoint:
“It is troublesome as one has to evaluate infinite sums at
uncountable infinite frequencies”
– To use Matlab, we have to truncate sequences and then
evaluate the expression at many finite points.

4. Therefore:
• We turn our attention to a numerically computable
transform.
• It is obtained by sampling the DTFT transform in the
frequency domain (or the z-transform on the unit circle).
But..
• We know that a periodic function can always be
represented by:
“A linear combination of harmonically related complex
exponentials”

5. The Discrete Fourier Series
• So we have Discrete Fourier Series representation.
• Definition: Periodic sequence.
~ (n) = ~ (n + kN ), ∀n, k
x x
N: the fundamental period of the sequences

6. Discrete Fourier Series
Analysis equation:
~ N −1
~[n]e − j( 2 π / N)kn
X[k ] = ∑x
n=0
Synthesis equation:
~[n] = 1 N −1 ~
x ∑ X[k ]e j( 2 π / N)kn
N k =0

7. • For convenience we sometimes use:
− j( 2 π / N )
WN = e
So..
~ N −1
~[n]Wkn
X[k ] = ∑x N
n=0
~
{ X ( K ), k = 0,±1, } called the discrete Fourier series
are
coefficients.
~[n] = 1
N −1
~
x ∑ X[k ]WN kn
−
N k =0

8. Properties of DFS
• Linearity
~ [n] ~
x1 ← DFS →
  X1 [k ]
~ [n] ~
x 2 ← DFS →
  X2 [k ]
~ ~
a~1 [n] + b~2 [n]
x x ← DFS → aX1 [k ] + bX2 [k ]
 
• Shift of a Sequence
~[n] ~
x ← DFS →
 X[k ]
~
X[n] ← DFS → N~[ − k ]
 x
• Duality
~[n] ~
x DFS
←  →
 X[k ]
~[n − m] ~
x ←  → e − j2 πkm / NX[k ]
DFS

e j2 πnm / N~
x [n] ← → ~[k − m]
DFS
 X

9. The Fourier Transform of Periodic Signals
• Periodic sequences are not absolute or square summable
– Hence they don’t have a Fourier Transform.
• We can represent them as sums of complex exponentials:
DFS.
• We can define a periodic signal whose primary shape is
that of the finite duration signal .
• We then use the DFS on this periodic signal.
• So we define a new transform called the Discrete Fourier
Transform (DFT), which is the primary Period of the DFS.

10. Discrete Fourier Transform (DFT)

11. Discrete Fourier Transform (DFT)
• Discrete Fourier transform (or DFT) takes a finite number
of samples of a signal.
• It then transforms them into a finite number of
frequency samples .
• The discrete Fourier transform does not act on signals
that exist at all time.
• The DFT can be used in practice using a fast Fourier
transform (FFT) algorithm.

12. Fourier analysis
Input Time Signal Frequency spectrum
2.5
2
1.5
1
0.5
0
0 1 2 3 4 5 6 7 8
Periodic FS Discrete
time, t
Continuous (period T)
2.5
2
1.5 Aperiodic FT Continuous
1
0.5
0
0 2 4 6 8 10 12
time, t
2.5
2
DFS Discrete
1.5
Periodic
1
0.5
0
(period T)
0 1 2 3 4 5 6 7 8
time, tk
Discrete
DTFT Continuous
2.5
2
Aperiodic
1.5
1
0.5
0
time, tk
DFT
0 2 4 6 8 10 12
Discrete

13. Discrete Fourier Transform (DFT)
Definition: The Discrete Fourier Transform (DFT) is defined by:
Where n = 0, 1, 2, …., N-1
The Inverse Discrete Fourier Transform (IDFT) is defined by:
where k = 0, 1, 2, …., N-1.
Same form of DFS but for aperiodic signals.
Signal treated as periodic for computational purpose only.

14. Sample X at N points
O<w<2π
x(2)
x(1)
x(o) w
x(N-1)

15. DFT at work
• To see how DFT equation actually works in practice,
let’s do a simple example - calculate DFT of 4
element sequence, x(n)={1,1,0,0}
for k=0
4−1
X ( 0 ) = ∑ x ( n ) e− j 2π ×0×n 4
n= 0
= x ( 0 ) e − j 2π ×0×0 4 + x ( 1) e − j 2π ×0×1 4 + x ( 2 ) e− j 2π ×0×2 4 + x ( 3) e − j 2π ×0×3 4
= 1×e− j 2π ×0×0 4 + 1×e− j 2π ×0×1 4 + 0 ×e − j 2π ×0×2 4 + 0 ×e− j 2π ×0×3 4
=2

16. DFT at work
for k=1
X ( 1) = x ( 0 ) e − j 2π ××0 4 + x ( 1) e − j 2π ×× 4 + x ( 2 ) e − j 2π ××2 4 + x ( 3) e − j 2π ××3 4
1 11 1 1
= 1×e − j 2π ××0 4 + 1 ×e − j 2π ×× 4 + 0 ×e − j 2π ××2 4 + 0 ×e − j 2π ××3 4
1 11 1 1
 π   π 
= 1 +  cos  ÷− j sin  ÷÷
 2  2 
= 1− j
• Following the same procedure we also get:
X ( 2) = 0 X ( 3) = 1 + j
• The result: DFT({1,1,0,0})={2,1+j,0,1-j}

17. DFT Properties
Time Frequency
Linearity a·s[n] + b·u[n] a·S(k)+b·U(k)
1 N−1
Multiplication s[n] ·u[n] ⋅ ∑S(h)U(k - h)
N h =0
N− 1
Convolution S(k)·U(k)
∑ s[m] ⋅ u[n − m]
m= 0
Time shifting s[n - m]
2π k ⋅m
−j
e T ⋅ S(k)
Frequency shifting S(k - h)
2π h t
+j
e T ⋅ s[n]

18. s[n]
S(f)
(a) (b)
0 T/2 T 2T f
s”[n] IDFT
DFT
(c) (d)
(e)
(f) cK
(a) Aperiodic discrete signal. (b) DTFT transform magnitude.
(c) Periodic version of (a). (d) DFS coefficients = samples of (b).
(e) Inverse DFT estimates a single period of s[n]
(f) DFT estimates a single period of (d).

19. Why DFT is important?
 To find the frequency content of a signal.
• To design an audio format (e.g., CD audio).
• To design a communications system (what bandwidth is
required?).
 To determine the frequency response of a structure.
• A musical instrument.

20. The Fast Fourier Transform
• The fast Fourier transform (FFT) is simply a class of
special algorithms which implement the discrete Fourier
transform .
• It calculates with considerable savings in computational
time.
• Maximum efficiency of computation is obtained by
constraining the points to be an integer power of two,
e.g. 1024 or 2048.

21. QUESTIONS???