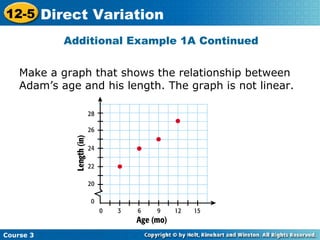
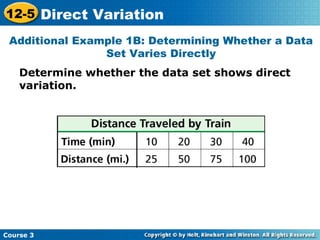
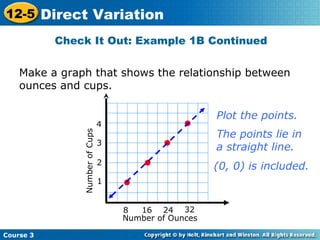
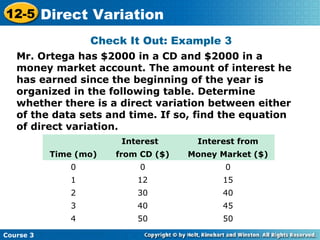
This document is a lesson on direct variation from a mathematics course. It begins with warm up problems identifying points and slopes of lines from their equations. It then covers identifying direct variation by graphing data and checking if ratios are constant. It provides examples of determining if data sets show direct variation and finding equations of direct variation given points. It concludes with a lesson quiz testing finding equations of direct variation from points and determining if data sets vary directly.

1. 12-5 Direct Variation
Course 3
Warm UpWarm Up
Problem of the DayProblem of the Day
Lesson PresentationLesson Presentation

2. Warm Up
Use the point-slope form of each
equation to identify a point the line
passes through and the slope of the
line.
1. y – 3 = – (x – 9)
2. y + 2 = (x – 5)
3. y – 9 = –2(x + 4)
4. y – 5 = – (x + 7)
(–4, 9), –2
Course 3
12-5 Direct Variation
1
7
2
3
1
4
(9, 3), –
1
7
(5, –2),
2
3
(–7, 5), – 1
4

3. Problem of the Day
Where do the lines defined by the
equations y = –5x + 20 and y = 5x – 20
intersect?
(4, 0)
Course 3
12-5 Direct Variation

4. Learn to recognize direct variation by
graphing tables of data and checking for
constant ratios.
Course 3
12-5 Direct Variation

5. Vocabulary
direct variation
constant of proportionality
Insert Lesson Title Here
Course 3
12-5 Direct Variation

6. Course 3
12-5 Direct Variation

7. Course 3
12-5 Direct Variation
The graph of a direct-variation equation is always
linear and always contains the point (0, 0). The
variables x and y either increase together or
decrease together.
Helpful Hint

8. Determine whether the data set shows direct
variation.
Additional Example 1A: Determining Whether a Data
Set Varies Directly
Course 3
12-5 Direct Variation

9. Make a graph that shows the relationship between
Adam’s age and his length. The graph is not linear.
Additional Example 1A Continued
Course 3
12-5 Direct Variation

10. You can also compare ratios to see if a direct
variation occurs.
22
3
27
12=
?
81
264
81 ≠ 264
The ratios are not proportional.
The relationship of the data is not a direct
variation.
Additional Example 1A Continued
Course 3
12-5 Direct Variation

11. Determine whether the data set shows direct
variation.
Additional Example 1B: Determining Whether a Data
Set Varies Directly
Course 3
12-5 Direct Variation

12. Make a graph that shows the relationship between
the number of minutes and the distance the train
travels.
Additional Example 1B Continued
Plot the points.
The points lie in
a straight line.
Course 3
12-5 Direct Variation
(0, 0) is included.

13. You can also compare ratios to see if a direct
variation occurs.
The ratios are proportional. The relationship is
a direct variation.
25
10
50
20
75
30
100
40
= = =
Compare ratios.
Additional Example 1B Continued
Course 3
12-5 Direct Variation

14. Determine whether the data set shows direct
variation.
Check It Out: Example 1A
Kyle's Basketball Shots
Distance (ft) 20 30 40
Number of Baskets 5 3 0
Course 3
12-5 Direct Variation

15. Make a graph that shows the relationship between
number of baskets and distance. The graph is not
linear.
Check It Out: Example 1A Continued
NumberofBaskets
Distance (ft)
2
3
4
20 30 40
1
5
Course 3
12-5 Direct Variation

16. You can also compare ratios to see if a direct
variation occurs.
Check It Out: Example 1A Continued
5
20
3
30=
?
60
150
150 ≠ 60.
The ratios are not proportional.
The relationship of the data is not a direct
variation.
Course 3
12-5 Direct Variation

17. Determine whether the data set shows direct
variation.
Check It Out: Example 1B
Ounces in a Cup
Ounces (oz) 8 16 24 32
Cup (c) 1 2 3 4
Course 3
12-5 Direct Variation

18. Make a graph that shows the relationship between
ounces and cups.
Check It Out: Example 1B Continued
NumberofCups
Number of Ounces
2
3
4
8 16 24
1
32
Course 3
12-5 Direct Variation
Plot the points.
The points lie in
a straight line.
(0, 0) is included.

19. You can also compare ratios to see if a direct
variation occurs.
Check It Out: Example 1B Continued
Course 3
12-5 Direct Variation
The ratios are proportional. The relationship is
a direct variation.
Compare ratios.
=
1
8
= =
2
16
3
24
4
32

20. Find each equation of direct variation, given
that y varies directly with x.
y is 54 when x is 6
Additional Example 2A: Finding Equations of Direct
Variation
y = kx
54 = k 
6
9 = k
y = 9x
y varies directly with x.
Substitute for x and y.
Solve for k.
Substitute 9 for k in the original
equation.
Course 3
12-5 Direct Variation

21. x is 12 when y is 15
Additional Example 2B: Finding Equations of Direct
Variation
y = kx
15 = k 
12
y varies directly with x.
Substitute for x and y.
Solve for k.= k5
4
Substitute for k in the original
equation.
5
4y = x
5
4
Course 3
12-5 Direct Variation

22. Find each equation of direct variation, given
that y varies directly with x.
y is 24 when x is 4
Check It Out: Example 2A
y = kx
24 = k 
4
6 = k
y = 6x
y varies directly with x.
Substitute for x and y.
Solve for k.
Substitute 6 for k in the original
equation.
Course 3
12-5 Direct Variation

23. x is 28 when y is 14
Check It Out: Example 2B
y = kx
14 = k 
28
y varies directly with x.
Substitute for x and y.
Solve for k.= k1
2
Substitute for k in the original
equation.
1
2y = x
1
2
Course 3
12-5 Direct Variation

24. Mrs. Perez has $4000 in a CD and $4000 in a
money market account. The amount of interest
she has earned since the beginning of the year
is organized in the following table. Determine
whether there is a direct variation between
either of the data sets and time. If so, find the
equation of direct variation.
Additional Example 3: Money Application
Course 3
12-5 Direct Variation

25. Additional Example 3 Continued
interest from CD and time
interest from CD
time
=
17
1
= = 17
interest from CD
time
34
2
The second and third pairs of data result in a common
ratio. In fact, all of the nonzero interest from CD to
time ratios are equivalent to 17.
The variables are related by a constant ratio of 17 to
1, and (0, 0) is included. The equation of direct
variation is y = 17x, where x is the time, y is the
interest from the CD, and 17 is the constant of
proportionality.
= = = 17
interest from CD
time
= =
17
1
34
2
51
3
68
4
Course 3
12-5 Direct Variation

26. Additional Example 3 Continued
interest from money market and time
interest from money market
time
= = 1919
1
interest from money market
time
= =18.537
2
19 ≠ 18.5
If any of the ratios are not equal, then there
is no direct variation. It is not necessary to
compute additional ratios or to determine
whether (0, 0) is included.
Course 3
12-5 Direct Variation

27. Mr. Ortega has $2000 in a CD and $2000 in a
money market account. The amount of interest he
has earned since the beginning of the year is
organized in the following table. Determine
whether there is a direct variation between either
of the data sets and time. If so, find the equation
of direct variation.
Check It Out: Example 3
Course 3
12-5 Direct Variation
Interest Interest from
Time (mo) from CD ($) Money Market ($)
0 0 0
1 12 15
2 30 40
3 40 45
4 50 50

28. Check It Out: Example 3 Continued
interest from CD
time
=
12
1
interest from CD
time
= = 15
30
2
The second and third pairs of data do not result in a
common ratio.
If any of the ratios are not equal, then there
is no direct variation. It is not necessary to
compute additional ratios or to determine
whether (0, 0) is included.
A. interest from CD and time
Course 3
12-5 Direct Variation

29. Check It Out: Example 3 Continued
B. interest from money market and time
interest from money market
time
= = 1515
1
interest from money market
time
= =2040
2
15 ≠ 20
If any of the ratios are not equal, then there
is no direct variation. It is not necessary to
compute additional ratios or to determine
whether (0, 0) is included.
Course 3
12-5 Direct Variation

30. Lesson Quiz: Part I
Find each equation of direct variation, given
that y varies directly with x.
1. y is 78 when x is 3.
2. x is 45 when y is 5.
3. y is 6 when x is 5.
y = 26x
Insert Lesson Title Here
y = x1
9
y = x6
5
Course 3
12-5 Direct Variation

31. Lesson Quiz: Part II
4. The table shows the amount of money Bob
makes for different amounts of time he works.
Determine whether there is a direct variation
between the two sets of data. If so, find the
equation of direct variation.
Insert Lesson Title Here
direct variation; y = 12x
Course 3
12-5 Direct Variation