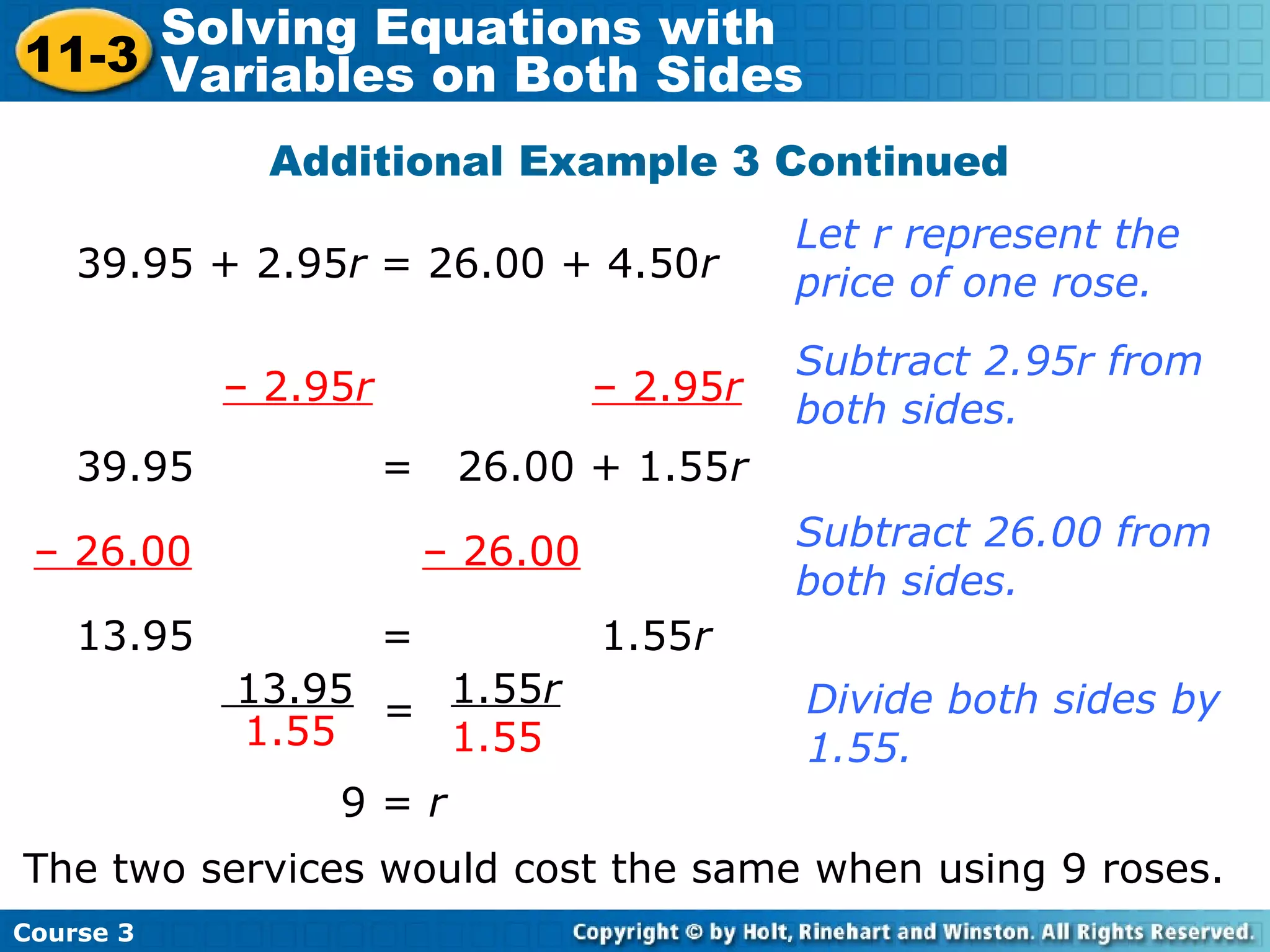
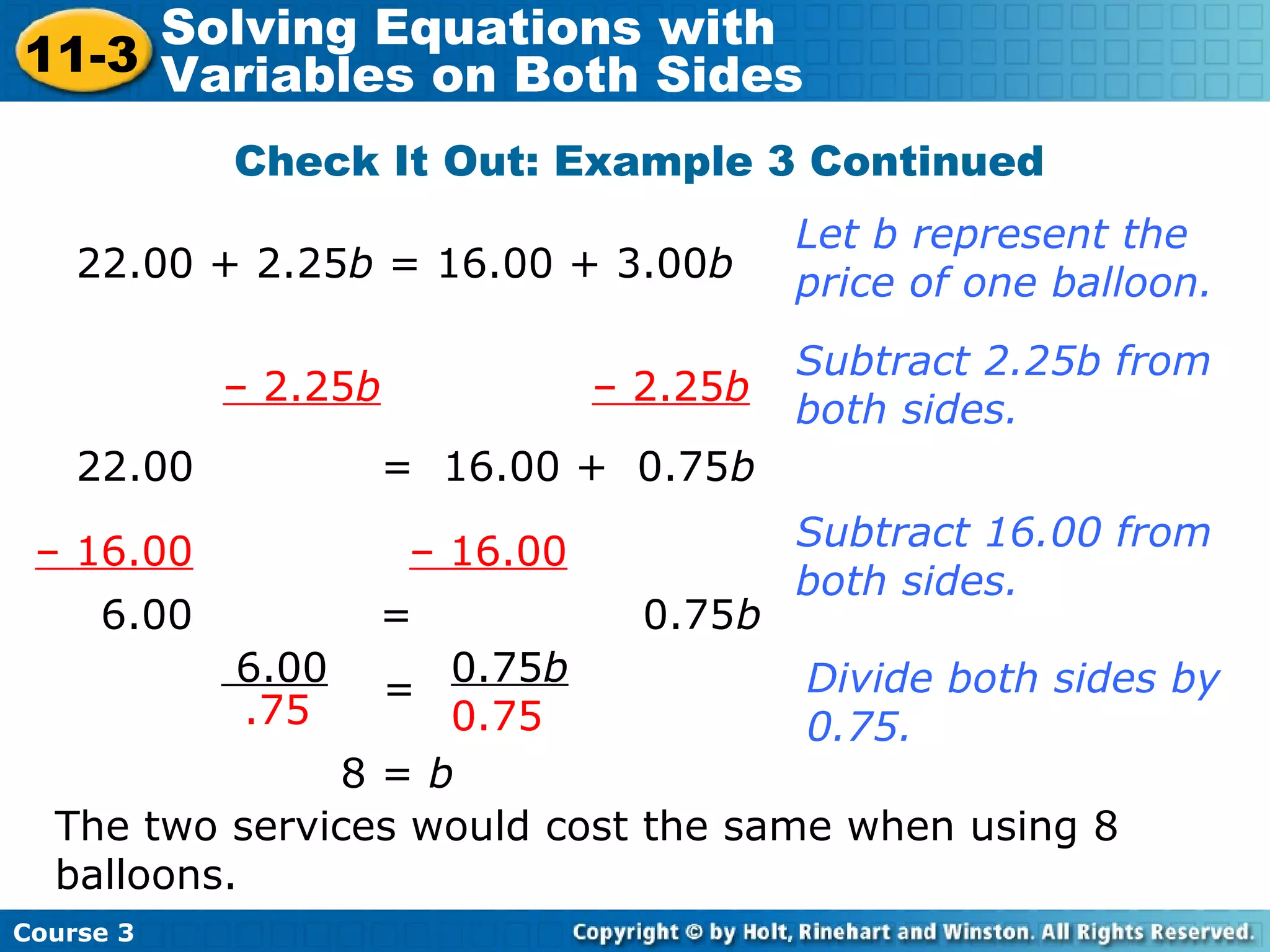
This document is a lesson on solving equations with variables on both sides of the equal sign. It begins with examples of solving single-step equations with variables on both sides through adding or subtracting terms. It then covers solving multi-step equations, including examples with business applications involving roses, balloons, and doughnuts. The document concludes with a lesson quiz to check understanding.

1. 11-3
Solving Equations with
Variables on Both Sides
Course 3
Warm UpWarm Up
Problem of the DayProblem of the Day
Lesson PresentationLesson Presentation

2. Warm Up
Solve.
1. 2x + 9x – 3x + 8 = 16
2. –4 = 6x + 22 – 4x
3. + = 5
4. – = 3
x = 1
x = -13
x = 34
Course 3
11-3
Solving Equations with
Variables on Both Sides
2
7
x
7 7
1
9x
16
2x
4
1
8
x = 50

3. Problem of the Day
An equilateral triangle and a regular
pentagon have the same perimeter.
Each side of the pentagon is 3 inches
shorter than each side of the triangle.
What is the perimeter of the triangle?
22.5 in.
Course 3
11-3
Solving Equations with
Variables on Both Sides

4. Learn to solve equations with variables on
both sides of the equal sign.
Course 3
11-3
Solving Equations with
Variables on Both Sides

5. Some problems produce equations that have
variables on both sides of the equal sign.
Solving an equation with variables on both
sides is similar to solving an equation with a
variable on only one side. You can add or
subtract a term containing a variable on both
sides of an equation.
Course 3
11-3
Solving Equations with
Variables on Both Sides

6. Solve.
4x + 6 = x
Additional Example 1A: Solving Equations with
Variables on Both Sides
4x + 6 = x
– 4x – 4x
6 = –3x
Subtract 4x from both sides.
Divide both sides by –3.
–2 = x
6
–3
–3x
–3=
Course 3
11-3
Solving Equations with
Variables on Both Sides

7. Course 3
11-3
Solving Equations with
Variables on Both Sides
Check your solution by substituting the value
back into the original equation. For example,
4(−2) + 6 = −2 or −2 = −2.
Helpful Hint

8. Solve.
9b – 6 = 5b + 18
Additional Example 1B: Solving Equations with
Variables on Both Sides
9b – 6 = 5b + 18
– 5b – 5b
4b – 6 = 18
4b
4
24
4
=
Subtract 5b from both sides.
Divide both sides by 4.
b = 6
+ 6 + 6
4b = 24
Add 6 to both sides.
Course 3
11-3
Solving Equations with
Variables on Both Sides

9. Solve.
9w + 3 = 9w + 7
Additional Example 1C: Solving Equations with
Variables on Both Sides
3 ≠ 7
9w + 3 = 9w + 7
– 9w – 9w Subtract 9w from both sides.
No solution. There is no number that can be
substituted for the variable w to make the
equation true.
Course 3
11-3
Solving Equations with
Variables on Both Sides

10. Course 3
11-3
Solving Equations with
Variables on Both Sides
if the variables in an equation are eliminated
and the resulting statement is false, the
equation has no solution.
Helpful Hint

11. Solve.
5x + 8 = x
Check It Out: Example 1A
5x + 8 = x
– 5x – 5x
8 = –4x
Subtract 5x from both sides.
Divide both sides by –4.
–2 = x
8
–4
–4x
–4
=
Course 3
11-3
Solving Equations with
Variables on Both Sides

12. Solve.
3b – 2 = 2b + 12
3b – 2 = 2b + 12
– 2b – 2b
b – 2 = 12
Subtract 2b from both sides.
+ 2 + 2
b = 14
Add 2 to both sides.
Check It Out: Example 1B
Course 3
11-3
Solving Equations with
Variables on Both Sides

13. Solve.
3w + 1 = 3w + 8
1 ≠ 8
3w + 1 = 3w + 8
– 3w – 3w Subtract 3w from both sides.
No solution. There is no number that can be
substituted for the variable w to make the
equation true.
Check It Out: Example 1C
Course 3
11-3
Solving Equations with
Variables on Both Sides

14. To solve multi-step equations with variables on
both sides, first combine like terms and clear
fractions. Then add or subtract variable terms
to both sides so that the variable occurs on
only one side of the equation. Then use
properties of equality to isolate the variable.
Course 3
11-3
Solving Equations with
Variables on Both Sides

15. Solve.
10z – 15 – 4z = 8 – 2z - 15
Additional Example 2A: Solving Multi-Step Equations
with Variables on Both Sides
10z – 15 – 4z = 8 – 2z – 15
+ 15 +15
6z – 15 = –2z – 7 Combine like terms.
+ 2z + 2z Add 2z to both sides.
8z – 15 = – 7
8z = 8
z = 1
Add 15 to both sides.
Divide both sides by 8.
8z 8
8 8
=
Course 3
11-3
Solving Equations with
Variables on Both Sides

16. Additional Example 2B: Solving Multi-Step Equations
with Variables on Both Sides
Multiply by the LCD,
20.
4y + 12y – 15 = 20y – 14
16y – 15 = 20y – 14 Combine like terms.
y
5
3
4
3y
5
7
10
+ – = y –
y
5
3
4
3y
5
7
10
+ – = y –
20( ) = 20( )y
5
3
4
3y
5
7
10
+ – y –
20( ) + 20( ) – 20( )= 20(y) – 20( )y
5
3y
5
3
4
7
10
Course 3
11-3
Solving Equations with
Variables on Both Sides

17. Additional Example 2B Continued
Add 14 to both sides.
–15 = 4y – 14
–1 = 4y
+ 14 + 14
–1
4
4y
4
= Divide both sides by 4.
–1
4
= y
16y – 15 = 20y – 14
– 16y – 16y Subtract 16y from both
sides.
Course 3
11-3
Solving Equations with
Variables on Both Sides

18. Solve.
12z – 12 – 4z = 6 – 2z + 32
Check It Out: Example 2A
12z – 12 – 4z = 6 – 2z + 32
+ 12 +12
8z – 12 = –2z + 38 Combine like terms.
+ 2z + 2z Add 2z to both sides.
10z – 12 = 38
10z = 50
z = 5
Add 12 to both sides.
Divide both sides by 10.
10z 50
10 10
=
Course 3
11-3
Solving Equations with
Variables on Both Sides

19. Multiply by the LCD,
24.
6y + 20y + 18 = 24y – 18
26y + 18 = 24y – 18 Combine like terms.
y
4
3
4
5y
6
6
8
+ + = y –
y
4
3
4
5y
6
6
8
+ + = y –
24( ) = 24( )y
4
3
4
5y
6
6
8
+ + y –
24( ) + 24( )+ 24( )= 24(y) – 24( )y
4
5y
6
3
4
6
8
Check It Out: Example 2B
Course 3
11-3
Solving Equations with
Variables on Both Sides

20. Subtract 18 from both
sides.
2y + 18 = – 18
2y = –36
– 18 – 18
–36
2
2y
2
= Divide both sides by 2.
y = –18
26y + 18 = 24y – 18
– 24y – 24y Subtract 24y from both
sides.
Check It Out: Example 2B Continued
Course 3
11-3
Solving Equations with
Variables on Both Sides

21. Additional Example 3: Business Application
Daisy’s Flowers sell a rose bouquet for
$39.95 plus $2.95 for every rose. A
competing florist sells a similar bouquet
for $26.00 plus $4.50 for every rose. Find
the number of roses that would make both
florist’s bouquets cost the same price.
Course 3
11-3
Solving Equations with
Variables on Both Sides

22. Additional Example 3 Continued
39.95 + 2.95r = 26.00 + 4.50r
Let r represent the
price of one rose.
– 2.95r – 2.95r
39.95 = 26.00 + 1.55r
Subtract 2.95r from
both sides.
– 26.00 – 26.00 Subtract 26.00 from
both sides.
13.95 = 1.55r
13.95
1.55
1.55r
1.55
= Divide both sides by
1.55.
9 = r
The two services would cost the same when using 9 roses.
Course 3
11-3
Solving Equations with
Variables on Both Sides

23. Check It Out: Example 3
Marla’s Gift Baskets sell a muffin basket
for $22.00 plus $2.25 for every balloon. A
competing service sells a similar muffin
basket for $16.00 plus $3.00 for every
balloon. Find the number of balloons that
would make both gift basket companies
muffin baskets cost the same price.
Course 3
11-3
Solving Equations with
Variables on Both Sides

24. Check It Out: Example 3 Continued
22.00 + 2.25b = 16.00 + 3.00b
Let b represent the
price of one balloon.
– 2.25b – 2.25b
22.00 = 16.00 + 0.75b
Subtract 2.25b from
both sides.
– 16.00 – 16.00 Subtract 16.00 from
both sides.
6.00 = 0.75b
6.00
.75
0.75b
0.75
= Divide both sides by
0.75.
8 = b
The two services would cost the same when using 8
balloons.
Course 3
11-3
Solving Equations with
Variables on Both Sides

25. Additional Example 4: Multi-Step Application
Jamie spends the same amount of
money each morning. On Sunday, he
bought a newspaper for $1.25 and also
bought two doughnuts. On Monday, he
bought a newspaper for fifty cents and
bought five doughnuts. On Tuesday, he
spent the same amount of money and
bought just doughnuts. How many
doughnuts did he buy on Tuesday?
Course 3
11-3
Solving Equations with
Variables on Both Sides

26. Additional Example 4 Continued
First solve for the price of one doughnut.
1.25 + 2d = 0.50 + 5d
Let d represent the price
of one doughnut.
– 2d – 2d
1.25 = 0.50 + 3d
Subtract 2d from both sides.
– 0.50 – 0.50
Subtract 0.50 from both
sides.
0.75 = 3d
0.75
3
3d
3
= Divide both sides by 3.
0.25 = d
The price of one
doughnut is $0.25.
Course 3
11-3
Solving Equations with
Variables on Both Sides

27. Additional Example 4 Continued
Now find the amount of money Jamie spends each
morning.
1.25 + 2d
Choose one of the original
expressions.
Jamie spends $1.75 each
morning.
1.25 + 2(0.25) = 1.75
0.25n
0.25
1.75
0.25=
Let n represent the
number of doughnuts.
Find the number of doughnuts Jamie buys on Tuesday.
0.25n = 1.75
n = 7; Jamie bought 7 doughnuts on Tuesday.
Divide both sides by 0.25.
Course 3
11-3
Solving Equations with
Variables on Both Sides

28. Check It Out: Example 4
Helene walks the same distance every
day. On Tuesdays and Thursdays, she
walks 2 laps on the track, and then
walks 4 miles. On Mondays,
Wednesdays, and Fridays, she walks 4
laps on the track and then walks 2
miles. On Saturdays, she just walks
laps. How many laps does she walk on
Saturdays?
Course 3
11-3
Solving Equations with
Variables on Both Sides

29. Check It Out: Example 4 Continued
First solve for distance around the track.
2x + 4 = 4x + 2
Let x represent the distance
around the track.
– 2x – 2x
4 = 2x + 2
Subtract 2x from both sides.
– 2 – 2 Subtract 2 from both sides.
2 = 2x
2
2
2x
2= Divide both sides by 2.
1 = x
The track is 1 mile
around.
Course 3
11-3
Solving Equations with
Variables on Both Sides

30. Check It Out: Example 4 Continued
Now find the total distance Helene walks each day.
2x + 4 Choose one of the original
expressions.
Helene walks 6 miles each day.2(1) + 4 = 6
Let n represent the
number of 1-mile laps.
Find the number of laps Helene walks on Saturdays.
1n = 6
Helene walks 6 laps on Saturdays.
n = 6
Course 3
11-3
Solving Equations with
Variables on Both Sides

31. Lesson Quiz
Solve.
1. 4x + 16 = 2x
2. 8x – 3 = 15 + 5x
3. 2(3x + 11) = 6x + 4
4. x = x – 9
5. An apple has about 30 calories more than an
orange. Five oranges have about as many calories
as 3 apples. How many calories are in each?
x = 6
x = –8
Insert Lesson Title Here
no solution
x = 361
4
1
2
An orange has 45 calories. An apple
has 75 calories.
Course 3
11-3
Solving Equations with
Variables on Both Sides