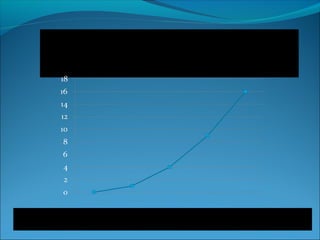
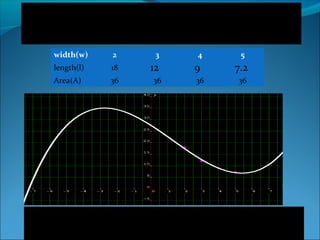
The document discusses different types of variations: 1) Direct variation results in a straight line graph, while direct square variation results in a parabolic graph. 2) Inverse variation means that as one variable increases, the other decreases, maintaining a constant product. The graph of an inverse variation is a hyperbola. 3) Examples show inverse variations between variables like pressure and volume of a gas, or jobs completed and number of workers. 4) Quiz questions test understanding of direct, inverse, and their equation representations.

1. REVIEW:
How does the graph of a direct
variation
look like?
The graph is a straight
line.

2. How does the graph of a direct square
variation
look like?
The graph is a curve line called parabola.

3. Read the ff. equations correctly.
1.) x = ky
2.) d = kf
3.) kw = j
4.) k = m
Direct Variation Direct Square Variation
n
5.) ky = z
1.) A = kd2
2.) R = kp2
3.) k = s
q2
4.) kg2 = h
5.) n = k
t2

4. Think of some real-life situations
wherein as one variable increases, the
other variable decreases or vice-versa.
Examples:
• As the number of trees decreases,
air pollution increases.
• As the speed of a car increases,
the length of travel time decreases.

5. Consider a rectangle whose area is 36 cm2. If the
width(w) is 2 cm, then its length(l) is 18 cm. What happens
when the width is increased to 3 cm? 4 cm?
width(w) 2 3 4 5
length(l) 18
Area(A) 36 36 36 36
12 9 7.2
The graph is neither a straight line nor a parabola
but a half of a two-part curve known as
hyperbola.

6. Lesson III:
Inverse Variation
Whenever the product of corresponding values of
two quantities is a constant, then one quantity varies
inversely as the other.
In symbols,
y = k(1) or y = k k = xy
x x
This means that y is inversely proportional to x, or x
is inversely proportional to y.

7. Examples:
A.For a given gas of constant temperature, the pressure(P) varies
inversely as the volume(V). If P = 6 when V = 24,
find P when V = 36.
P = k
V
k =PV 6 ?
= (6)(24) 24 36
= 144
= 144 = 4
36
B. Find the number of days 10 workers can complete a job if 5
workers can complete the same job in 7 days.
d = k
w
k =dw
= (7)(5)
= 35
= 35 = 3.5
10
5 10
7 ?

8. Read the equations below correctly.
I = k_
R
V =
k_
P
k = df
P = k_ gt = k
h

9. GROUP ACTIVITY:
Answer the following.
1.If y varies inversely as x, and y = 48
when x = 10, find y when x = 32
2. In the relation P1V1 = P2V2, P1 = 1.5 and
V1 = 24. Find V2 when P2 = 2.
3. For a given distance, the required
time(t) varies inversely as the rate R. If
t = 6 when R= 45 find R when t = 4 ½.
y = 15
V2 = 18
R = 60

10. QUIZ III
Write the ff. in equation form where k represent
the constant of variation.
1.The time(t) required to travel a given fixed distance is
inversely proportional to the speed(r).
2.The altitude(h) of a triangle with constant area varies
inversely as its base(b).
3.The temperature(T) at which water boils varies
inversely as the number of feet(h) above sea level.
Answer the following.
4.If c varies inversely as d and c = 30 when d = 9, find d
when c = 540.
5.The gravitational force(f) between two bodies varies
inversely as the square of distance(d) between them. Find
f when d = 5 and f = 100 when d = 4.
t = k
r
h = k
b
T = k
h
d = 1
2

11. Have a nice day………….
GOD
BLESS
YOU!!!