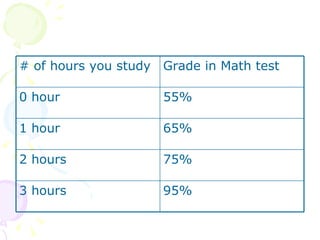
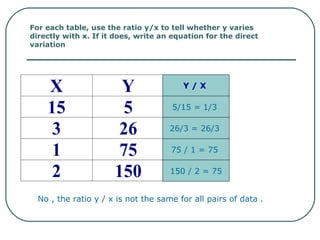
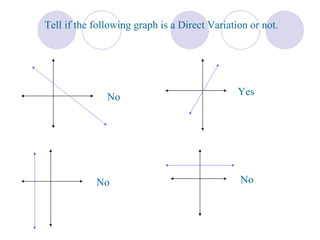
The document discusses direct variation, which is a relationship between two quantities where one quantity varies as the other changes such that they are proportional. It provides the definition of direct variation as y = kx, where k is the constant of variation. It gives examples of determining if an equation represents direct variation and writing an equation given a point. It also discusses using direct variation to find unknown values and illustrates direct variation through tables and graphs.

1. What do you guess? Eating too much Obesity

2. What do you guess? No studying Bad grade

3. 95% 3 hours 75% 2 hours 65% 1 hour 55% 0 hour Grade in Math test # of hours you study

4. What is it called when each of the variable increase the other increase?

5. Direct Variation I Math

6. OBJECTIVES Understand what is direct variation and the constant of variation. 2) Know how to solve problems with direct variation : + Is an equation a direct variation ? + Writing an equation given a point + Direct variations and tables + Direct variation and graph

7. Direct Variation What is it How can we know it ?

8. A direct variation is a function in the form y = kx where k does not equal 0. Definition

9. Y varies directly as x means that y = kx where k is the constant of variation. Another way of writing this is k = In other words: * the constant of variation (k) in a direct variation is the constant (unchanged) ratio of two variable quantities.( k = the coefficient of x ) NOTES

10. An equation is a direct variation if: its graph is a line that passes through zero, or the equation can be written in the form y = kx .

11. Problem solving

12. Is an equation a direct variation If it is, find the constant of variation

13. Example y – 7.5x = 0 y – 7.5x + 7.5x = 0 + 7.5 x Y = 7.5x Yes, it’s a direct variation. Constant of variable, k , is Solve for y 7.5

14. Practices 2y = 5x + 1 -12x = 6y

15. Writing an Equation Given a Point

16. Example y = kx Start with the function form of the direct variation. -3 = k(4) Substitute 4 for x and -3 for y. k= -3/4 Divide by 4 to solve for k. Substitute the value of k into the original formula. The Answer! Y= -3/4 x Write an equation of the direct variation that includes the point (4, -3).

17. Practices Write an equation of the direct variation that includes the point ( -3, -6 )

18. REAL WORLD PROBLEM SOLVING

19. Your distance from lightning varies directly with the time it takes you to hear thunder. If you hear thunder 10 seconds after you see the lightning, you are about 2 miles from the lightning. Write an equation for the relationship between time and distance

20. Relate: The distance varies directly with the time. When x = 10, y = 2. Define: Let x = number of seconds between seeing lightning and hearing thunder. Let y = distance in miles from lightning. y = kx ` Use general form of direct variation. 2 = k (10) Substitute 2 for y and 10 for x. ( Solve for k ) Write an equation using the value for k .

21. Direct Variation and tables

22. For each table, use the ratio y/x to tell whether y varies directly with x. If it does, write an equation for the direct variation Y / X 5/15 = 1/3 26/3 = 26/3 75 / 1 = 75 150 / 2 = 75 No , the ratio y / x is not the same for all pairs of data .

23. Which of the following is a direct variation? A B C D Answer Now

24. Which is the equation that describes the following table of values? y = -2x y = 2x y = ½ x xy = 200 Answer Now

25. Using Direct Variation to find unknowns (y = kx)

26. Given that y varies directly with x, and y = 28 when x=7, Find x when y = 52. HOW??? 2 step process 1. Find the constant variation k = y/x or k = 28/7 = 4 k=4 2. Use y = kx. Find the unknown (x). 52= 4x or 52/4 = x x= 13 Therefore: X =13 when Y=52

27. Practices Given that y varies directly with x, and y = 6 when x=-5, Find y when x = -8. HOW???

28. Given that y varies directly with x, and y = 6 when x=-5, Find y when x = -8. HOW??? 2 step process 1. Find the constant variation. k = y/x or k = 6/-5 = -1.2 k = -1.2 2. Use y = kx. Find the unknown (x). y= -1.2(-8) x= 9.6 Therefore: X =-8 when Y=9.6 Using Direct Variation to find unknowns (y = kx)

29. Direct Variation and its graph y = mx +b, m = slope and b = y-intercept With direction variation the equation is y = kx Note: m = k or the constant and b = 0 therefore the graph will always go through…

30. the ORIGIN!!!!!

31. Tell if the following graph is a Direct Variation or not. No Yes No No

32. GROUPS !!! With your group friends, come up with an interesting example that shows direct variation. ( 3 minutes ) FOR EXAMPLE : If you eat a lot , you will be fat

33. WHO IS FASTER ? 1 ) ONLY do the highlighted problems 2) You can do in pairs if you want 3) The 3 fastest people that finish all the problems with right answers will get the prize 1 st = 6 candies 2 nd = 4 candies 3 rd = 2 candies

34. HOMEWORK Finish the worksheet ( 3 , 4 , 6 , 7 , 9 , 10 , 11 , 12 )