The document presents an overview of digital image processing, discussing different types of digital images, such as binary, grayscale, and color images. Key methods in digital image processing include image enhancement, restoration, compression, and segmentation, focusing on techniques like intensity transformation and spatial filtering. Examples of transformations like negative and logarithmic transformations are provided to illustrate how they enhance image details.

1. Presented By,
J. Steffi
T. Navis
R. Gayathri
Manonmaniam Sundaranar University
Tirunelveli - 12
M.Phil. Computer Science
2017

2.  An image is a spatial representation of a two dimensional
or three dimensional scene.
 A digital image is composed of a finite number of
elements, each of which has a particular location and value.
 A digital image are classified into three types,
 Black/White or Binary image
 Gray-scale image
 Color/RGB image

3.  A digital image processing is a method to perform some
operations on an image, in order to get an enhanced image
or to extract some useful information from it.
 The digital image processing methods used in various
areas, such as :
 Medical imaging
 Astronomy
 Remote Earth resource observation

4.  The basic digital image processing methods are,
 Image Enhancement
 Image Restoration
 Image Compression
 Image Segmentation

5.  An Image Enhancement is the process of manipulating or
adjusting digital image so that the result is more suitable for
display or further image analysis.
 For example, you can remove noise, sharpen, smooth or
brighten an image, make it easier to identify key features.

6.  Image enhancement methods operate in,
• Spatial domain
- manipulating the pixel data
• Frequency domain
- modifying the spectral component
 Spatial domain refers to the image plane itself.
 Image processing methods in this category are based on
direct manipulation of pixels in an image.

7. (x,
y)
3 x 3 neighborhood of
(x, y)
Image
f
Spatial
domain
pixel (x,
y)
4-neighbors of pixel (x,
y)
8-neighbors of pixel (x,
y)
&

8.  A 3 x 3 neighborhood about a point ( x, y ) in an image in
the spatial domain.
 The neighborhood is moved from pixel to pixel in the image
to generate an output image.
(x,
y)
3 x 3 neighborhood of
(x, y)
Image
f
Spatial
domain

9.  Two principal categories of spatial domain processing are
• Intensity Transformation
• Spatial Filtering
 Intensity transformation operate on single pixels of an
image, principally for the purpose of contrast manipulation
and image threshold.
 Spatial filtering deals with performing operations, such as
image sharpening, by working in a neighborhood of every
pixel in an image.

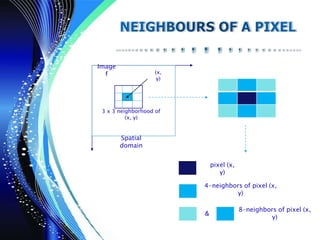
10.  The spatial domain process can be denoted by the expression,
g ( x, y ) = T [ f ( x, y ) ]
 Here,
 x and y are spatial ( plane ) coordinates
 ( x, y ) is the intensity/gray level the image at that point
 f ( x, y ) is the input image
 g ( x, y ) is the output image
 T is an operator

11.  The point processing is a simple method of image
enhancement.
 The point processing technique, which results depend only
on the intensity at a point.
 This point processing function of the form
s = T ( r )
 Here,
 s refers to the processed image
 r refers to the original image
 T is a transformation that maps a pixel value r into a
pixel value s

12.  The point processing function is also called as intensity
transformation or gray - level mapping function.
 The point processing functions can be further categorized
into two types.
 They are as follow :
 Linear Functions
 Non – Linear Functions

13.  Linear intensity transformation functions
• The negative transformation functions
• The identity transformation functions
 Non – linear transformation functions
 The Logarithmic
• log transformation functions
• inverse log transformation functions
 The Power – law
• nth power transformation functions
• nth root transformation functions

14. Basic intensity transformation functions

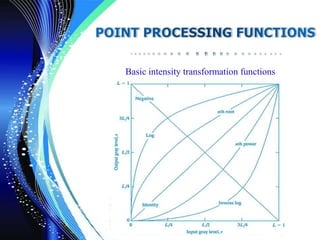
15.  The negative of an image with intensity levels in the range
[0, L-1] is obtained by using the negative transformation.
 The negative transformation is given by the following expression,
s = ( L - 1 ) – r
 s is a negative image
 L has a maximum gray level range of values 0 to 255
 r is an original gray-scale image
 Reversing the intensity levels of an image in this manner
produces the equivalent of photographic negative.
 This type of processing is particularly suited for enhancing white
or gray detail embedded in dark regions of an image.

16. Gray – Scale
Image
Negative
Image
Example for image negative transformation

17.  The general form of the log transformation is,
s = c log ( 1 + r )
where, c is constant, and it is assumed that r >= 0.
 The log transformation maps a narrow range of low input
gray level values into a wider range of output values.
 The inverse log transformation performs the opposite
transformation.

18.  The shape of the log curve in image shows that the log
transformation,

19.  Log functions are particularly useful when the input
gray level values may have an extremely large range
of values.
 The following example shows the result of applying
the log transform into a gray-scale image is used to
reveal more detail.

20. Gray – Scale
Image
Result of applying the log
transformation with c = 1
Example for log transformation

21.  The power-law transformation is also called as gamma
transformation.
 The power-law transformation have the following form
s = c r γ
 where c and γ are positive constants and plots of s versus
r for various values of γ.
 In power-law transformation, power-law curves with
fractional values of γ map a narrow range of dark input
values into a wide range of output values.

22. Plots of the equation s = crγ for various values of γ
(c = 1 in all cases)

23. Example for power-law transformation
Aerial Image Gamma Corrected
Image with γ = 5. 0