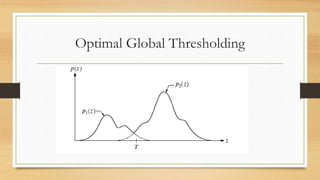
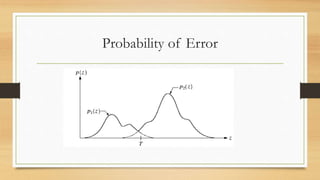
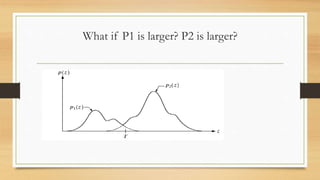
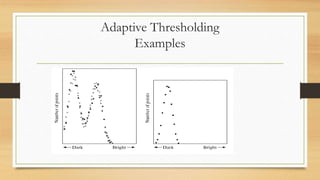
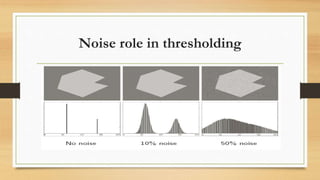
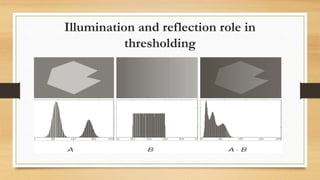
The document discusses different methods of thresholding for image segmentation. It begins by introducing thresholding as a simple segmentation technique that separates pixels into binary regions based on intensity values. It then describes several types of thresholding including global, variable, local/regional, and adaptive thresholding. The document also discusses challenges of thresholding, such as not considering pixel relationships, and methods for choosing optimal threshold values including analyzing the image histogram and using Otsu's method to maximize inter-class variance. It concludes by introducing local and adaptive thresholding techniques to address issues with uneven illumination.

1. THRESHOLDING
PRESENTED BY
R.RAMADEVI
M.sc(CS & IT)
NADAR SARASWATHI COLLEGE OF ARTS &
SCIENCE
THENI

2. Introduction
 Segmentation involves separating an image into regions (or their
contours)corresponding to objects.
 We usually try to segment regions by identifying common properties. Or,
similarly,
We identify contours by identifying differences between regions
(edges).
The simplest property that pixels in a region can share is intensity.

3. • Thresholding creates binary images from grey-level ones by turning all
pixels
• below some threshold to zero and all pixels about that threshold to one. If
g(x, y) is a thresholded version of f (x, y) at some global threshold T.
• g is equal to 1 if f (x, y) ≥ T and zero otherwise.
Problems with Thresholding
• The major problem with thresholding is that we consider only the
intensity, not any
• relationships between the pixels. There is no guarantee that the pixels
identified by the thresholding process are contiguous.

4. Segmentation by thresholding
• Thresholding is the simplest segmentation method.
• I The pixels are partitioned depending on their intensity value.
• I Global thresholding, using an appropriate threshold T:
• g(x, y) ={1, if f (x, y) > T
0, if f (x, y) T
Variable thresholding, if T can change over the image.
• I Local or regional thresholding, if T depends on a
• neighborhood of (x, y).
• I adaptive thresholding, if T is a function of (x, y).

5. • Variable thresholding, if T can change over the image.
• Local or regional thresholding, if T depends on a neighborhood of (x, y).
• adaptive thresholding, if T is a function of (x, y).
• Multiple thresholding:
g(x,y) ={a, if f(x,y)>t1
b, ift1<f(x,y)<t2
c, iff(x,y)<t1

6. FOUNDATION

7. Choosing the thresholds
• Peaks and valleys of the image histogram can help in choosing the appropriate value for
the threshold(s).
• Some factors affects the suitability of the histogram for guiding the choice of the
threshold:
The separation between peaks;
The noise content in the image;
The relative size of objects and background;
The uniformity of the illumination;
The uniformity of the reflectance.

8. Noise role in thresholding

9. Illumination and reflection role in
thresholding

10. Global thresholding
• A simple algorithm:
1. Initial estimate of T
2. Segmentation using T:
• G1, pixels brighter than T;
• G2, pixels darker than (or equal to) T.
3. Computation of the average intensities m1 and m2 of G1 and
• G2.
• New threshold value:
Tnew =m1 + m2
2

11. Global thresholding: an example

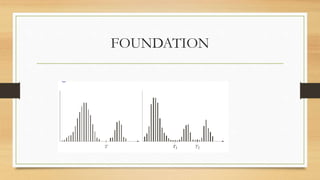
12. Otsu’s method
• Otsu’s method is aimed in finding the optimal value for the global
threshold.
• It is based on the interclass variance maximization.
• Well thresholded classes have well discriminated intensity values.
• M × N image histogram:
• L intensity levels, [0, . . . , L − 1];
• ni #pixels of intensity i :

13. Optimal Global Thresholding
A threshold is said to be globally optimal if the number of misclassified
pixels is minimum
 Histogram is bimodal (object and background)
 Ground truth is known OR the histograms of the object and the
background are known

14. Optimal Global Thresholding

15. Optimal Global Thresholding
• If the individual (normalized) histograms are known as p1(z) and p2(z)
• The (normalized) histogram of the overall image is
• P1p1(z)+P2p2(z) where P1=N1/(N1+N2) and P2=N2/(N1+N2)
• Notice that P1+P2=1

16. Probability of Error

17. Probability of Error
• Probability of erroneously classifying a class 1 pixel to
• class 2 is
• E (T)=∫∞ p (z)dz 2 1
• Probability of erroneously classifying a class 2 pixel to
• class 1 is
• E (T)=∫ −∞ p (z)dz
• Overall probability of error is then
• E(T)=P2E1(T)+P1E2(T)

18. Minimization of Probability of Error
• Let E’(T)=0 we have P1p1(T)=P2p2(T)
• If p1(T), p2(T) are known, T can be determined
• If P1=P2 (# of object pixels = # of background pixels), the optimum T is
where the curves intersect

19. What if P1 is larger? P2 is larger?

20. A Special Case
• An analytical expression for T is available if both normalized histograms
can be modeled as Gaussian distributions
• T must satisfy the quadratic equation Parameter Estimation
• Parameters involved in an assumed functional form can be estimated
using a minimization of mean-square-error approach

21. Local Thresholding
• Another problem with global thresholding is that changes in illumination
across the scene may cause some parts to be brighter (in the light) and
some parts darker (in shadow) in ways that have nothing to do with the
objects in the image.
• We can deal, at least in part, with such uneven illumination by determining
thresholds locally. That is, instead of having a single global threshold, we
allow the threshold itself to smoothly vary across the image.

22. Hysteresis Thresholding
• Take into account neighbors.
• 1. Choose two thresholds and high T low T
• 2. If T > Thigh the pixel is in the body. If low T < T the pixel is in the
background.
• 3. If the pixel is in the body only if a neighbor is already in the body low
high T < T < T
• 4. Iterate

23. Automated Methods for Finding
Thresholds
• To set a global threshold or to adapt a local threshold to an area, we usually look
at the histogram to see if we can find two or more distinct modes—one for the
foreground and one for the background.
• Recall that a histogram is a probability distribution:
• p(g)=ng /n
• That is, the number of pixels ng having grayscale intensity g as a fraction of the
total number of pixels n. Here are five different ways to look at the problem:

24. Adaptive Thresholding

25. Adaptive Thresholding
• One way to overcome the uneven illumination problem is to first estimate
the uneven illumination and then correct it accordingly (rectification)
• Another way is to use adaptive thresholding by partition the original
image into several subimages and utilize global thresholding techniques
for each subimage

26. Adaptive Thresholding Examples

27. Adaptive Thresholding
Examples

28. Adaptive Thresholding
Examples

29. Adaptive Thresholding
Examples
• Major procedures used for this example
• – Dividing the image into subimages
– Testing for bimodality for each subimage
– Apply Optimal Global
• Thresholding for each identified image with bimodal histogram

30. THANK YOU!