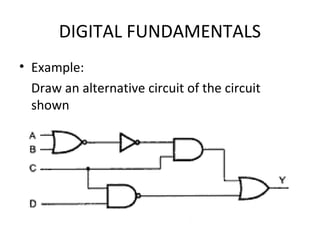
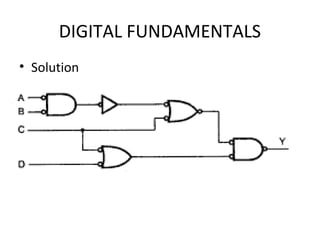
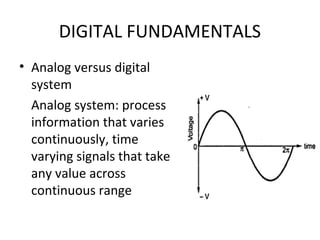
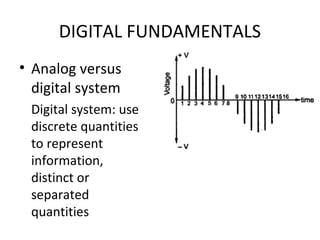
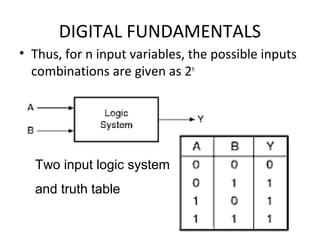
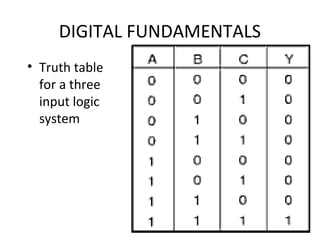
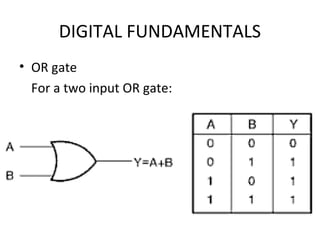
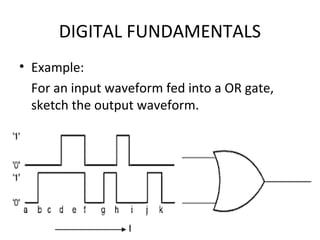
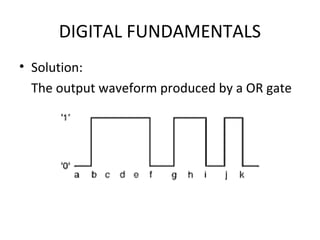
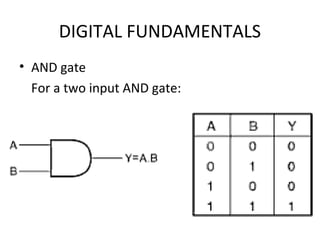
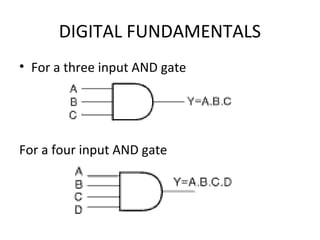
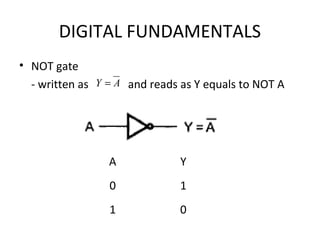
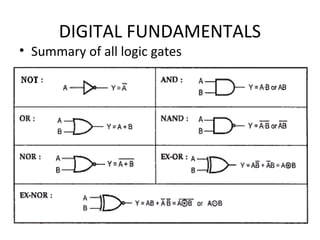
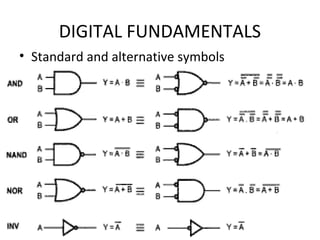
This document discusses digital electronics fundamentals including: - The difference between analog and digital systems, with digital systems using discrete quantities to represent information. - Logic levels assume two values (HIGH or LOW) to represent binary digits. Logic families define characteristics for compatible digital circuits. - Truth tables list all input-output combinations for logic gates like AND, OR, and NOT, which are basic building blocks of digital systems. Boolean algebra can simplify logic expressions.

1. DIGITAL ELECTRONICS
CHAPTER 2
DEE 204

2. DIGITAL ELECTRONICS
Digital fundamentals
Difference between analog and digital
systems.
Logic levels and families.
Logic values, truth tables and logical
operations.
Boolean algebra.
De Morgan’s Theorem

3. DIGITAL FUNDAMENTALS
• Analog versus digital
system
Analog system: process
information that varies
continuously, time
varying signals that take
any value across
continuous range

4. DIGITAL FUNDAMENTALS
• Analog versus
digital system
Digital system: use
discrete quantities
to represent
information,
distinct or
separated
quantities

5. DIGITAL FUNDAMENTALS
• Advantages of digital system:
– ease of design
– reproducibility of result
– flexibility
– functionality
– programmability
– speed
– economy

6. DIGITAL FUNDAMENTALS
• Logic levels
Binary logic used in digital system assumes
only TWO values: HIGH or LOW
These two levels or states can represent
two numerals: 1 and 0 of the binary system or
two logic states: TRUE and FALSE of the logic
operations

7. DIGITAL FUNDAMENTALS
• Logic family
- fundamental approach used to produce
different types of digital integrated circuit
- different logic functions belonging to the
same logic family will have identical
electrical characteristics: supply voltage
range, speed of response, power
dissipation, input and output logic levels,
current sourcing and sinking capability,
etc., making it compatible with each other

8. DIGITAL FUNDAMENTALS
• Types of logic families:
1. Bipolar – diode logic (DL), resistor
transistor logic (RTL), diode transistor
logic (DTL), transistor transistor logic
(TTL), emitter couple logic (ECL), current
mode logic (CML), integrated injection
logic (IIL or I2
L)
2. MOS – PMOS, NMOS, CMOS
3. Bi-MOS – using both bipolar and MOS

9. DIGITAL FUNDAMENTALS
• Binary variables have either logic ‘0’ state or
logic ‘1’ state which usually represents two
different voltage or current levels
• It may be a more positive(1) or less positive
(0) value referred as positive logic system
• Or may be the more positive (0) and less
positive (1) referred as negative logic system

10. DIGITAL FUNDAMENTALS
• Example:
A positive logic system for values 0V and +5V
0V = 0, +5V = 1
A negative logic system for values 0V and +5V
0V = 1, +5V = 0

11. DIGITAL FUNDAMENTALS
• Example:
A positive logic system for 0V and -5V
0V = 1, -5V = 0
A negative logic system for 0V and -5V
0V = 0, -5V = 1

12. DIGITAL FUNDAMENTALS
• Truth table
- lists all possible combinations of input binary
variables and the corresponding outputs of a
logic system
- depends on the number of binary input
variables; one will have two possibilities, two
will have four possibilities, while 3 will have 8
possibilities

13. DIGITAL FUNDAMENTALS
• Thus, for n input variables, the possible inputs
combinations are given as 2n
Two input logic system
and truth table

14. DIGITAL FUNDAMENTALS
• Truth table
for a three
input logic
system

15. DIGITAL FUNDAMENTALS
• Logic gates
- most basic building block of any digital
system
- a piece of hardware or an electronic circuit
used to implement basic logic expression
- the three basic logic gates are OR gate, AND
gate and NOT gate

16. DIGITAL FUNDAMENTALS
• OR gate
- to perform OR operation for two or
more logic variables with two or more
inputs and one output
- written as Y = A + B (Y equals to A OR B)
- output of OR gate is LOW when all inputs
are LOW and HIGH for any other input
combinations

17. DIGITAL FUNDAMENTALS
• OR gate
For a two input OR gate:

18. DIGITAL FUNDAMENTALS
• Example:
For an input waveform fed into a OR gate,
sketch the output waveform.

19. DIGITAL FUNDAMENTALS
• Solution:
The output waveform produced by a OR gate

20. DIGITAL FUNDAMENTALS
• AND gate
- also with two or more inputs and one output
- the output is HIGH when all inputs are HIGH
and LOW for any other combinations
- the output will become ‘1’ only when all
inputs are ‘1’
- written as Y = A.B (Y equals to A AND B)

21. DIGITAL FUNDAMENTALS
• AND gate
For a two input AND gate:

22. DIGITAL FUNDAMENTALS
• For a three input AND gate
For a four input AND gate

23. DIGITAL FUNDAMENTALS
• NOT gate
- a one input one output logic circuit which
complements the input
- the input is HIGH when the input is LOW and
vice versa
- a logic ‘0’ produces a logic ‘1’
- known as ‘complementing’ or ‘inverting’
circuit

24. DIGITAL FUNDAMENTALS
• NOT gate
- written as and reads as Y equals to NOT AAY =
A Y
0 1
1 0

25. DIGITAL FUNDAMENTALS
• Summary of all logic gates

26. DIGITAL FUNDAMENTALS
• Standard and alternative symbols

27. DIGITAL FUNDAMENTALS
• Example:
Draw an alternative circuit of the circuit
shown

28. DIGITAL FUNDAMENTALS
• Solution

29. DIGITAL FUNDAMENTALS
• Boolean algebra
- used to do manipulation of binary
variables and simplify logic expressions
- is basically the mathematics of logic
- composed of a set of symbols and a set
of rules to manipulate these symbols

30. DIGITAL FUNDAMENTALS
• Rules of Boolean algebra
1. A + 0 = A 7. A.A = A
2. A + 1 = 1 8.
3. A.0 = 0 9.
4. A.1 = A 10. A + AB = A
5. A + A = A 11.
6. 12. (A + B)(A + C) = A + BC1=+ AA
0. =AA
AA =
BABAA +=+

31. DIGITAL FUNDAMENTALS
• Boolean algebra
–There are cases when Boolean
algebra is used to simplify a Boolean
expression
–Simplification means fewer gates for
the same function

32. DIGITAL FUNDAMENTALS
• Example:
Simplify the given expression using Boolean algebra
techniques
( ) ( )CBBCBAAB ++++

33. DIGITAL FUNDAMENTALS
• Solution:
( ) ( )
ACB
BACAB
BCBACAB
BCBBACABAB
CBBCBAAB
+=
=+
++=
=+
+++=
=+=
++++=
++++
B)B(ABapplying
B)BC(Bapplying
AB)AB(ABandB)(BBapplying
givesequationtheexpanding

34. DIGITAL FUNDAMENTALS
• DeMorgan’s theorem
1. The complement of a product of variables is equal
to the sum of the complements of the variables
(The complement of two or more ANDed variables
is equivalent to the OR of the complements of each
variables)
2. The complement of a sum of variables is equivalent
to the product of the complements of the variables
(The complement of two or more ORed variables is
equivalent to the AND of the complements of each
variables)

35. DIGITAL FUNDAMENTALS
• DeMorgan’s theorem gives an expression
ZYXXYZ
YXYX
++=
=+ .

36. DIGITAL FUNDAMENTALS
• Example:
Apply DeMorgan’s theorem to the given expressions:
( )
EFDCBA
DEFABC
DCBA
++
+
++

37. DIGITAL FUNDAMENTALS
• Solution
( )
( )( ) ( )( )
( )( )( ) ( )( )( )FEDCBAEFDCBAEFDCBA
FEDCBADEFABCDEFABC
DCBADCBADCBA
+++==++
++++==+
+=+++=++ ..

38. DIGITAL FUNDAMENTALS
• Example:
Apply DeMorgan’s theorem to the given
expressions:
)ZY()YX(F +⋅⋅=1
ZYYXF
)ZY()YX(F
)ZY()YX(F
)ZY()YX(F
)ZY()YX(F
+=
⋅+⋅=
⋅+⋅=
++⋅=
+⋅⋅=
1
1
1
1
1

39. DIGITAL FUNDAMENTALS
• Example:
Apply DeMorgan’s theorem to the given
expressions:
YXZXF
)XY()ZX(F
)XY()ZX(F
)XY()ZX(F
)XY()ZX(F
)XY)(ZX(F
+=
+=
+=
++=
++=
+=
2
2
2
2
2
2